Im Vorfeld des Kursbeginns haben "Algorithmen für Entwickler" für Sie eine Übersetzung eines weiteren nützlichen Materials vorbereitet.
Die Huffman-Codierung ist ein Datenkomprimierungsalgorithmus, der die Grundidee der Dateikomprimierung formuliert. In diesem Artikel werden wir über Codierung mit fester und variabler Länge, eindeutig decodierte Codes, Präfixregeln und die Konstruktion eines Huffman-Baums sprechen.Wir wissen, dass jedes Zeichen als Folge von 0 und 1 gespeichert ist und 8 Bits benötigt. Dies wird als Codierung mit fester Länge bezeichnet, da jedes Zeichen dieselbe feste Anzahl von Bits zum Speichern verwendet.Nehmen wir an, der Text ist gegeben. Wie können wir den Speicherplatz reduzieren, der zum Speichern eines Zeichens erforderlich ist?Die Grundidee ist die Codierung mit variabler Länge. Wir können die Tatsache nutzen, dass einige Zeichen im Text häufiger vorkommen als andere ( siehe hier ), um einen Algorithmus zu entwickeln, der dieselbe Zeichenfolge mit weniger Bits darstellt. Beim Codieren einer variablen Länge weisen wir den Zeichen eine variable Anzahl von Bits zu, abhängig von der Häufigkeit ihres Auftretens in diesem Text. Letztendlich können einige Zeichen nur 1 Bit und andere 2 Bit, 3 oder mehr, aufnehmen. Das Problem bei der Codierung mit variabler Länge ist nur die nachfolgende Decodierung der Sequenz.Wie kann man die Reihenfolge der Bits kennen, um sie eindeutig zu dekodieren?Betrachten Sie die Zeichenfolge "aabacdab" . Es hat 8 Zeichen und beim Codieren einer festen Länge werden 64 Bit benötigt, um es zu speichern. Beachten Sie, dass die Häufigkeit der Zeichen "a", "b", "c" und "d" 4, 2, 1, 1 beträgt. Versuchen wir uns "aabacdab" mit weniger Bits vorzustellen, wobei wir die Tatsache verwenden, dass "a" häufiger als "b" und "b" häufiger als "c" und "d" ist . Zunächst codieren wir "a" mit einem Bit gleich 0, "b" weisen wir einen Zwei-Bit-Code 11 zu und codieren mit drei Bits 100 und 011 "c" und"D" .Als Ergebnis werden wir erfolgreich sein:Daher codieren wir die Zeichenfolge "aabacdab" unter Verwendung der oben angegebenen Codes als 00110100011011 (0 | 0 | 11 | 0 | 100 | 011 | 0 | 11) . Das Hauptproblem wird jedoch die Dekodierung sein. Wenn wir versuchen, die Zeile 00110100011011 zu dekodieren , erhalten wir ein mehrdeutiges Ergebnis, da es wie folgt dargestellt werden kann:0|011|0|100|011|0|11 adacdab
0|0|11|0|100|0|11|011 aabacabd
0|011|0|100|0|11|0|11 adacabab
...etc.Um diese Mehrdeutigkeit zu vermeiden, müssen wir sicherstellen, dass unsere Codierung einem Konzept wie einer Präfixregel entspricht , was wiederum impliziert, dass Codes auf nur eine eindeutige Weise decodiert werden können. Eine Präfixregel stellt sicher, dass kein Code ein Präfix eines anderen ist. Mit Code meinen wir Bits, die zur Darstellung eines bestimmten Zeichens verwendet werden. Im obigen Beispiel ist 0 das Präfix 011 , das gegen die Präfixregel verstößt. Wenn unsere Codes die Präfixregel erfüllen, können wir sie eindeutig dekodieren (und umgekehrt).Sehen wir uns das obige Beispiel an. Dieses Mal werden wir die Zeichen "a", "b", "c" und "d" zuweisen. Codes, die die Präfixregel erfüllen.Bei Verwendung dieser Codierung wird die Zeichenfolge "aabacdab" als 00100100011010 (0 | 0 | 10 | 0 | 100 | 011 | 0 | 10) codiert . Und hier 00100100011010 können wir eindeutig dekodieren und zu unserer ursprünglichen Zeile „aabacdab“ zurückkehren .Huffman-Codierung
Nachdem wir die Codierung mit variabler Länge und eine Präfixregel herausgefunden haben, sprechen wir über die Huffman-Codierung.Die Methode basiert auf der Erstellung von Binärbäumen. Darin kann ein Knoten entweder endlich oder intern sein. Anfangs werden alle Knoten als Blätter (Blätter) betrachtet, die das Symbol selbst und sein Gewicht (dh die Häufigkeit des Auftretens) darstellen. Interne Knoten enthalten die Gewichtung des Zeichens und beziehen sich auf zwei untergeordnete Knoten. Nach allgemeiner Vereinbarung steht das Bit "0" für eine Verfolgung im linken Zweig und "1" für die rechte. In einem vollständigen Baum gibt es N Blätter und N-1 interne Knoten. Es wird empfohlen, beim Erstellen eines Huffman-Baums nicht verwendete Zeichen zu verwerfen, um Codes mit optimaler Länge zu erhalten.Wir werden die Prioritätswarteschlange verwenden, um den Huffman-Baum zu erstellen, wobei dem Knoten mit der niedrigsten Frequenz die höchste Priorität zugewiesen wird. Die Konstruktionsschritte werden nachfolgend beschrieben:- Erstellen Sie für jedes Zeichen einen Blattknoten und fügen Sie ihn der Prioritätswarteschlange hinzu.
- Gehen Sie wie folgt vor, während Sie für mehr als ein Blatt in der Schlange stehen:
- Entfernen Sie die beiden Knoten mit der höchsten Priorität (mit der niedrigsten Frequenz) aus der Warteschlange.
- Erstellen Sie einen neuen internen Knoten, in dem diese beiden Knoten Erben sind und die Häufigkeit des Auftretens der Summe der Häufigkeiten dieser beiden Knoten entspricht.
- Fügen Sie der Prioritätswarteschlange einen neuen Knoten hinzu.
- Der einzige verbleibende Knoten ist die Wurzel. Dadurch wird die Baumkonstruktion abgeschlossen.
Stellen Sie sich vor, wir haben einen Text, der nur aus den Zeichen "a", "b", "c", "d" und "e" besteht, und die Häufigkeit ihres Auftretens beträgt 15, 7, 6, 6 bzw. 5. Unten finden Sie Abbildungen, die die Schritte des Algorithmus widerspiegeln.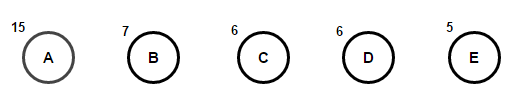
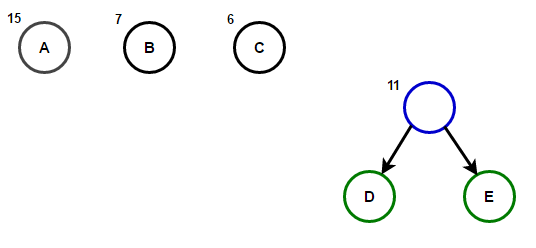
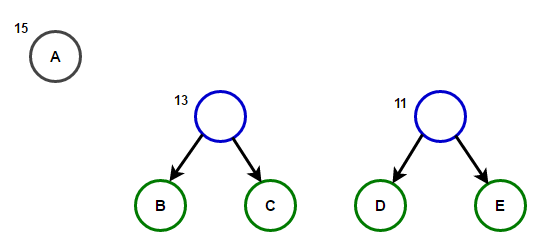
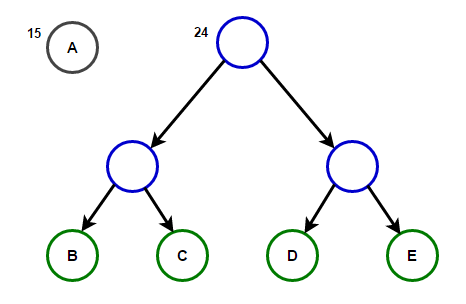
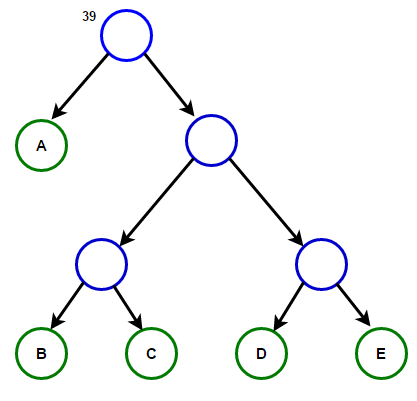 Der Pfad von der Wurzel zu einem beliebigen Endknoten speichert den optimalen Präfixcode (auch als Huffman-Code bezeichnet), der dem diesem Endknoten zugeordneten Zeichen entspricht.
Der Pfad von der Wurzel zu einem beliebigen Endknoten speichert den optimalen Präfixcode (auch als Huffman-Code bezeichnet), der dem diesem Endknoten zugeordneten Zeichen entspricht.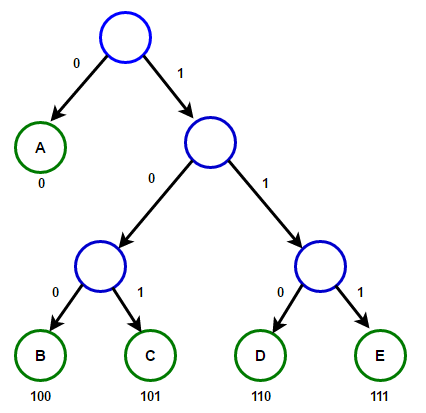 Huffman-BaumNachfolgend finden Sie die Implementierung des Huffman-Komprimierungsalgorithmus in C ++ und Java:
Huffman-BaumNachfolgend finden Sie die Implementierung des Huffman-Komprimierungsalgorithmus in C ++ und Java:#include <iostream>
#include <string>
#include <queue>
#include <unordered_map>
using namespace std;
struct Node
{
char ch;
int freq;
Node *left, *right;
};
Node* getNode(char ch, int freq, Node* left, Node* right)
{
Node* node = new Node();
node->ch = ch;
node->freq = freq;
node->left = left;
node->right = right;
return node;
}
struct comp
{
bool operator()(Node* l, Node* r)
{
return l->freq > r->freq;
}
};
void encode(Node* root, string str,
unordered_map<char, string> &huffmanCode)
{
if (root == nullptr)
return;
if (!root->left && !root->right) {
huffmanCode[root->ch] = str;
}
encode(root->left, str + "0", huffmanCode);
encode(root->right, str + "1", huffmanCode);
}
void decode(Node* root, int &index, string str)
{
if (root == nullptr) {
return;
}
if (!root->left && !root->right)
{
cout << root->ch;
return;
}
index++;
if (str[index] =='0')
decode(root->left, index, str);
else
decode(root->right, index, str);
}
void buildHuffmanTree(string text)
{
unordered_map<char, int> freq;
for (char ch: text) {
freq[ch]++;
}
priority_queue<Node*, vector<Node*>, comp> pq;
for (auto pair: freq) {
pq.push(getNode(pair.first, pair.second, nullptr, nullptr));
}
while (pq.size() != 1)
{
Node *left = pq.top(); pq.pop();
Node *right = pq.top(); pq.pop();
int sum = left->freq + right->freq;
pq.push(getNode('\0', sum, left, right));
}
Node* root = pq.top();
unordered_map<char, string> huffmanCode;
encode(root, "", huffmanCode);
cout << "Huffman Codes are :\n" << '\n';
for (auto pair: huffmanCode) {
cout << pair.first << " " << pair.second << '\n';
}
cout << "\nOriginal string was :\n" << text << '\n';
string str = "";
for (char ch: text) {
str += huffmanCode[ch];
}
cout << "\nEncoded string is :\n" << str << '\n';
int index = -1;
cout << "\nDecoded string is: \n";
while (index < (int)str.size() - 2) {
decode(root, index, str);
}
}
int main()
{
string text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
return 0;
}
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;
class Node
{
char ch;
int freq;
Node left = null, right = null;
Node(char ch, int freq)
{
this.ch = ch;
this.freq = freq;
}
public Node(char ch, int freq, Node left, Node right) {
this.ch = ch;
this.freq = freq;
this.left = left;
this.right = right;
}
};
class Huffman
{
public static void encode(Node root, String str,
Map<Character, String> huffmanCode)
{
if (root == null)
return;
if (root.left == null && root.right == null) {
huffmanCode.put(root.ch, str);
}
encode(root.left, str + "0", huffmanCode);
encode(root.right, str + "1", huffmanCode);
}
public static int decode(Node root, int index, StringBuilder sb)
{
if (root == null)
return index;
if (root.left == null && root.right == null)
{
System.out.print(root.ch);
return index;
}
index++;
if (sb.charAt(index) == '0')
index = decode(root.left, index, sb);
else
index = decode(root.right, index, sb);
return index;
}
public static void buildHuffmanTree(String text)
{
Map<Character, Integer> freq = new HashMap<>();
for (int i = 0 ; i < text.length(); i++) {
if (!freq.containsKey(text.charAt(i))) {
freq.put(text.charAt(i), 0);
}
freq.put(text.charAt(i), freq.get(text.charAt(i)) + 1);
}
PriorityQueue<Node> pq = new PriorityQueue<>(
(l, r) -> l.freq - r.freq);
for (Map.Entry<Character, Integer> entry : freq.entrySet()) {
pq.add(new Node(entry.getKey(), entry.getValue()));
}
while (pq.size() != 1)
{
Node left = pq.poll();
Node right = pq.poll();
int sum = left.freq + right.freq;
pq.add(new Node('\0', sum, left, right));
}
Node root = pq.peek();
Map<Character, String> huffmanCode = new HashMap<>();
encode(root, "", huffmanCode);
System.out.println("Huffman Codes are :\n");
for (Map.Entry<Character, String> entry : huffmanCode.entrySet()) {
System.out.println(entry.getKey() + " " + entry.getValue());
}
System.out.println("\nOriginal string was :\n" + text);
StringBuilder sb = new StringBuilder();
for (int i = 0 ; i < text.length(); i++) {
sb.append(huffmanCode.get(text.charAt(i)));
}
System.out.println("\nEncoded string is :\n" + sb);
int index = -1;
System.out.println("\nDecoded string is: \n");
while (index < sb.length() - 2) {
index = decode(root, index, sb);
}
}
public static void main(String[] args)
{
String text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
}
}
Hinweis: Der von der Eingabezeichenfolge verwendete Speicher beträgt 47 * 8 = 376 Bit, und die codierte Zeichenfolge benötigt nur 194 Bit, d. H. Daten werden um ca. 48% komprimiert. Im obigen C ++ - Programm verwenden wir die Zeichenfolgenklasse, um die codierte Zeichenfolge zu speichern und das Programm lesbar zu machen.Da effektive Datenstrukturen der Prioritätswarteschlange das Einfügen von O (log (N)) Zeit erfordern und in einem vollständigen Binärbaum mit N Blättern 2N-1 Knoten vorhanden sind und der Huffman-Baum ein vollständiger Binärbaum ist, arbeitet der Algorithmus für O (Nlog (N) )) Zeit, wobei N die Anzahl der Zeichen ist.Quellen:
en.wikipedia.org/wiki/Huffman_codingen.wikipedia.org/wiki/Variable-length_codewww.youtube.com/watch?v=5wRPin4oxCo
.