Kommt Ihnen das bekannt vor: "Ich habe nach dem Besuch der Kurse mit der Webentwicklung begonnen"?Vielleicht möchten Sie Ihre Kenntnisse der Grundlagen der Informatik in Bezug auf Datenstrukturen und Algorithmen verbessern. Heute werden wir anhand des JS-Beispiels über einige der häufigsten Datenstrukturen sprechen.1. Stapel (Aufrufe) (Stapel)
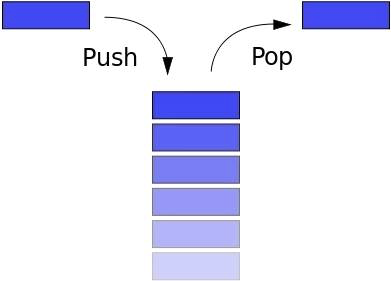Der Stack folgt dem LIFO-Prinzip (Last In First Out - Last In, First Out). Wenn Sie die Bücher übereinander gestapelt haben und das niedrigste Buch nehmen möchten, nehmen Sie zuerst das oberste, dann das nächste usw. Mit der Schaltfläche "Zurück" im Browser können Sie zur vorherigen Seite zurückkehren.Der Stapel verfügt über die folgenden Methoden:- push: Neues Element hinzufügen
- pop: oberes Element entfernen, zurückgeben
- Peek: Rückgabe des oberen Elements
- Länge: Gibt die Anzahl der Elemente auf dem Stapel zurück
Ein Array in JS hat Stapelattribute, aber wir werden es mit der Funktion Stack () von Grund auf neu erstellen:function Stack() {
this.count = 0
this.storage = {}
this.push = function(value) {
this.storage[this.count] = value
this.count++
}
this.pop = function() {
if (this.count === 0) return undefined
this.count--
let result = this.storage[this.count]
delete this.storage[this.count]
return result
}
this.peek = function() {
return this.storage[this.count - 1]
}
this.size = function() {
return this.count
}
}
2. Warteschlange (Warteschlange)
Eine Warteschlange ähnelt einem Stapel. Der Unterschied besteht darin, dass die Warteschlange dem FIFO-Prinzip folgt (First In First Out - First In, First Out). Wenn Sie in der Schlange stehen, ist der erste immer der erste.Die Warteschlange verfügt über die folgenden Methoden:- Warteschlange: Geben Sie die Warteschlange ein und fügen Sie am Ende ein Element hinzu
- Warteschlange: Verlassen Sie die Warteschlange, löschen Sie das erste Element und geben Sie es zurück
- vorne: Holen Sie sich das erste Element
- isEmpty: Überprüfen Sie, ob die Warteschlange leer ist
- Größe: Ermittelt die Anzahl der Elemente in der Warteschlange
Ein Array in JS hat einige Warteschlangenattribute, sodass wir es zur Demonstration verwenden können:function Queue() {
let collection = []
this.print = function() {
console.log(collection)
}
this.enqueue = function(element) {
collection.push(element)
}
this.dequeue = function() {
return collection.shift()
}
this.front = function() {
return collection[0]
}
this.isEmpty = function() {
return collection.length === 0
}
this.size = function() {
return collection.length
}
}
Die Reihenfolge der Priorität (Priorität)
Die Warteschlange hat eine erweiterte Version. Weisen Sie jedem Element eine Priorität zu, und die Elemente werden entsprechend sortiert:function PriorityQueue() {
...
this.enqueue = function(element) {
if (this.isEmpty()) {
collection.push(element)
} else {
let added = false
for (let i = 0; i < collection.length; i++) {
if (element[1] < collection[i][1]) {
collection.splice(i, 0, element)
added = true
break;
}
}
if (!added) {
collection.push(element)
}
}
}
}
Testen:let pQ = new PriorityQueue()
pQ.enqueue([gannicus, 3])
pQ.enqueue([spartacus, 1])
pQ.enqueue([crixus, 2])
pQ.enqueue([oenomaus, 4])
pQ.print()
Ergebnis:[
[spartacus, 1],
[crixus, 2],
[gannicus, 3],
[oenomaus, 4]
]
3. Eine verknüpfte Liste (verknüpfte Liste von Knoten und Verknüpfungen oder Zeigern) (verknüpfte Liste)
Eine verknüpfte Liste ist buchstäblich eine verkettete Datenstruktur, bei der jeder Knoten aus zwei Teilen besteht: Knotendaten und einem Zeiger auf den nächsten Knoten. Die verknüpfte Liste und das bedingte Array sind lineare Datenstrukturen mit serialisiertem Speicher. Die Unterschiede sind wie folgt:Eine einfach verknüpfte Liste verfügt über die folgenden Methoden:- Größe: Gibt die Anzahl der Knoten zurück
- Kopf: Rückgabe des ersten Elements (Kopf - Kopf)
- add: füge ein Element am Ende hinzu (tail - tail)
- Entfernen: Entfernen Sie mehrere Knoten
- indexOf: Rückgabeknotenindex
- elementAt: Rückgabeknoten nach Index
- addAt: Fügen Sie einen Knoten an einer bestimmten Stelle ein (nach Index).
- removeAt: Entfernen eines bestimmten Knotens (nach Index)
function Node(element) {
this.element = element
this.next = null
}
function LinkedList() {
let length = 0
let head = null
this.size = function() {
return length
}
this.head = function() {
return head
}
this.add = function(element) {
let node = new Node(element)
if (head === null) {
head = node
} else {
let currentNode = head
while (currentNode.next) {
currentNode = currentNode.next
}
currentNode.next = node
}
length++
}
this.remove = function(element) {
let currentNode = head
let previousNode
if (currentNode.element !== element) {
head = currentNode.next
} else {
while (currentNode.element !== element) {
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
}
this.isEmpty = function() {
return length === 0
}
this.indexOf = function(element) {
let currentNode = head
let index = -1
while (currentNode) {
index++
if (currentNode.element === element) {
return index
}
currentNode = currentNode.next
}
return -1
}
this.elementAt = function(index) {
let currentNode = head
let count = 0
while (count < index) {
count++
currentNode = currentNode.next
}
return currentNode.element
}
this.addAt = function(index, element) {
let node = new Node(element)
let currentNode = head
let previousNode
let currentIndex = 0
if (index > length) return false
if (index === 0) {
node.next = currentNode
head = node
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
node.next = currentNode
previousNode.next = node
}
length++
}
this.removeAt = function(index) {
let currentNode = head
let previousNode
let currentIndex = 0
if (index < 0 || index >= length) return null
if (index === 0) {
head = currentIndex.next
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
return currentNode.element
}
}
4. Sammlung (von Werten) (Set)
Eine Sammlung (viele) ist eines der Grundkonzepte der Mathematik: eine Reihe klar definierter und isolierter Objekte. ES6 führte eine Sammlung ein, die einem Array ähnelt. Die Sammlung erlaubt jedoch nicht die Aufnahme doppelter Elemente und enthält keine Indizes.Die Standardsammlung verfügt über die folgenden Methoden:- Werte: Gibt alle Elemente in der Sammlung zurück
- Größe: Gibt die Anzahl der Elemente zurück
- hat: Überprüfen Sie, ob sich ein Artikel in der Sammlung befindet
- Hinzufügen: Element hinzufügen
- entfernen: Einen Gegenstand entfernen
- union: Gibt den Schnittbereich zweier Sammlungen zurück
- Unterschied: Gibt die Unterschiede zwischen den beiden Sammlungen zurück
- Teilmenge: Überprüfen Sie, ob eine Sammlung eine Teilmenge einer anderen ist
function MySet() {
let collection = []
this.has = function(element) {
return (collection.indexOf(element) !== -1)
}
this.values = function() {
return collection
}
this.size = function() {
return collection.length
}
this.add = function(element) {
if (!this.has(element)) {
collection.push(element)
return true
}
return false
}
this.remove = function(element) {
if (this.has(element)) {
index = collection.indexOf(element)
collection.splice(index, 1)
return true
}
return false
}
this.union = function(otherSet) {
let unionSet = new MySet()
let firstSet = this.values()
let secondSet = otherSet.values()
firstSet.forEach(i => unionSet.add(i))
secondSet.forEach(i => unionSet.add(i))
}
this.intersection = function(otherSet) {
let intersectionSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (otherSet.has(e)) {
intersectionSet.add(e)
}
})
return intersectionSet
}
this.difference = function(otherSet) {
let differenceSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (!otherSet.has(e)) {
differenceSet.add(e)
}
})
return differenceSet
}
this.subset = function(otherSet) {
lat firstSet = this.values()
return firstSet.every(value => otherSet.has(value))
}
}
5. Hash-Tabelle (Hash-Tabelle)
Eine Hash-Tabelle ist eine Datenstruktur, die auf Schlüsselwertbasis erstellt wird. Aufgrund der hohen Geschwindigkeit bei der Suche nach Werten nach Schlüsseln wird es in Strukturen wie Map, Dictionary und Object verwendet. Wie in der Abbildung gezeigt, verfügt die Hash-Tabelle über eine Hash-Funktion, die Schlüssel in eine Liste von Zahlen konvertiert, die als Namen (Werte) von Schlüsseln verwendet werden. Die Schlüsselwertsuchzeit kann O (1) erreichen. Identische Schlüssel müssen denselben Wert zurückgeben - dies ist die Essenz der Hash-Funktion.Eine Hash-Tabelle hat die folgenden Methoden:- Hinzufügen: Fügen Sie ein Schlüssel / Wert-Paar hinzu
- Entfernen: Entfernen Sie ein Paar
- Nachschlagen: Wert anhand des Schlüssels finden
function hash(string, max) {
let hash = 0
for (let i = 0; i < string.length; i++) {
hash += string.charCodeAt(i)
}
return hash % max
}
function HashTable() {
let storage = []
const storageLimit = 4
this.add = function(key, value) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
storage[index] = [
[key, value]
]
} else {
let inserted = false
for (let i = 0; i < storage[index].len; i++) {
if (storage[index][i][0] === key) {
storage[index][i][1] = value
inserted = true
}
}
if (inserted === false) {
storage[index].push([key, value])
}
}
}
this.remove = function(key) {
let index = hash(key, storageLimit)
if (storage[index].length === 1 && storage[index][0][0] === key) {
delete storage[index]
} else {
for (let i = 0; i < storage[index]; i++) {
if (storage[index][i][0] === key) {
delete storage[index][i]
}
}
}
}
this.lookup = function(key) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
return undefined
} else {
for (let i = 0; i < storage[index].length; i++) {
if (storage[index][i][0] === key) {
return storage[index][i][1]
}
}
}
}
}
6. Baum
Eine Baumstruktur ist eine mehrschichtige Struktur. Es ist auch eine nichtlineare Struktur, im Gegensatz zu einem Array, einem Stapel und einer Warteschlange. Diese Struktur ist sehr effektiv beim Hinzufügen und Suchen von Elementen. Hier sind einige Konzepte der Baumstruktur:- root: root-Element, hat kein übergeordnetes Element
- übergeordneter Knoten: Ein direkter Knoten der obersten Ebene (Ebene), es kann nur einen geben
- untergeordneter Knoten: direkter Knoten der unteren Ebene, es können mehrere vorhanden sein
- Geschwister: Kinder eines Elternknotens
- Blatt: Knoten ohne "Kinder"
- Kante: Verzweigung oder Verknüpfung (Verknüpfung) zwischen Knoten
- Pfad: Pfad (Satz von Links) vom Startknoten zum Zielelement
- Baumhöhe: Die Anzahl der Verknüpfungen des längsten Pfads von einem bestimmten Element zu einem Knoten ohne untergeordnete Elemente
- Knotentiefe: Die Anzahl der Verknüpfungen vom Stammknoten zu einem bestimmten Element.
- Knotengrad: Anzahl der Nachkommen
Hier ist ein Beispiel für einen binären Suchbaum (BST). Jeder Knoten hat nur zwei Nachkommen, der linke (untergeordnete) Knoten ist kleiner als der aktuelle (übergeordnete) Knoten, der rechte ist größer: Die
Methoden dieses Baums sind wie folgt:- add: Knoten hinzufügen
- findMin: Minimalen Knoten abrufen
- findMax: Maximalen Knoten abrufen
- find: finde einen bestimmten Knoten
- isPresent: Suchen Sie nach einem bestimmten Knoten
- Entfernen: Entfernen Sie den Knoten
class Node {
constructor(data, left = null, right = null) {
this.data = data
this.left = left
this.right = right
}
}
class BST {
constructor() {
this.root = null
}
add(data) {
const node = this.root
if (node === null) {
this.root = new Node(data)
return
} else {
const searchTree = function(node) {
if (data < node.data) {
if (node.left === null) {
node.left = new Node(data)
return
} else if (node.left !== null) {
return searchTree(node.left)
}
} else if (data > node.data) {
if (node.right === null) {
node.right = new Node(data)
return
} else if (node.right !== null) {
return searchTree(node.right)
}
} else {
return null
}
}
return searchTree(node)
}
}
findMin() {
let current = this.root
while (current.left !== null) {
current = current.left
}
return current.data
}
findMax() {
let current = this.root
while (current.right !== null) {
current = current.right
}
return current.data
}
find(data) {
let current = this.root
while (current.data !== data) {
if (data < current.data) {
current = current.left
} else {
current = current.right
}
if (current === null) {
return null
}
}
return current
}
isPresent(data) {
let current = this.root
while (current) {
if (data === current.data) {
return true
}
data < current.data ? current = current.left : current = current.right
}
return false
}
remove(data) {
const removeNode = function(node, data) {
if (node === null) return null
if (data === node.data) {
if (node.left === null && node.right === null) return null
if (node.left === null) return node.right
if (node.right === null) return node.left
let tempNode = node.right
while (tempNode.left !== null) {
tempNode = tempNode.left
}
node.data = tempNode.data
node.right = removeNode(node.right, tempNode.data)
return node
} else if (data < node.data) {
node.left = removeNode(node.right, data)
return node
} else {
node.right = removeNode(node.right, data)
return node
}
}
this.root = removeNode(this.root, data)
}
}
Testen:const bst = new BST()
bst.add(4)
bst.add(2)
bst.add(6)
bst.add(1)
bst.add(3)
bst.add(5)
bst.add(7)
bst.remove(4)
console.log(bst.findMin())
console.log(bst.findMax())
bst.remove(7)
console.log(bst.findMax())
console.log(bst.isPresent(4))
Ergebnis:1
7
6
false
7. Geladener (Präfix-) Baum (Trie, gelesen als "try")
Der Präfixbaum ist eine Art Suchbaum. Die darin enthaltenen Daten werden nacheinander (Schritt für Schritt) gespeichert - jeder Baumknoten repräsentiert einen Schritt. Der Präfixbaum wird in Wörterbüchern verwendet, da er die Suche erheblich beschleunigt.Jeder Baumknoten ist ein Buchstabe des Alphabets. Wenn Sie einem Zweig folgen, entsteht ein Wort. Es enthält auch einen „Booleschen Indikator“, um festzustellen, ob der aktuelle Knoten der letzte Buchstabe ist.Der Präfixbaum verfügt über die folgenden Methoden:- Hinzufügen: Fügen Sie dem Wörterbuch ein Wort hinzu
- isWord: Suche nach einem Wort
- print: Alle Wörter zurückgeben
function Node() {
this.keys = new Map()
this.end = false
this.setEnd = function() {
this.end = true
}
this.isEnd = function() {
return this.end
}
}
function Trie() {
this.root = new Node()
this.add = function(input, node = this.root) {
if (input.length === 0) {
node.setEnd()
return
} else if (!node.keys.has(input[0])) {
node.keys.set(input[0], new Node())
return this.add(input.substr(1), node.key.get(input[0]))
} else {
return this.add(input.substr(1), node.keys.get(input[0]))
}
}
this.isWord = function(word) {
let node = this.root
while (word.length > 1) {
if (node.keys.has(word[0])) {
return false
} else {
node = node.keys.get(word[0])
word = word.substr(1)
}
}
return (node.keys.has(word) && node.keys.get(word).isEnd()) ? true : false
}
this.print = function() {
let words = new Array()
let search = function(node = this.root, string) {
if (node.keys.size !== 0) {
for (let letter of node.keys.keys()) {
search(node.keys.get(letter), string.concat(letter))
}
if (node.isEnd()) {
words.push(string)
}
} else {
string.length > 0 ? words.push(string) : undefined
return
}
}
search(this.root, new String())
return words.length > 0 ? words : null
}
}
8. Die Grafik (Grafik) (Grafik)
Ein Graph, auch als Netzwerk bezeichnet, ist eine Sammlung miteinander verbundener Knoten. Es gibt zwei Arten von Diagrammen - orientiert und nicht orientiert, je nachdem, ob die Links eine Richtung haben. Überall werden Grafiken verwendet, um beispielsweise die beste Route in Navigationsanwendungen zu berechnen oder eine Liste mit Empfehlungen in sozialen Netzwerken zu erstellen.Diagramme können in Form einer Liste oder Matrix dargestellt werden.Liste
In diesem Fall befinden sich alle übergeordneten Knoten links und ihre untergeordneten Knoten rechts.
Die Matrix
In diesem Fall sind die Knoten in Zeilen und Spalten verteilt, der Schnittpunkt von Zeile und Spalte zeigt die Beziehung zwischen den Knoten: 0 bedeutet, dass die Knoten nicht verbunden sind, 1 - die Knoten sind verbunden.
Das Diagramm wird mit zwei Methoden durchsucht: Breitensuche (Breath-First-Search, BFS) und Tiefensuche (Depth-First-Search, DFS).Betrachten Sie BFS:function bfs(graph, root) {
let nodesLen = {}
for (let i = 0; i < graph.length; i++) {
nodesLen[i] = Infinity
}
nodesLen[root] = 0
let queue = [root]
let current
while (queue.length !== 0) {
current = queue.shift()
let curConnected = graph[current]
let neighborIdx = []
let idx = curConnected.indexOf(1)
while (idx !== -1) {
neighborIdx.push(idx)
idx = curConnected.indexOf(1, idx + 1)
}
for (let i = 0; i < neighborIdx.length; i++) {
if (nodesLen[neighborIdx[i]] === Infinity) {
nodesLen[neighborIdx[i]] = nodesLen[current] + 1
queue.push(neighborIdx[i])
}
}
}
return nodesLen
}
Testen:let graph = [
[0, 1, 1, 1, 0],
[0, 0, 1, 0, 0],
[1, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 1, 0, 0, 0]
]
console.log(bfs(graph, 1))
Ergebnis:{
0: 2,
1: 0,
2: 1,
3: 3,
4: Infinity
}
Das ist alles für mich. Ich hoffe, Sie finden etwas Nützliches für sich. Viel Spaß beim Codieren!