Coderikeinmal bemerkt: "Es gibt nie zu viele Kalman-Filter . " Das Gleiche gilt für den Satz von Bayes, weil er einerseits so einfach ist, andererseits aber so schwer zu verstehen ist, wie tief er ist.

YouTube hat einen wunderbaren Student Dave- Kanal , aber das letzte Video wurde vor sechs Jahren gepostet. Der Kanal enthält Lehrvideos, in denen der Autor komplexe Dinge in einer sehr einfachen Sprache erzählt: Bayes-Theorem, Kalman-Filter usw. Student Dave ergänzt seine Geschichte mit einem Beispiel für die Berechnung in Matlab.

Einmal hat mir seine Videolektion mit dem Titel „Iterative Bayes'sche Bewertung“ sehr geholfen (auf dem Kanal entspricht sie der Wiedergabeliste „Iterative Bayes'sche Schätzung: mit MATLAB“).) Ich wollte, dass sich alle mit Daves Erklärungen vertraut machen, aber leider wird das Projekt nicht unterstützt. Dave selbst meldet sich nicht. Sie können dem Video keine Übersetzung hinzufügen, da der Autor sie selbst initiieren muss. Die Kontaktaufnahme mit youtube ergab kein Ergebnis, daher habe ich beschlossen, das Material in einem Artikel auf Russisch zu beschreiben und dort zu veröffentlichen, wo es am meisten geschätzt wird. Das Material wurde stark überarbeitet und ergänzt, da es meine subjektive Wahrnehmung durchlief, so dass es unangemessen wäre, es als Übersetzung zu verwenden. Aber ich habe das Salz der Erklärung von Dave genommen. Ich habe den Code in Python umgeschrieben, da ich selbst daran arbeite und ihn als guten Ersatz für mathematische Pakete betrachte.

Wenn Sie das Thema des Bayes-Theorems besser verstehen möchten, sind Sie herzlich willkommen.

Formulierung des Problems

, “ ”. .

-, . , . , . . , . . - .

, , , .

- $x$ . $x = 3$ . . .

( ) $N = 100$ () .

$\sigma_y^2=4$ .
, .

f_{p o s t e r i o r} (x) = \frac{f_{p r i o r} (x) \cdot f_{и з м} (x)}{\int f_{p r i o r} (x) \cdot f_{m e s} (x) d x},

$\begin{equation} f_{posterior}(x) = \frac{f_{prior}(x) \cdot f_{}(x)}{\int f_{prior}(x) \cdot f_{mes}(x) dx}, \end{equation}$

$f_{posterior}(x)$ — ;
$f_{prior}(x)$ — ;
$f_{mes}(x)$ — ( $L_x(sample)$ ).
. , ( , ):

f_{m e s} (x) = p d f (x = y, μ = x, σ = σ) = \frac{1}{2 π σ} e^{- \frac{(y - x)^{2}}{2 σ^{2}}},

$\begin{equation} f_{mes}(x) =pdf(x=y, \mu=x, \sigma=\sigma) = \frac{1}{2 \pi \sigma} e^{- \frac{(y-x)^2}{2\sigma^2}}, \end{equation}$

$pdf$ — ;
$\mu$ — ;
$\sigma$ — ;
$y$ — .
( $N$ ), , .

.
$\sigma$ , 99,7 %.

- , .

. -.
$(3, 5)$ . ( ) .

() , . .

:

f_{p o s t e r i o r} (X) = \frac{f_{p r i o r} (X) \cdot f_{и з м} (X)}{\int f_{p r i o r} (X) \cdot f_{m e s} (X) d X},

$\begin{equation} f_{posterior}(X) = \frac{f_{prior}(X) \cdot f_{}(X)}{\int f_{prior}(X) \cdot f_{mes}(X) dX}, \end{equation}$

$X$ — $\begin{pmatrix} x\\ y\end{pmatrix}$ ;
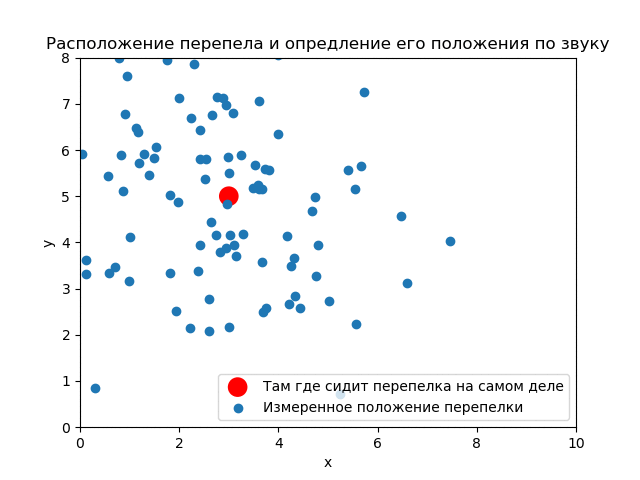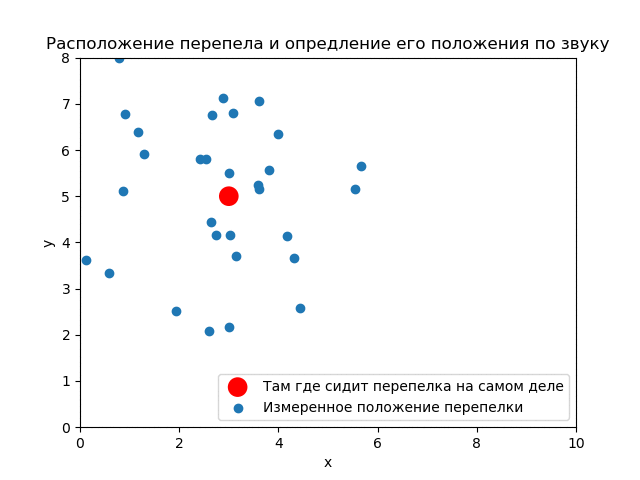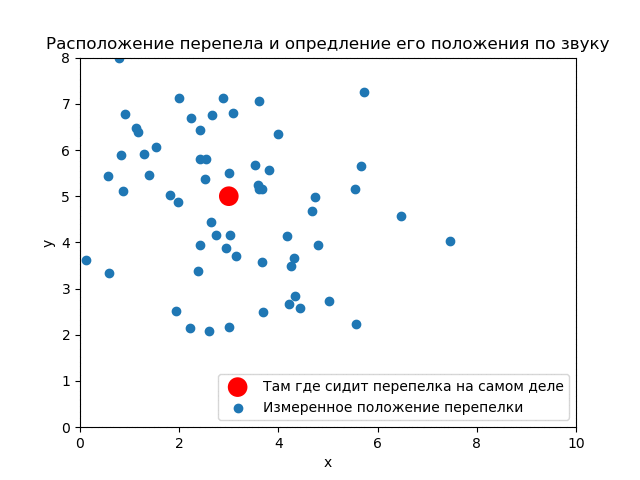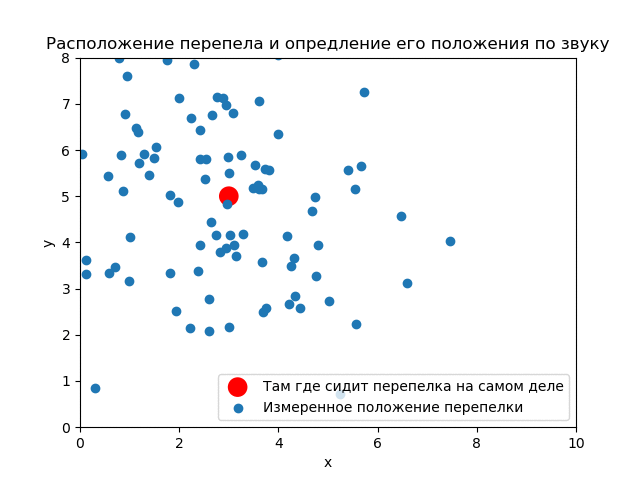
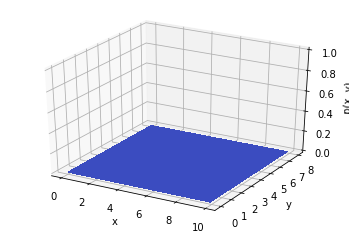
$f_{posterior}(X)$ — ;
$f_{prior}(X)$ — ;
$f_{mes}(X)$ — .
:

f_{m e s} (X) = \frac{1}{(2 π)^{2} d e t K} e^{\frac{1}{2} (Y - X)^{T} K^{- 1} (Y - X)},

$\begin{equation} f_{mes}(X) = \frac{1}{(2\pi)^2 detK} e^{ \frac {1}{2} (Y-X)^T K^{-1} (Y-X)}, \end{equation}$

$K$ — ;
$Y$ — $\begin{pmatrix} x\\ y\end{pmatrix}$ .
, .

.

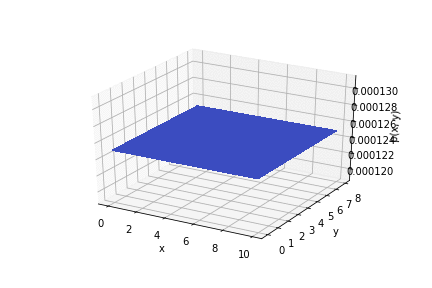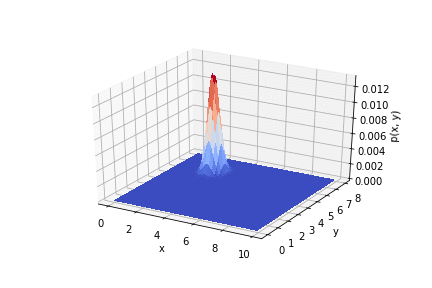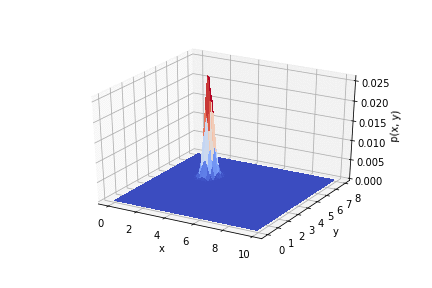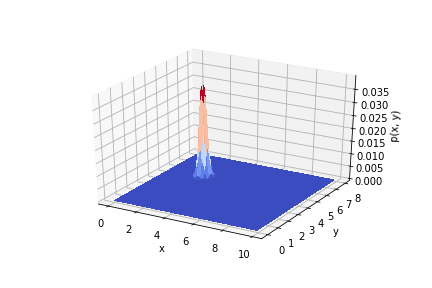
Somit ist ersichtlich, wie die Ergebnisse des Experiments die a priori-Verteilung beeinflussen. Wenn Sie die Messungen korrekt verwenden, können Sie eine gute Genauigkeit erzielen.
Aber ist es nicht einfacher, nur den Durchschnitt aller Messungen zu ermitteln und so den Standort der Wachtel zu beurteilen? Na sicher. Dieses Beispiel ist nur ein gutes Beispiel für den Bayes-Satz für kontinuierliche Zufallsvariablen. Der Zweck des Artikels ist es, die Theorie zu regeln.

Besuchen Sie den Dave Channel in diesen Wochen der Selbstisolation. Gut zu allen.

Bayesian Ninja

Formulierung des Problems

More articles: