Schönen Tag.
In meiner Freizeit habe ich ein wenig recherchiert.
In der Graphentheorie ist ein Algorithmus für gierige Klickzahlen bekannt. Weit davon entfernt, immer das richtige Ergebnis zu erzielen. Unter dem Schnitt wird eine Analyse der Ergebnisse des Greedy-Algorithmus durchgeführt, wenn diese mit einer teilweisen Aufzählung der Scheitelpunktsätze in den Diagrammen aus dem DIMACS-Benchmark-Satz kombiniert wird.
Die Spalte "Am bekanntesten" in Tabelle 1 zeigt die Größe der derzeit bekannten maximalen Klicks der angezeigten Diagramme. In der Spalte "Greedy" werden die maximalen Klickgrößen angezeigt, die vom Greedy-Algorithmus ermittelt wurden. Der gierige Algorithmus gibt nur in 3 von 35 Fällen die richtige Antwort.
Hinweis - Im implementierten Programmcode wählt der Greedy-Algorithmus den Scheitelpunkt mit dem höchsten Adjazenzwert aus. Wenn mehrere ähnliche Scheitelpunkte gefunden werden, wird der erste gefundene ausgewählt. Wir werden die Greedy-Algorithmus-Prozedur Greedy (A) nennen, wobei A die Nummer des Arrays (Adjazenzmatrix) ist, auf das der Algorithmus angewendet wird. Indizieren Sie das ursprüngliche Array als A0.
Tabelle 1 - Die Ergebnisse des in Pascal implementierten Algorithmus.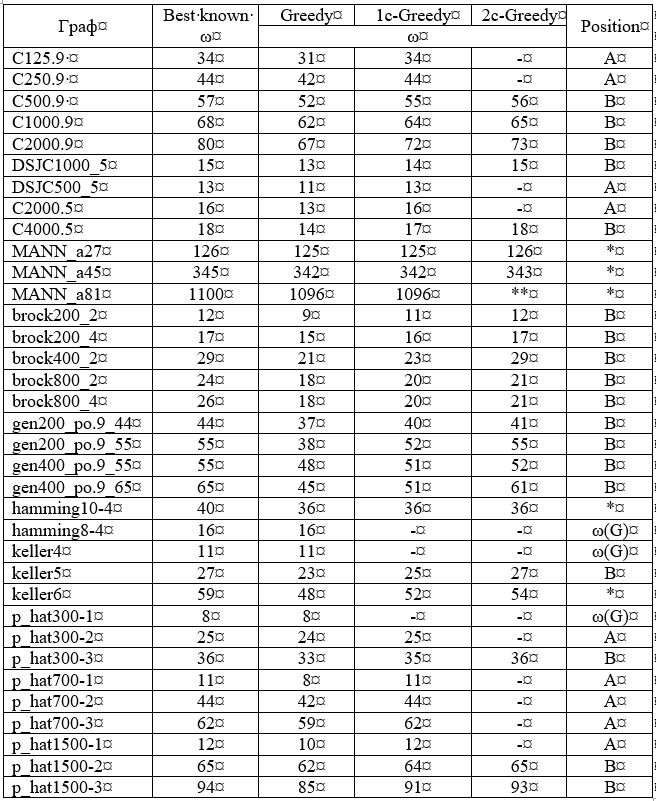 ** - aufgrund der Größe des Diagramms nicht analysiert.
** - aufgrund der Größe des Diagramms nicht analysiert., : N , . m, m – . DelNotAdj(m).
Greedy(m). ( ) «1c-Greedy». , , 8 35.
. , DelNotAdj(m). 0, m. mx. Greedy(mx). ( ) «2-Greedy».
3- (3c-Greedy) C500.9 C1000.9 ω(C500.9)=57, ω(C1000.9)=66.
.
Pascal Greedy(A) O(n2), n – . n , 2- – .. , ω(G) – () . .
, , ? 1 , .
( 1). O(n), – ω 1 ω(G) – , ωGR – , .
 1
1«Position» 1 . ꞷ(G) , . «» , .
«B» , 2- .
«*» , «», .. 2, 3 . ω. ωGRCFG.
, , , , . .. , , , 2- .
«» , :
- 0 «» . ωGR.
- «» m, m . m , . ωGR+1.
- «» mn, m- n- 0. mn , n- m- . ωGR+2.
- 3-, 4-,…, y- ωGR+3, ωGR+4,…, ωGR+y .
- 0 — ω(G).
. «» «B» :
, , ωGR. ωGR+1 ωGR, 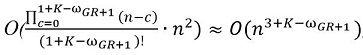 , K – .
, K – .
«*» :
«» ωGR, ωGR+1, ωGR+2,…, ω(G) . , , . , ωGR.
: ωGR, ωGR+1, ωGR+2,… , « » ( ωGRCDE 1).
:
1. «» ωGR+y,
ωGR+y-1, 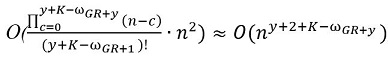 , K – .
, K – .
.
2. y- ωGR+y, , .. ωGR+y=ωGR+y-1, , ωGR+y ω(G) .
Wenn das oben Gesagte die Arbeit eines anderen wiederholt, bin ich nicht aus Trotz, ich werde mich freuen, den Link zu sehen. Umso mehr würde ich mich freuen, wenn jemand theoretisch die vorgeschlagenen Hypothesen beweisen oder widerlegen kann.