👌🏿 ♉️ 💃🏿 Vergleich der Dynamik von Notierungen zweier Aktien in Python am Beispiel von Vorzugs- und Stammaktien der Sberbank 👨‍🎤 🔉 🥀

Hallo, heute möchte ich über meine Erfahrungen bei der Analyse von Sberbank-Aktien sprechen. Manchmal zeigen sie eine etwas andere Dynamik - es wurde für mich interessant, die Bewegung ihrer Zitate zu analysieren.

In diesem Beispiel werden Angebote von der Finam-Website heruntergeladen. Link zum Herunterladen der regulären Sberbank .

Für Spaltenoperationen verwende ich Pandas, für die Matplotlib-Visualisierung.

Wir importieren:

import pandas as pd
import matplotlib.pyplot as plt

Um zu verhindern, dass Tabellen verkleinert werden, müssen Sie die folgenden Einschränkungen aufheben:

pd.set_option('display.max_columns', None)
pd.set_option('display.expand_frame_repr', False)
pd.set_option('max_colwidth', 80)
pd.set_option('max_rows', 6000)

Bestandsdaten lesen

df = pd.read_csv("SBER_190101_200105.csv",sep=';', header=0, index_col='<DATE>', parse_dates=True)

(Geben Sie das Trennzeichen an, in dem sich die Spaltennamen befinden. Welche Spalte der Index sein soll, aktivieren Sie die Datumsanalyse.)

Geben Sie auch die Sortierung an:

df = df.sort_values(by='<DATE>')

Wir zeigen unsere Daten an:

print(df)

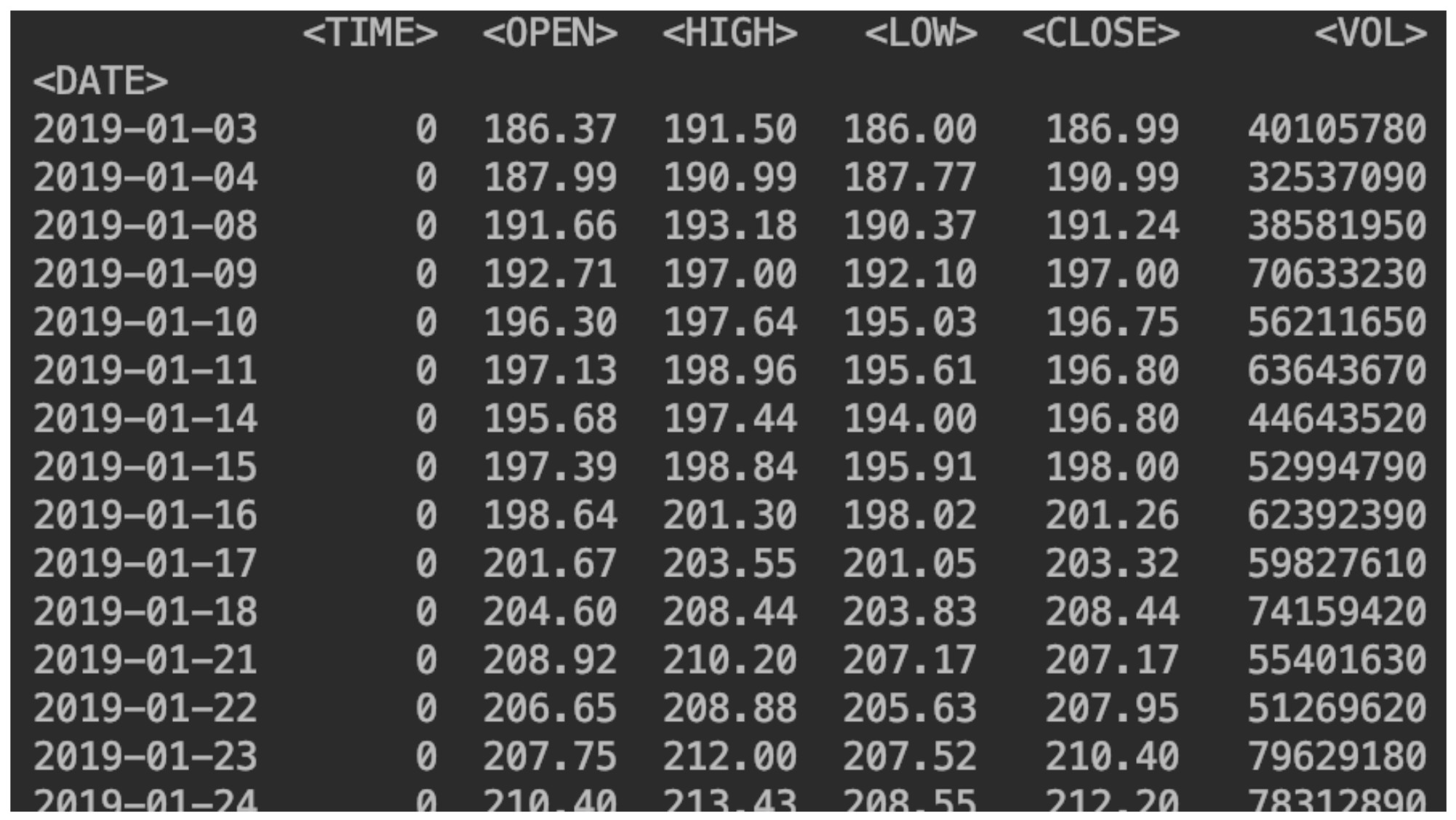Fügen Sie eine Spalte mit einer Preisänderung hinzu

df['returns']=(df['<CLOSE>']/df['<CLOSE>'].shift(1))-1

So ist es möglich, genau den Prozentsatz abzuleiten:

df['returns_pers']=((df['<CLOSE>']/df['<CLOSE>'].shift(1))-1)*100

Fügen Sie eine zweite Freigabe hinzu

Mach es genauso.

df2 = pd.read_csv("SBERP_190101_200105.csv",sep=';', header=0, index_col='<DATE>', parse_dates=True)

df = df.sort_values(by='<DATE>')

df2['returns_pers']=((df2['<CLOSE>']/df2['<CLOSE>'].shift(1))-1)*100
df2['returns']=(df2['<CLOSE>']/df2['<CLOSE>'].shift(1))-1
print(df2)

Wir visualisieren unsere Börsenkurse

df['<CLOSE>'].plot(label='sber')
df2['<CLOSE>'].plot(label='sberp')
plt.legend()
plt.show()

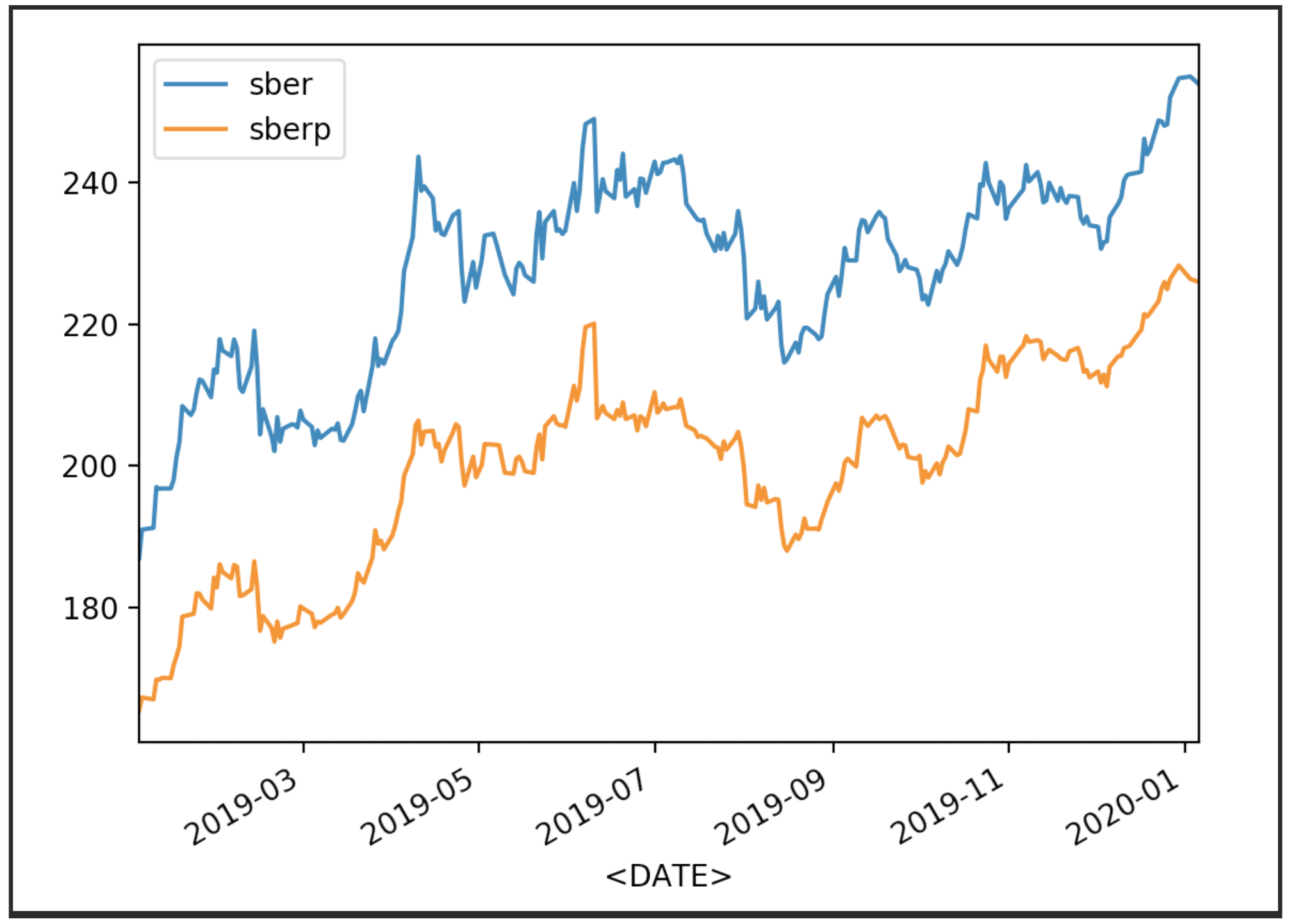Zeigen Sie nun die Anführungszeichen mit ihrem Durchschnitt an (MA 50):

df['<CLOSE>'].plot(label='sber')
df2['<CLOSE>'].plot(label='sberp')
df['ma50'] = df['<OPEN>'].rolling(50).mean().plot(label='ma50')
df2['ma50'] = df2['<OPEN>'].rolling(50).mean().plot(label='ma50')
plt.legend()
plt.show()

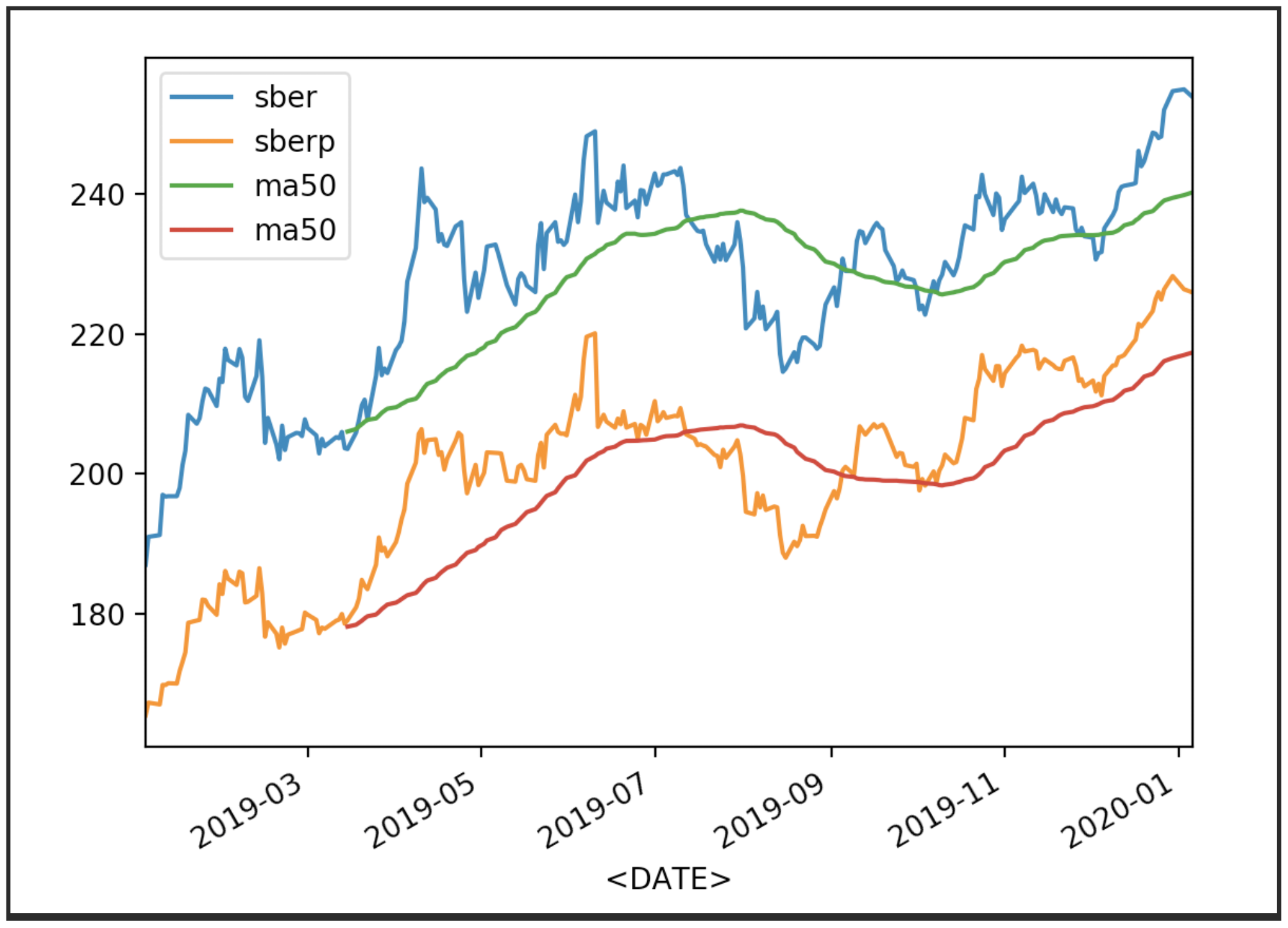Es können auch andere Durchschnittswerte angezeigt werden.

df['<CLOSE>'].plot(label='sber')
df2['<CLOSE>'].plot(label='sberp')
df['ma100'] = df['<OPEN>'].rolling(100).mean().plot(label='ma100')
df2['ma100'] = df2['<OPEN>'].rolling(100).mean().plot(label='ma100')
plt.legend()
plt.show()

Jetzt zeigen wir den Umsatz für die Aktien an:
Fügen Sie auch den Namen der Y-Achse
und die Größe der Leinwand hinzu

df['total_trade'] = df['<OPEN>']*df['<VOL>']
df2['total_trade'] = df2['<OPEN>']*df2['<VOL>']
df['total_trade'].plot(label='sber',figsize=(16,8))
df2['total_trade'].plot(label='sberp',figsize=(16,8))
plt.legend()
plt.ylabel('Total Traded')
plt.show()

Korrelationsanalyse

Schauen wir uns nun die Korrelation genauer an. Ein Matrixdiagramm hilft uns dabei.

Erstellen Sie eine neue Tabelle mit Spalten für beide Bestände und geben Sie ihnen Namen.

all_sber = pd.concat([df['<OPEN>'],df2['<OPEN>']],axis=1)
all_sber.columns = ['sber_open','sberp_open']
print(all_sber)

Jetzt importieren wir den notwendigen Zeitplan

from pandas.plotting import scatter_matrix

Und geben Sie es aus:

scatter_matrix(all_sber,figsize=(8,8),alpha=0.2,hist_kwds={'bins':100});
plt.show()

Es sollte klargestellt werden, dass wir Transparenz hinzufügen müssen (Alpha = 0,2), um die Überlappung von Punkten zu sehen.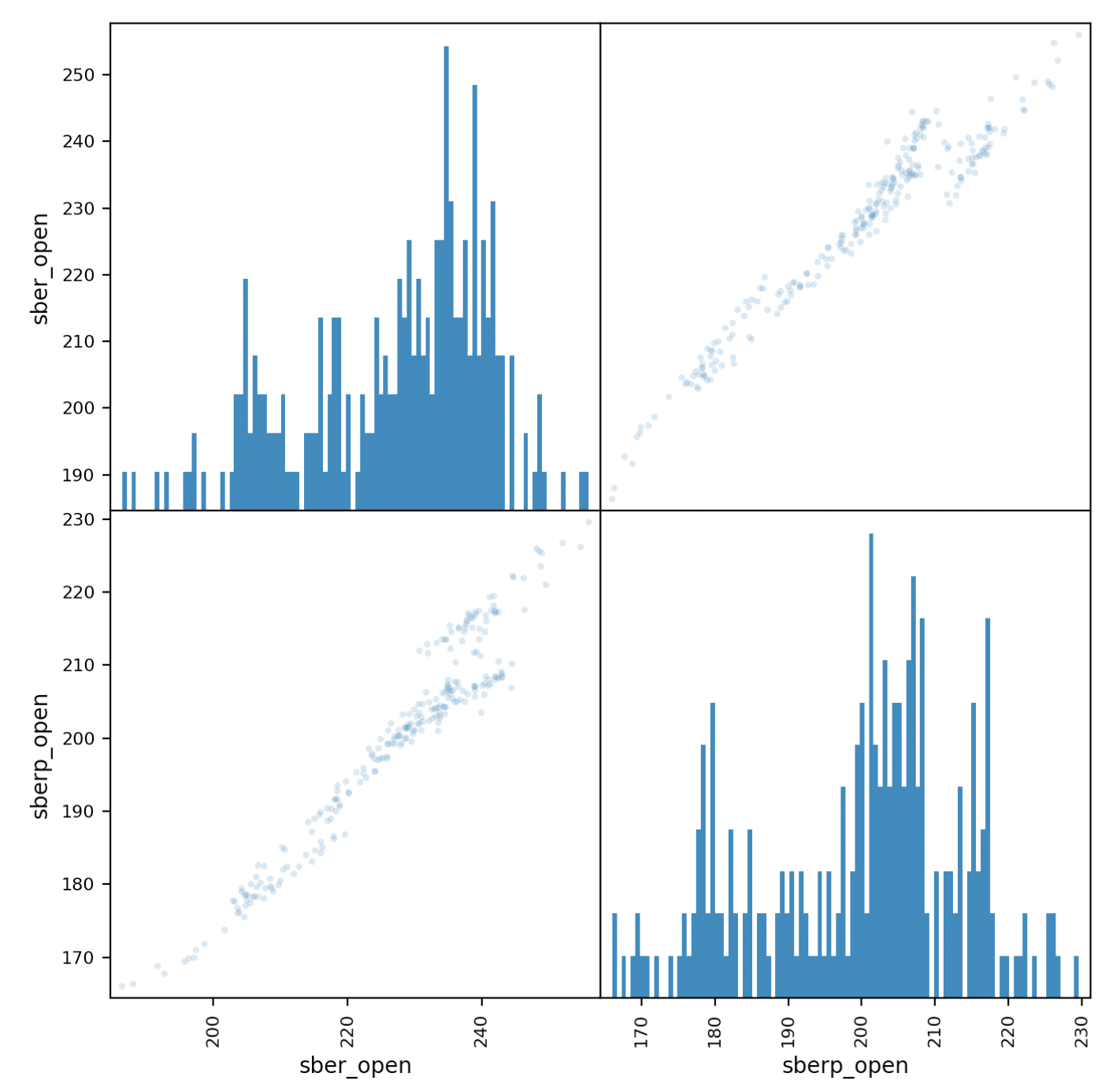

Wenn die Punkte entlang der Diagonale „gehen“, wird eine Korrelation beobachtet.

Bewertung der Wertpapiervolatilität

df['returns_pers'].plot(label='sber')
df2['returns_pers'].plot(label='sberp')
plt.legend()
plt.show()

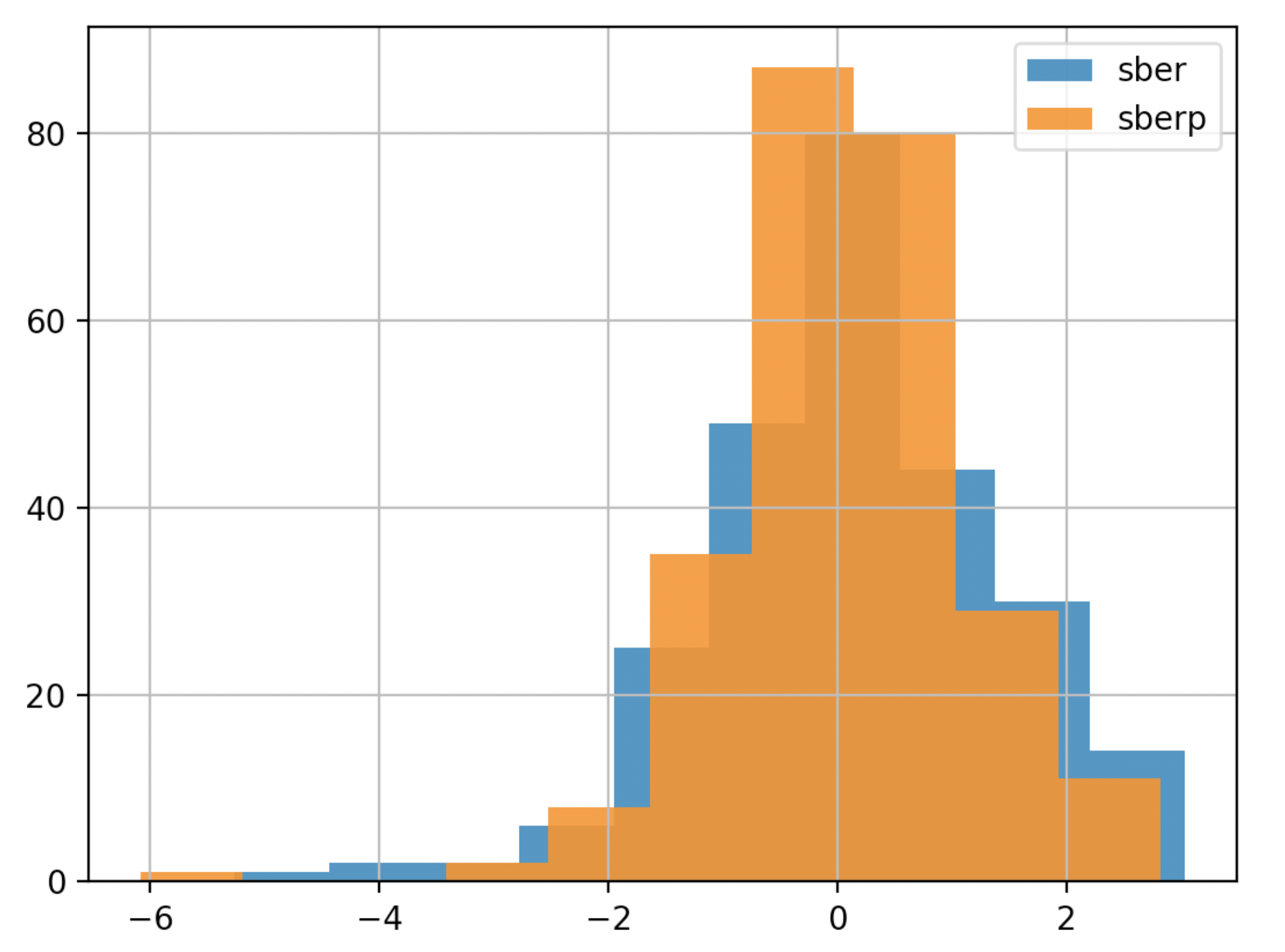
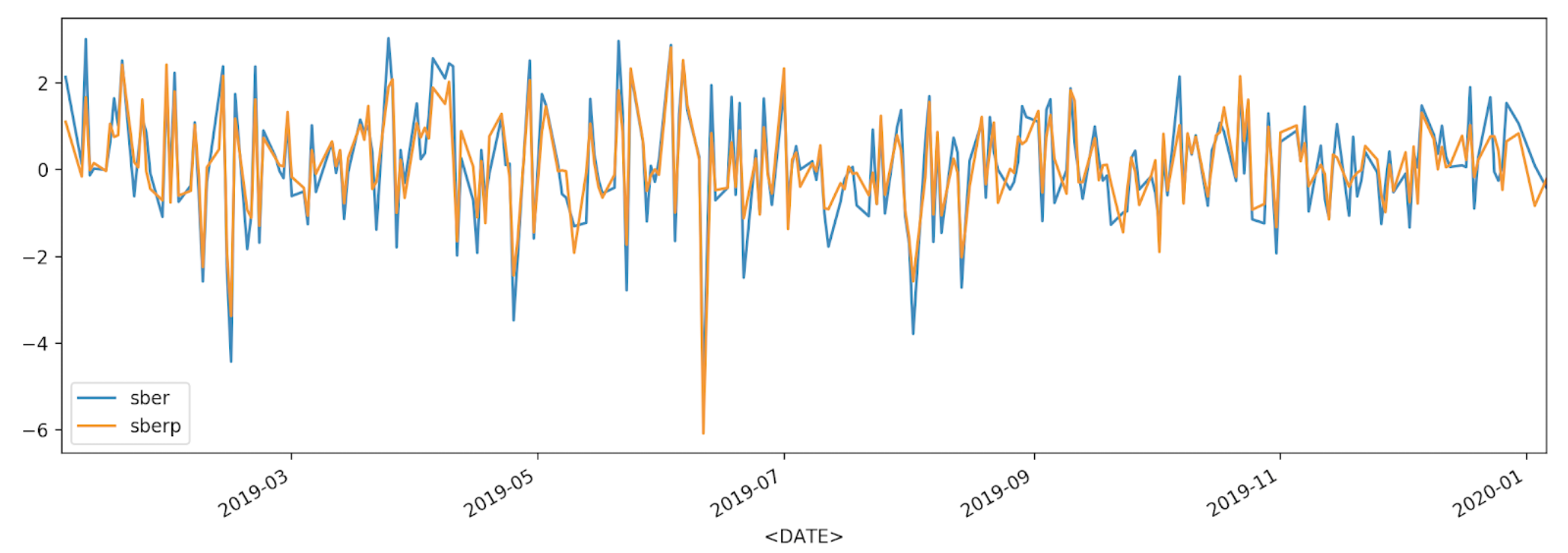Zum besseren Verständnis werden wir die Volatilität in einem anderen Diagramm anzeigen - einem Histogramm

df['returns_pers'].hist(bins=100,label='sber',alpha=0.5)
df2['returns_pers'].hist(bins=100,label='sberp',alpha=0.5)
plt.legend()
plt.show()

Um eine Schlussfolgerung schneller zu ziehen, können Sie den Zeitplan vereinfachen (wir werden das Diagramm weniger detailliert und weniger transparent machen):

df['returns_pers'].hist(bins=10,label='sber',alpha=0.9)
df2['returns_pers'].hist(bins=10,label='sberp',alpha=0.9)
plt.legend()
plt.show()

Kumulierte Umsatzanalyse

Nun leiten wir die prozentuale Wertänderung der Aktien ab.

Geben Sie dazu die Spalte mit dem kumulierten Einkommen ein.

df['Cumulative Return'] = (1+ df['returns']).cumprod()
df2['Cumulative Return'] = (1+ df2['returns']).cumprod()
print(df)
print(df2)

df['Cumulative Return'].plot(label='sber')
df2['Cumulative Return'].plot(label='sberp')
plt.legend()
plt.show()

In den Diagrammen sehen wir die Zeitintervalle, in denen eine der Aktien im Verhältnis zur anderen unterschätzt oder neu bewertet wird. Unter den gegenwärtigen Umständen (ceteris paribus, bitte beachten Sie) hilft uns dies bei der Auswahl einer Aktie, die im Durchschnitt liegt, wenn die Kapitalisierung der Sberbank sinkt.