Hallo Habr!Wir erinnern Sie daran, dass wir früher das Buch " Maschinelles Lernen ohne zusätzliche Wörter " angekündigt haben - und jetzt ist es bereits im Verkauf . Trotz der Tatsache, dass das Buch für Anfänger in MO tatsächlich zu einem Desktop werden kann , wurden einige Themen darin immer noch nicht berührt. Daher bieten wir allen Interessierten eine Übersetzung eines Artikels von Simon Kerstens über die Essenz von MCMC- Algorithmen mit der Implementierung eines solchen Algorithmus in Python an.Monte-Carlo-Methoden für Markov-Ketten (MCMC) sind eine leistungsstarke Klasse von Methoden zur Abtastung aus Wahrscheinlichkeitsverteilungen, die nur bis zu einer bestimmten (unbekannten) Normalisierungskonstante bekannt sind.Bevor wir uns jedoch mit dem MCMC befassen, wollen wir diskutieren, warum Sie möglicherweise überhaupt eine solche Auswahl treffen müssen. Die Antwort lautet: Möglicherweise interessieren Sie sich entweder für die Stichproben selbst aus der Stichprobe (z. B. um unbekannte Parameter mithilfe der Bayes'schen Ableitungsmethode zu bestimmen) oder um die erwarteten Werte der Funktionen in Bezug auf die Wahrscheinlichkeitsverteilung zu approximieren (z. B. um thermodynamische Größen aus der Zustandsverteilung in der statistischen Physik zu berechnen). Manchmal interessiert uns nur der Wahrscheinlichkeitsverteilungsmodus. In diesem Fall erhalten wir es durch die Methode der numerischen Optimierung, so dass es nicht erforderlich ist, eine vollständige Auswahl zu treffen.Es stellt sich heraus, dass das Abtasten aus Wahrscheinlichkeitsverteilungen mit Ausnahme der primitivsten eine schwierige Aufgabe ist. Die inverse Transformationsmethode ist eine elementare Technik zum Abtasten aus Wahrscheinlichkeitsverteilungen, die jedoch die Verwendung einer kumulativen Verteilungsfunktion erfordert. Um diese wiederum verwenden zu können, müssen Sie die Normalisierungskonstante kennen, die normalerweise unbekannt ist. Im Prinzip kann eine Normalisierungskonstante durch numerische Integration erhalten werden, aber dieses Verfahren wird mit zunehmender Anzahl von Dimensionen schnell nicht praktikabel. AbweichungsabtastungEs erfordert keine normalisierte Verteilung, aber um sie effektiv umzusetzen, ist es sehr wichtig, über die Verteilung des Interesses an uns Bescheid zu wissen. Darüber hinaus leidet diese Methode stark unter dem Fluch der Dimensionen - dies bedeutet, dass ihre Wirksamkeit mit zunehmender Anzahl von Variablen schnell abnimmt. Aus diesem Grund müssen Sie den Empfang repräsentativer Proben aus Ihrer Verteilung intelligent organisieren, ohne die Normalisierungskonstante kennen zu müssen.MCMC-Algorithmen sind eine Klasse von Methoden, die speziell dafür entwickelt wurden. Sie gehen zurück auf den wegweisenden Artikel von Metropolis und anderen ; Metropolis entwickelte den ersten nach ihm benannten MCMC-Algorithmusund entworfen, um den Gleichgewichtszustand eines zweidimensionalen Systems harter Kugeln zu berechnen. Tatsächlich suchten die Forscher nach einer universellen Methode, mit der wir die in der statistischen Physik gefundenen erwarteten Werte berechnen können.Dieser Artikel behandelt die Grundlagen der MCMC-Probenahme.MARKOV-KETTENNachdem wir verstanden haben, warum wir Proben nehmen müssen, gehen wir zum Herzen von MCMC über: Markov-Ketten. Was ist eine Markov-Kette? Ohne auf technische Details einzugehen, können wir sagen, dass eine Markov-Kette eine zufällige Folge von Zuständen in einem bestimmten Zustandsraum ist, wobei die Wahrscheinlichkeit, einen bestimmten Zustand zu wählen, nur vom aktuellen Zustand der Kette abhängt, nicht jedoch von ihrer Vergangenheit: Diese Kette ist ohne Gedächtnis. Unter bestimmten Bedingungen hat eine Markov-Kette eine einzigartige stationäre Verteilung von Zuständen, zu denen sie konvergiert und eine bestimmte Anzahl von Zuständen überwindet. Nach einer solchen Anzahl von Zustandszuständen in einer Markov-Kette wird eine invariante Verteilung erhalten.Um aus einer Verteilung 
abzutasten, erstellt und simuliert der MCMC-Algorithmus eine Markov-Kette, deren stationäre Verteilung ist;; Dies bedeutet, dass nach der anfänglichen "Keim" -Periode die Zustände einer solchen Markov-Kette nach dem Prinzip verteilt werden . Daher müssen wir nur den Status speichern, um Proben von zu erhalten .Betrachten wir zu Bildungszwecken sowohl einen diskreten Zustandsraum als auch eine diskrete „Zeit“. Die Schlüsselgröße, die eine Markov-Kette kennzeichnet, ist ein Übergangsoperator 
, der die Wahrscheinlichkeit angibt, 
zu einem bestimmten Zeitpunkt in einem Zustand zu sein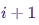 
, vorausgesetzt, die Kette befindet sich zu einem bestimmten 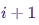Zeitpunkt in einem Zustand i.Lassen Sie uns jetzt nur zum Spaß (und als Demonstration) schnell eine Markov-Kette mit einer einzigartigen stationären Verteilung weben. Beginnen wir mit einigen Importen und Einstellungen für Diagramme:%matplotlib notebook
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10, 6]
np.random.seed(42)
Die Markov-Kette umrundet den diskreten Zustandsraum, der durch drei Wetterbedingungen gebildet wird:state_space = ("sunny", "cloudy", "rainy")
In einem diskreten Zustandsraum ist der Übergangsoperator nur eine Matrix. In unserem Fall entsprechen die Spalten und Zeilen sonnigem, bewölktem und regnerischem Wetter. Wählen wir relativ vernünftige Werte für die Wahrscheinlichkeiten aller Übergänge:transition_matrix = np.array(((0.6, 0.3, 0.1),
(0.3, 0.4, 0.3),
(0.2, 0.3, 0.5)))
Die Zeilen geben die Zustände an, in denen sich die Schaltung derzeit befinden kann, und die Spalten geben die Zustände an, in die die Schaltung gehen kann. Wenn wir den Zeitschritt der Markov-Kette in einer Stunde machen, besteht eine 60% ige Chance, dass das sonnige Wetter für die nächste Stunde anhält, vorausgesetzt, es ist jetzt sonnig. Es besteht auch eine Wahrscheinlichkeit von 30%, dass es in der nächsten Stunde bewölkt wird, und eine Wahrscheinlichkeit von 10%, dass es unmittelbar nach sonnigem Wetter regnet. Dies bedeutet auch, dass sich die Werte in jeder Zeile zu eins addieren.Lassen Sie uns unsere Markov-Kette ein wenig fahren:n_steps = 20000
states = [0]
for i in range(n_steps):
states.append(np.random.choice((0, 1, 2), p=transition_matrix[states[-1]]))
states = np.array(states)
Wir können beobachten, wie die Markov-Kette zu einer stationären Verteilung konvergiert, indem wir die empirische Wahrscheinlichkeit jedes Zustands als Funktion der Kettenlänge berechnen:def despine(ax, spines=('top', 'left', 'right')):
for spine in spines:
ax.spines[spine].set_visible(False)
fig, ax = plt.subplots()
width = 1000
offsets = range(1, n_steps, 5)
for i, label in enumerate(state_space):
ax.plot(offsets, [np.sum(states[:offset] == i) / offset
for offset in offsets], label=label)
ax.set_xlabel("number of steps")
ax.set_ylabel("likelihood")
ax.legend(frameon=False)
despine(ax, ('top', 'right'))
plt.show()
EHREN ALLER MCMC: METROPOLIS-HASTINGS-ALGORITHMUSNatürlich ist dies alles sehr interessant, aber zurück zum Stichprobenprozess einer beliebigen Wahrscheinlichkeitsverteilung 
. Es kann entweder diskret sein, in welchem Fall wir weiter über die Übergangsmatrix sprechen 
, oder kontinuierlich, in welchem Fall es ein Übergangskern sein wird. Im Folgenden werden wir über kontinuierliche Verteilungen sprechen, aber alle Konzepte, die wir hier betrachten, sind auch auf diskrete Fälle anwendbar.Wenn wir den Übergangskern so gestalten könnten, dass der nächste Zustand bereits abgeleitet wurde , dann könnte dies begrenzt sein, da unsere Markov-Kette ... direkt von abtasten würde . Um dies zu erreichen, benötigen wir leider die Möglichkeit, Proben zu entnehmenwas wir nicht können - sonst würdest du das nicht lesen, oder?Die Problemumgehung besteht darin, den Übergangskern 
in zwei Teile zu unterteilen: den Vorschlagsschritt und den Akzeptanz- / Ablehnungsschritt. Eine Hilfsverteilung erscheint im Probenschritt
aus denen die möglichen nächsten Zustände der Kette ausgewählt werden. Wir können nicht nur eine Auswahl aus dieser Verteilung treffen, sondern auch die Verteilung selbst willkürlich auswählen. Beim Entwerfen sollte man sich jedoch bemühen, zu einer Konfiguration zu gelangen, bei der aus dieser Verteilung entnommene Proben nur minimal mit dem aktuellen Zustand korrelieren und gleichzeitig gute Chancen haben, die Empfangsphase zu durchlaufen. Der obige Empfangs- / Verwerfungsschritt ist der zweite Teil des Übergangskerns; Zu diesem Zeitpunkt werden Fehler in den ausgewählten Testzuständen korrigiert 
. Hier wird die Wahrscheinlichkeit eines erfolgreichen Empfangs berechnet 
und eine Stichprobe mit einer solchen Wahrscheinlichkeit wie dem nächsten Zustand in der Kette entnommen . Den nächsten Zustand erhalten vondann wie folgt durchgeführt: Zuerst wird der Versuchszustand entnommen . Dann wird es als nächster Zustand mit Wahrscheinlichkeit genommen oder mit Wahrscheinlichkeit verworfen 
, und im letzteren Fall wird der aktuelle Zustand kopiert und als nächster verwendet.Folglich haben wir
ausreichende Bedingungen für die Markov-Kette, da eine stationäre Verteilung wie folgt ist: Der Übergangskern muss ein detailliertes Gleichgewicht aufweisen oder wie in der physikalischen Literatur geschrieben, mikroskopische Reversibilität :
.Dies bedeutet, dass die Wahrscheinlichkeit, in einem Zustand zu sein 
und von dort nach zu ziehen
muss gleich der Wahrscheinlichkeit des umgekehrten Prozesses sein, dh in der Lage sein und in einen Zustand gehen . Die Übergangskerne der meisten MCMC-Algorithmen erfüllen diese Bedingung.Damit der zweiteilige Übergangskern dem detaillierten Gleichgewicht entspricht, muss er richtig auswählen, dh 
sicherstellen, dass Sie Asymmetrien im Wahrscheinlichkeitsstrom von / nach oder korrigieren können . Der Metropolis-Hastings-Algorithmus verwendet das Zulässigkeitskriterium Metropolis :
.Und hier beginnt die Magie: Wir kennen nur eine Konstante, aber es spielt keine Rolle, da diese unbekannte Konstante den Ausdruck für aufhebt! Es ist diese paccpacc-Eigenschaft, die den Betrieb von Algorithmen sicherstellt, die auf dem Metropolis-Hastings-Algorithmus für nicht normalisierte Verteilungen basieren. Oft werden symmetrische Hilfsverteilungen c verwendet 
. In diesem Fall wird der Metropolis-Hastings-Algorithmus auf den ursprünglichen (weniger allgemeinen) Metropolis-Algorithmus reduziert, der 1953 entwickelt wurde. Im ursprünglichen Algorithmus
.In diesem Fall kann der gesamte Übergangskern der Metropolis-Hastings als geschrieben werden
.WIR UMSETZEN DEN METROPOLIS-HASTINGS-ALGORITHMUS BEI PYTHONNun, da wir herausgefunden haben, wie der Metropolis-Hastings-Algorithmus funktioniert, fahren wir mit seiner Implementierung fort. Zunächst legen wir die logarithmische Wahrscheinlichkeit der Verteilung fest, aus der wir eine Auswahl treffen werden - ohne Normalisierungskonstanten; es wird angenommen, dass wir sie nicht kennen. Als nächstes arbeiten wir mit der Standardnormalverteilung:def log_prob(x):
return -0.5 * np.sum(x ** 2)
Als nächstes wählen wir eine symmetrische Hilfsverteilung. Im Allgemeinen kann die Leistung des Metropolis-Hastings-Algorithmus verbessert werden, wenn Sie bereits bekannte Informationen über die Verteilung, aus der Sie eine Auswahl treffen möchten, in die Hilfsverteilung aufnehmen. Ein vereinfachter Ansatz sieht folgendermaßen aus: Wir nehmen den aktuellen Status xund wählen eine Stichprobe aus , dh stellen eine bestimmte Schrittgröße ein Δund gehen von unserem aktuellen Status um nicht mehr als 
:def proposal(x, stepsize):
return np.random.uniform(low=x - 0.5 * stepsize,
high=x + 0.5 * stepsize,
size=x.shape)
Schließlich berechnen wir die Wahrscheinlichkeit, dass der Vorschlag angenommen wird:def p_acc_MH(x_new, x_old, log_prob):
return min(1, np.exp(log_prob(x_new) - log_prob(x_old)))
Jetzt fassen wir all dies zu einer wirklich kurzen Implementierung der Abtaststufe für den Metropolis-Hastings-Algorithmus zusammen:def sample_MH(x_old, log_prob, stepsize):
x_new = proposal(x_old, stepsize)
accept = np.random.random() < p_acc(x_new, x_old, log_prob)
if accept:
return accept, x_new
else:
return accept, x_old
Zusätzlich zum nächsten Status in der Markov-Kette x_newoder geben x_oldwir auch Informationen darüber zurück, ob der MCMC-Schritt übernommen wurde. Auf diese Weise können wir die Dynamik der Probensammlung verfolgen. Zum Abschluss dieser Implementierung schreiben wir eine Funktion, die iterativ sample_MHeine Markov-Kette aufruft und somit aufbaut:def build_MH_chain(init, stepsize, n_total, log_prob):
n_accepted = 0
chain = [init]
for _ in range(n_total):
accept, state = sample_MH(chain[-1], log_prob, stepsize)
chain.append(state)
n_accepted += accept
acceptance_rate = n_accepted / float(n_total)
return chain, acceptance_rate
UNSEREN METROPOLIS-HASTINGS-ALGORITHMUS PRÜFEN UND SEIN VERHALTEN FORSCHENWahrscheinlich können Sie es jetzt nicht erwarten, all dies in Aktion zu sehen. Wir werden dies tun, wir werden einige fundierte Entscheidungen über die Argumente treffen stepsizeund n_total:chain, acceptance_rate = build_MH_chain(np.array([2.0]), 3.0, 10000, log_prob)
chain = [state for state, in chain]
print("Acceptance rate: {:.3f}".format(acceptance_rate))
last_states = ", ".join("{:.5f}".format(state)
for state in chain[-10:])
print("Last ten states of chain: " + last_states)
Acceptance rate: 0.722
Last ten states of chain: -0.84962, -0.84962, -0.84962, -0.08692, 0.92728, -0.46215, 0.08655, -0.33841, -0.33841, -0.33841
Alles ist gut. Also, hat es funktioniert? In etwa 71% der Fälle ist es uns gelungen, Proben zu entnehmen, und wir haben eine Kette von Staaten. Die ersten Zustände, in denen die Kette noch nicht zu ihrer stationären Verteilung konvergiert hat, sollten verworfen werden. Lassen Sie uns überprüfen, ob die von uns gewählten Bedingungen tatsächlich eine Normalverteilung haben:def plot_samples(chain, log_prob, ax, orientation='vertical', normalize=True,
xlims=(-5, 5), legend=True):
from scipy.integrate import quad
ax.hist(chain, bins=50, density=True, label="MCMC samples",
orientation=orientation)
if normalize:
Z, _ = quad(lambda x: np.exp(log_prob(x)), -np.inf, np.inf)
else:
Z = 1.0
xses = np.linspace(xlims[0], xlims[1], 1000)
yses = [np.exp(log_prob(x)) / Z for x in xses]
if orientation == 'horizontal':
(yses, xses) = (xses, yses)
ax.plot(xses, yses, label="true distribution")
if legend:
ax.legend(frameon=False)
fig, ax = plt.subplots()
plot_samples(chain[500:], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()
Das sieht großartig aus!Was ist mit den Parametern stepsizeund n_total? Wir diskutieren zuerst die Schrittgröße: Sie bestimmt, wie weit der Versuchszustand vom aktuellen Zustand der Schaltung entfernt werden kann. Daher ist dies ein Hilfsverteilungsparameter q, der steuert, wie groß die zufälligen Schritte der Markov-Kette sein werden. Wenn die Schrittgröße zu groß ist, landen die Versuchszustände häufig am Ende der Verteilung, wo die Wahrscheinlichkeitswerte niedrig sind. Der Metropolis-Hastings-Abtastmechanismus verwirft die meisten dieser Schritte, wodurch die Empfangsraten verringert werden und die Konvergenz erheblich verlangsamt wird. Überzeugen Sie sich selbst:def sample_and_display(init_state, stepsize, n_total, n_burnin, log_prob):
chain, acceptance_rate = build_MH_chain(init_state, stepsize, n_total, log_prob)
print("Acceptance rate: {:.3f}".format(acceptance_rate))
fig, ax = plt.subplots()
plot_samples([state for state, in chain[n_burnin:]], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()
sample_and_display(np.array([2.0]), 30, 10000, 500, log_prob)
Acceptance rate: 0.116
Nicht sehr cool, oder? Jetzt scheint es am besten zu sein, eine winzige Schrittgröße einzustellen. Es stellt sich heraus, dass dies auch keine kluge Entscheidung ist, da die Markov-Kette die Wahrscheinlichkeitsverteilung sehr langsam untersucht und daher auch nicht so schnell konvergiert wie bei einer gut gewählten Schrittgröße:sample_and_display(np.array([2.0]), 0.1, 10000, 500, log_prob)
Acceptance rate: 0.992
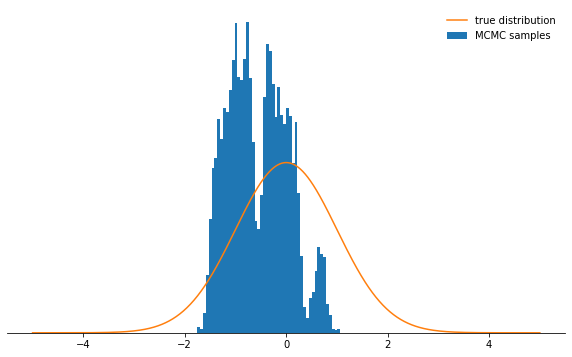Unabhängig davon, wie Sie den Schrittgrößenparameter auswählen, konvergiert die Markov-Kette schließlich zu einer stationären Verteilung. Dies kann jedoch viel Zeit in Anspruch nehmen. Die Zeit, in der wir die Markov-Kette simulieren, wird durch den Parameter bestimmt n_total- er bestimmt einfach, wie viele Zustände der Markov-Kette (und daher die ausgewählten Stichproben) wir letztendlich haben werden. Wenn die Kette langsam konvergiert, muss sie erhöht n_totalwerden, damit die Markov-Kette Zeit hat, den Ausgangszustand zu „vergessen“. Daher lassen wir die Schrittgröße winzig und erhöhen die Anzahl der Proben durch Erhöhen des Parameters n_total:sample_and_display(np.array([2.0]), 0.1, 500000, 25000, log_prob)
Acceptance rate: 0.990
Meeeedenly bewegen wir uns auf das Ziel zu ...SCHLUSSFOLGERUNGEN InAnbetracht all dieser Punkte hoffe ich, dass Sie jetzt die Essenz des Metropolis-Hastings-Algorithmus und seine Parameter intuitiv verstanden haben und verstehen, warum dies ein äußerst nützliches Werkzeug für die Auswahl von nicht standardmäßigen Wahrscheinlichkeitsverteilungen ist, auf die Sie in der Praxis stoßen können.Ich empfehle dringend, dass Sie mit dem hier angegebenen Code experimentieren .- Sie gewöhnen sich also an das Verhalten des Algorithmus unter verschiedenen Umständen und verstehen es besser. Versuchen Sie es mit einer asymmetrischen Hilfsverteilung! Was passiert, wenn Sie das Akzeptanzkriterium nicht richtig konfigurieren? Was passiert, wenn Sie versuchen, aus einer bimodalen Verteilung zu probieren? Können Sie eine Möglichkeit finden, die Schrittgröße automatisch anzupassen? Was sind die Fallstricke hier? Beantworten Sie diese Fragen selbst!