Nichtlineare Differentialgleichungen, Diskretion von Raum-Zeit und Epsilon-Produkt

Der gesamte Inhalt dieses Artikels ist eine Folge der Lösung des Problems des ersten Studienjahres des Instituts in mathematischer Analyse.

Hier stellen wir ein neues Produkt für Gitterfunktionen vor (wir werden es Epsilon-Multiplikation nennen), das uns die Möglichkeit gibt, einen interessanten Zusammenhang zwischen integralen Differentialgleichungen (einschließlich nichtlinearer) und Wiederholungsrelationen zu erkennen. Auf diese Weise können Sie einige Methoden zum Lösen aus einem ungewöhnlichen Blickwinkel betrachten.

Was mich jedoch besonders interessant fand, ist, dass die neue Arbeit es uns auch ermöglicht, über so grundlegende Dinge wie die Kontinuität der Raum-Zeit zu „spekulieren“. Diese Argumentation sollte natürlich eher als intellektuelle Übung betrachtet werden.

Es schien mir, dass dieser mathematische Rebus oder, wenn Sie möchten, eine kleine mathematische Reise auf dem Wissensstand des ersten oder zweiten Jahres einer technischen Universität Habr-Leser interessieren könnte, die sich für Mathematik interessieren.

Kommentar

• Sie werden keine Links sehen und im Allgemeinen ist dies alles das Ergebnis der Gedanken einer einzelnen Person
• Vielleicht (und sogar höchstwahrscheinlich) ist dies alles nicht neu, und vielleicht entsprechen einige der Begriffe, die ich verwende, nicht der mathematischen Tradition, aber da dies keine wissenschaftliche Veröffentlichung ist, gibt es keinen Anspruch auf Neuheit und all dies ist recht einfach Der terminologische Unterschied ist meiner Meinung nach nicht wirklich wichtig

Zusammenfassung

In diesem Artikel werden wir über zwei Arten von Funktionen sprechen (definiert im Bereich der reellen Zahlen): analytisch und Gitter.

1

, $$$F(x), G(x), ...$ , ($$$N_0$), $$$f_n, g_n, ...$. $$$A^\epsilon$.

2

, . , . ( ),

Wir werden eine Eins-zu-Eins-Entsprechung zwischen Funktionen aus diesen beiden Klassen herstellen. Wir werden auch neue Operationen für Gitterfunktionen einführen. Diese Operationen ähneln den "normalen" Operationen bei "normalen" Funktionen. Wir werden diese neuen Operationen durch Hinzufügen des Präfixes "epsilon" unterscheiden. Das "gewöhnliche" Derivat entspricht also dem Epsilon-Derivat , das gewöhnliche Produkt dem Epsilon-Produkt , die übliche Integration zur Epsilon-Integration usw. Wenn die Operation unverändert bleibt (wie im Fall von Summation und Subtraktion), ändert sich der Name nicht.

Eines der Hauptziele bei der Einführung dieser Operationen ist einfach - die Eigenschaften des abgeleiteten Produkts von Funktionen zu erhalten:

$$$(F(x)G(x))' = F'(x)G(x) + F(x)G'(x)$

Was ist bei Gitterfunktionen der Fall ($$$\in A^\epsilon$) wird aussehen wie

$$$\overset{\displaystyle\epsilon}{\nabla} (f_n \overset{\displaystyle\epsilon}{*}g_n) = \overset{\displaystyle\epsilon}{\nabla} f_n \overset{\displaystyle\epsilon}{*}g_n + f_n \overset{\displaystyle\epsilon}{*}\overset{\displaystyle\epsilon}{\nabla} g_n$

Wo $$$\overset{\displaystyle\epsilon}{\nabla}$ - linker Epsilon-Derivatoperator
$$$\overset{\displaystyle\epsilon}{*}$- Epsilon-Multiplikation

Dies ermöglicht es uns (in Analogie zum Beispiel zur Laplace-Transformation), eine neue Transformation einzuführen, die wir Epsilon-Transformation nennen werden . Dies gibt uns die Möglichkeit, im allgemeinen Fall nichtlineare integrale Differentialgleichungen in wiederkehrende Ausdrücke umzuwandeln und diese (numerisch bzw. analytisch) durch wiederkehrende Methoden zu lösen.

Bemerkung:

Das Gegenteil ist auch der Fall: Wir erhalten die Möglichkeit, Wiederholungsrelationen mit den Methoden integraler Differentialgleichungen zu lösen

Eine wichtige Tatsache in diesem Fall ist, dass wenn der Schritt der Gitterfunktion gegen Null geht ($$$\epsilon \to 0$), alle unsere Epsilon-Funktionen, Epsilon-Operationen und Wiederholungsgleichungen tendieren zu „gewöhnlichen“ Funktionen (analytisch rechts von Null), gewöhnlichen Operationen zwischen ihnen und gewöhnlichen Integral-Differential-Gleichungen.

Dies führt jedoch zu einer grundlegenden Frage: Ist die Epsilon-Multiplikation in unserer physischen Welt nicht „wahre“ Multiplikation (zumindest wenn es um Raum und Zeit geht)?

So spricht man zum Beispiel von Zeit mit einem ausreichend kleinen Schritt (zum Beispiel in der Größenordnung der Planck-Zeit)$$$t_p \sim 10^{-43}$ sec) Epsilon-Schrödinger-Gleichung c $$$\epsilon\sim t_p$ für temporäre Prozesse mit charakteristischer Zeit $$$t \gg t_p$ (oder im Frequenzbereich mit Frequenzen $$$\omega \ll 1/\epsilon$) liefert das gleiche Ergebnis wie die übliche Schrödinger-Gleichung, aber gleichzeitig wird natürlich die Zeitquantisierung eingeführt.

Im Prinzip ist ein ähnliches Argument für den Raum möglich.

Gitterfunktionen und Epsilon-Derivat

Gitterfunktion und eingestellt $$$A^\epsilon$

Gitterfunktionen sind Funktionen, die auf einem diskreten Satz von reellen Zahlen mit einem konstanten Schritt definiert sind. Wir werden nur Funktionen betrachten, die am Set definiert sind$$$\{0,\epsilon,2\epsilon,3\epsilon,\ldots\}$wo $$$\epsilon \in R$, $$$\epsilon>0$. So wäre zum Beispiel eine solche Funktion$$$cos(0.1k\pi)$wo $$$k$Ist eine nicht negative ganze Zahl. Dabei$$$\epsilon = 0.1\pi$. Wir bezeichnen die Menge solcher Funktionen mit$$$A^\epsilon$. Alle Gitterfunktionen, die wir unten betrachten werden, gehören zu dieser Menge$$$A^\epsilon$.

Beispiel für eine Gitterfunktion$$$\in A^\epsilon$

Funktion $$$cos(0.1k\pi)$wo $$$k \i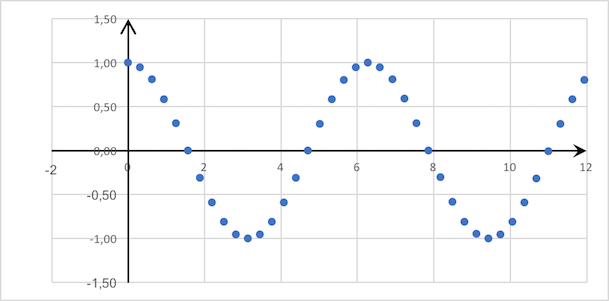n N_0$:



Epsilon-Derivat

Wir werden die Epsilon-Derivatfunktion nennen$$$f \in A^\epsilon$ beim $$$k$ folgenden Wert:

$$$f\overset{\displaystyle\epsilon}{'}_k = \overset{\displaystyle\epsilon}{\nabla}{f_k} = (f_{k+1} - f_k)/\epsilon$

Dementsprechend eine Funktion, deren Wert in $$$k$ für jeden $$$k$ entspricht der Epsilon-Ableitungsfunktion $$$f_n$ beim $$$k$Wir werden die Epsilon-Ableitungsfunktion aufrufen $$$f_n$ und bezeichnen als $$$f_n\overset{\displaystyle\epsilon}{'}$ (oder einfach $$$f\overset{\displaystyle\epsilon}{'}$)

Offensichtlich ist die Funktion$$$f^{\overset{\displaystyle\epsilon}{'}}\in$ $$$A^\epsilon$und daher kann die Epsilon-Differenzierung wieder darauf angewendet werden usw. Wir werden mit bezeichnen$$$^{\overset{\displaystyle\epsilon}{(n)}}$ $$$n$-Yu $$$\epsilon$-derivative Funktion. Es ist leicht durch Induktion zu beweisen, dass

$$$f^{\overset{\displaystyle\epsilon}{(n)}}_k=\displaystyle\frac{1}{\epsilon^n}\sum\limits_{j=0}^{n}C_{n}^{j}f_{k+j}(-1)^{n-j}$

Epsilon-Integration

Das der Epsilon-Differenzierung entgegengesetzte Verfahren wird als Epsilon-Integration bezeichnet. Funktion$$$g_n\in A^\epsilon$dessen Wert in $$$k$ für jeden $$$k$

$$$g_k=\epsilon\sum\limits^{k-1}_{i=0}f_i+C$

ruft epsilon primitive Funktionen auf $$$f$.

Epsilon-Derivat eines Produkts

Leider hat ein Epsilon-Derivat nicht die Eigenschaften eines regulären Derivats. So ist es zum Beispiel offensichtlich, dass im allgemeinen Fall

$$$(f_n g_n)^{\overset{\displaystyle\epsilon}{'}} = f_n^{\overset{\displaystyle\epsilon}{'}}g_n+g_n^{\overset{\displaystyle\epsilon}{'}}f_n +\epsilon f_n^{\overset{\displaystyle\epsilon}{'}} g_n^{\overset{\displaystyle\epsilon}{'}}\neq f_n^{\overset{\displaystyle\epsilon}{'}}g_n+g_n^{\overset{\displaystyle\epsilon}{'}}f_n$

Teil $$$\epsilon f_n^{\overset{\displaystyle\epsilon}{'}} g_n^{\overset{\displaystyle\epsilon}{'}}$unterscheidet diese "Ableitung" von der gewöhnlichen Ableitung des Produkts differenzierbarer Funktionen. Bei der Lösung nichtlinearer Differentialgleichungen mit numerischen Methoden ergibt sich ein zusätzlicher Fehler bei den Berechnungen.

Bemerkung:

Dieser zusätzliche Begriff führt insbesondere auch dazu, dass wir die übliche Taylor-Formel zur Erweiterung der Gitterfunktion in einer Reihe nicht anwenden können

Stellen wir uns nun vor, wir hätten dieses zusätzliche Mitglied nicht. Damit uns das geben kann?

Zumindest könnten wir einige Methoden zum Lösen von Differentialgleichungen anwenden, um Wiederholungsgleichungen zu lösen (Gleichungen mit Funktionen aus der Menge$$$A^\epsilon$) Zum Beispiel hätten wir uns zu einer Taylor-Reihe erweitert, wir könnten die Integration (Epsilon-Integration) in Teilen verwenden, Transformationen (Epsilon-Transformation) von Laplace anwenden. In Wirklichkeit ist jedoch alles noch interessanter, und dieser Artikel widmet sich diesem Thema.

Aber wie kann man dieses zusätzliche Element loswerden? Wir können zum Beispiel eine andere Multiplikation (Epsilon-Multiplikation) erstellen.

Das Grundproblem

Dies ist genau das Problem, dessen Lösung der gesamte Artikel ist.

Wir wollen eine Formel für das Epsilon-Produkt finden$$$p_k=(f\displaystyle\overset{\displaystyle\epsilon}{*}{g})_k$um die folgenden Anforderungen zu erfüllen:

• Die Eigenschaften der gewöhnlichen Multiplikation wären erfüllt, wie Kommutativität, Assoziativität, Verteilbarkeit, die Existenz einer Einheit (einzeln) und eines Nullelements (einzeln).
• für das Epsilon-Derivat des Epsilon-Produkts von Gitterfunktionen müssen wir die gleiche Formel haben wie für das Derivat des Produkts von (gewöhnlichen) differenzierbaren Funktionen, d.h.
  
  $$$\overset{\displaystyle\epsilon}{\nabla} (f_n \overset{\displaystyle\epsilon}{*}g_n) = \overset{\displaystyle\epsilon}{\nabla} f_n \overset{\displaystyle\epsilon}{*}g_n + f_n \overset{\displaystyle\epsilon}{*}\overset{\displaystyle\epsilon}{\nabla} g_n$
• während des Strebens $$$\epsilon \rightarrow 0$ (Gitterfunktionsschritt) Das Epsilon-Produkt sollte zum üblichen Produkt tendieren $$$F(x)G(x)$wo $$$F(x)$ und $$$G(x)$ jeweils Funktionen, zu denen Gitterfunktionen neigen $$$f_n$ und $$$g_n$ beim $$$\epsilon \rightarrow 0$, also:
  
  $$$F(x) = \lim\limits_{\epsilon \rightarrow 0, k\epsilon = x} f_k$
  $$$G(x) = \lim\limits_{\epsilon \rightarrow 0, k\epsilon = x} g_k$

Epsilon-Multiplikation

Die Funktion erfüllt alle diese Eigenschaften. $$$p_k$definiert als (alle drei Formeln sind äquivalent):

$$$p_k=(f\displaystyle\overset{\displaystyle\epsilon}{*}{g})_k=(\epsilon({{\overset{\displaystyle\epsilon}{\nabla}}_{f}}+{{\overset{\displaystyle\epsilon}{\nabla}}_{g}})+{\overset{\wedge}{I}})^k (f g)|_0$

$$$p_k = (f\displaystyle\overset{\displaystyle\epsilon}{*}{g})_k=\sum_{j=0}^{k}C_{k}^{j}\sum_{i=0}^{j}C_{j}^{i}{f^{\overset{\displaystyle\epsilon}{(i)}}}|_0{g^{\overset{\displaystyle\epsilon}{(j-i)}}}|_0$

$$$p_k=(f\displaystyle\overset{\displaystyle\epsilon}{*}{g})_k=\sum_{j+i+l=k}C_k^{j,i}f_ig_j(-1)^{l}$,
wo$$$C_{k}^{j,i}$ - Binomialkoeffizient von Newton: $$$C_{k}^{j,i}=\displaystyle\frac{k!}{j!i!l!}$, ($$$l+j+i=k$)

Hinweis

Um den Artikel nicht zu überladen, werden wir keine Beweise geben, aber die ersten beiden Eigenschaften sind leicht zu beweisen, die letzte ist nicht so offensichtlich

Betrachten Sie einige Beispiele, um sich mit der neuen Arbeit ein wenig vertraut zu machen.



Epsilon Taylor-Serie

Jetzt haben wir ein vollständiges Analogon zur Taylor-Erweiterung:
$$$f_k=f_0+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{1}}}{1!}{f\overset{\displaystyle\epsilon}{'}}_0+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{2}}}{2!}{f^{\overset{\displaystyle\epsilon}{(2)}}}_0+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{3}}}{3!}{f^{\overset{\displaystyle\epsilon}{(3)}}}_0+\ldots+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{k}}}{k!}{f^{\overset{\displaystyle\epsilon}{(k)}}}_0$

Wir werden diese Reihe die Epsilon-Reihe von Taylor nennen, und die Zerlegung selbst wird die Epsilon-Reihe in der Reihe von Taylor genannt.

Epsilon-Konvertierung

Definition (Epsilon-Transformation)

Lassen Sie$$$\exists x_0 >0$ so dass am Set $$$[0,x_0)$ Taylor-Funktionsreihe $$$F(x)$in der rechten Nachbarschaft von Null konvergiert zur Funktion selbst. Dann die Funktion$$$F(x)$Wir werden die analytische Funktion rechts bei Null aufrufen. Dann die Funktionen$$$F$ und $$$f\in A^\epsilon$wird epsilon-konjugiert genannt, wenn für eine ganze Zahl oder Null$$$i$ $$$i$rechte Ableitung $$$F$ bei Null ist gleich $$$i$Epsilon-Ableitungsfunktion $$$f$ bei Null.
$$$F^{(i)}|_{+0}=f^{\overset{\displaystyle\epsilon}{(i)}}_0, \forall i \in N_0$

Funktion $$$f$dann werden wir das Epsilon-Bild aufrufen $$$F$ oder falls diese Funktion einen Namen hat (zum Beispiel cos), nennen wir epsilon einfach "Funktionsname" (zum Beispiel epsilon-cosine) und bezeichnen ihn als $$$\epsilon$`` Funktionsbezeichnung '' ($$$\epsilon$cos). Funktion$$$F$Wir nennen das epsilon-inverse Bild der Funktion$$$f$.




Epsilon-Transformationsoperationen

In dieser Tabelle und in der folgenden Funktion$$$F(x)$ und $$$f_n$, und auch $$$G(x)$ und $$$g_n$ - gepaartes Epsilon-Konjugat, d.h.

$$$F(x) \overset{\epsilon}\to f_n$
$$$G(x) \overset{\epsilon}\to g_n$

Dann werden die Operationen (als Ergebnis der Epsilon-Konvertierung) wie folgt konvertiert:

$$$F(x) \equiv G(x)$ $$$\overset{\epsilon} {\to}$ $$$f_n \equiv g_n$

$$$F(x) + G(x)$ $$$\overset{\epsilon} {\to}$ $$$f_n + g_n$

$$$F(x) G(x)$ $$$\overset{\epsilon} {\to}$ $$$f_n \displaystyle\overset\epsilon{*} g_n$

$$$F'(x)$ $$$\overset{\epsilon} {\to}$ $$$f \displaystyle\overset\epsilon{'}_n$

$$$\int F(x)dx$ $$$\overset{\epsilon} {\to}$ $$$\epsilon\sum\limits^{k-1}_{i=0}f_i$(Epsilon-Primitiv)

Epsilon-Transformation einiger analytischer Funktionen

$$$F(x) \equiv \lambda$ $$$\overset{\epsilon} {\to}$ $$$f_n \equiv \lambda$

$$$\lambda F(x)$ $$$\overset{\epsilon} {\to}$ $$$\lambda f_n$

$$$x^i$ $$$\overset{\epsilon} {\to}$ $$$(k\epsilon)^{\overset{\displaystyle\epsilon}{i}}=i!C_k^i\epsilon^i$

$$$\exp(\lambda x)$ $$$\overset{\epsilon} {\to}$ $$$\epsilon exp(\lambda x)_k=(1+\lambda \epsilon)^k$

$$$\cos(\lambda x)$ $$$\overset{\epsilon} {\to}$ $$$\epsilon{\cos(\lambda x)}_k=\frac{1}{2}((1+i\lambda\epsilon)^k+(1-i\lambda\epsilon)^k)$

$$$\sin(\lambda x)$ $$$\overset{\epsilon} {\to}$ $$$\epsilon{\sin(\lambda x)}_k=\frac{1}{2i}((1+i\lambda \epsilon)^k-(1-i\lambda \epsilon)^k)$

$$$(1 + \lambda x)^{-1}$ $$$\overset{\epsilon} {\to}$ $$$(1+\lambda x)^{\overset{\displaystyle\epsilon}{-1}}=1-\lambda x +\lambda^2 x^{\overset{\displaystyle\epsilon}{2}}-\lambda^3x^{\overset{\displaystyle\epsilon}{3}}+...$ (zum $$$|\lambda x| < 1$A)

Taylor-Epsilon-Expansion

$$$f_k = (1 + \epsilon \overset{\epsilon}{\nabla})^k f|_{k=0}=f_0+\displaystyle\frac{(\epsilon k)^{\overset{\displaystyle\epsilon}{1}}}{1!}{f\overset{\displaystyle\epsilon}{'}}_0+\displaystyle\frac{(\epsilon k)^{\overset{\displaystyle\epsilon}{2}}}{2!}{f^{\overset{\displaystyle\epsilon}{(2)}}}_0+\displaystyle\frac{(\epsilon k)^{\overset{\displaystyle\epsilon}{3}}}{3!}{f^{\overset{\displaystyle\epsilon}{(3)}}}_0+\ldots+\displaystyle\frac{(\epsilon k)^{\overset{\displaystyle\epsilon}{k}}}{k!}{f^{\overset{\displaystyle\epsilon}{(k)}}}_0$

Diese Formel wird offensichtlich, wenn wir feststellen, dass der Operator $$$(1 + \epsilon \overset{\epsilon}{\nabla})^i$ ist ein Offset-Operator an $$$i$ Schritte:

$$$(1 + \epsilon \overset{\epsilon}{\nabla})^i f_k = f_{k+i}$

Epsilon Laplace-Transformation

Wir können auch die Epsilon Laplace-Transformation einführen und sie sowie die übliche Laplace-Transformation in Bezug auf Gitterfunktionen verwenden$$$\in A^\epsilon$Dies würde jedoch den Rahmen dieses Artikels sprengen.

Epsilon-Transformationen für trigonometrische Formeln

In Anbetracht des Vorstehenden können wir beispielsweise Analoga trigonometrischer Formeln schreiben

$$${\epsilon{\cos(x)}}^{\overset{\displaystyle\epsilon}{2}}+{\displaystyle\epsilon{\sin(x)}}^{\overset{\displaystyle\epsilon}{2}}\equiv 1$

$$${\epsilon{\cos(x)}}{\overset{\displaystyle\epsilon}{'}}\equiv-\epsilon{\sin(x)}$

$$${\epsilon{\sin(x)}}{\overset{\displaystyle\epsilon}{'}}\equiv\epsilon{\cos(x)}$

$$${\epsilon{\cos(\alpha+\beta)}}\equiv{\epsilon{\cos(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\cos(\beta)}}-{\epsilon{\sin(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\sin(\beta)}}$

$$${\epsilon{\cos(\alpha-\beta)}}\equiv{\epsilon{\cos(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\cos(\beta)}}+{\epsilon{\sin(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\sin(\beta)}}$

$$${\epsilon{\sin(\alpha+\beta)}}\equiv{\epsilon{\sin(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\cos(\beta)}}+{\epsilon{\cos(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\sin(\beta)}}$

$$${\epsilon{\sin(\alpha-\beta)}}\equiv{\epsilon{\sin(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\cos(\beta)}}-{\epsilon{\cos(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\sin(\beta)}}$

Dennoch haben der Epsilon-Cosinus und der Epsilon-Sinus im Gegensatz zum üblichen Cosinus und Sinus kein wichtiges Merkmal - sie sind nicht periodisch. Ja wirklich,

$$$\epsilon{\cos(\omega t)}_k=\frac{1}{2}((1+i\omega \epsilon)^k+(1-i\omega \epsilon)^k)=\left({\sqrt{1+(\omega \epsilon)^2}}\right)^k \cos{(k(arctg(\omega \epsilon)))}$

$$$\epsilon{\cos(\omega t)}_{\frac{t}{\epsilon}}=\left({{1+\omega^2 \epsilon^2}}\right)^{\frac{t}{2\epsilon}}\cos{(t \displaystyle \frac{arct(\omega \epsilon)}{ \epsilon})}$

Ebenfalls
$$$\epsilon{sin(\omega t)}_{\frac{t}{\epsilon}}=\left({{1+\omega^2 \epsilon^2}}\right)^{\frac{t}{2\epsilon}}\sin{(t \displaystyle \frac{arctg(\omega \epsilon)}{ \epsilon})}$

gleichzeitig funktioniert $$$sin( t(arctg(\omega \epsilon)/\epsilon))$ und $$$\cos(t(arctg(\omega\epsilon/)\epsilon))$ - periodische Funktionen mit einer Periode $$$2\pi\epsilon/arctg(\omega \epsilon)$. Funktioniert also$$$\epsilon{\cos(x)}$ und $$$\epsilon{\sin(x)}$ - nichtperiodische Funktionen mit Nullen an Punkten $$$(\pi/2+\pi n)\epsilon/arctg(\omega \epsilon)$ und $$$\pi n\epsilon/arctg(\omega \epsilon)$ dementsprechend ist in diesem Fall der "Bereich" zwischen den Minima und Maxima, wenn er weggetragen wird $$$t$ erhöht sich als $$$({1+\omega^2\epsilon^2})^{\frac{t}{2\epsilon}}$.

Bemerkung

Dementsprechend haben wir für den Epsilon-Exponenten

$$$\epsilon{exp(i\omega t)}_{\frac{t}{\epsilon}}=\left({{1+\omega^2 \epsilon^2}}\right)^{\frac{t}{2\epsilon}}\exp{(i \displaystyle \frac{arctg(\omega \epsilon)}{ \epsilon}t)}$

Beispiele für die Lösung von Differentialgleichungen mit der Epsilon-Mapping-Methode

Epsilon-Mapping-Eigenschaften als ε → 0

Die umgekehrte Epsilon-Konvertierung kann einfach durch Anweisung erfolgen $$$\epsilon \to 0$

Dies kann strenger in Form eines Satzes formuliert werden, den ich ohne Beweis geben werde.

Satz

Let Funktionen$$$F$ und $$$f$ - Epsilon-Konjugat für jeden $$$\epsilon$. Dann beim Streben$$$\epsilon \to 0$, unter der Vorraussetzung, dass $$$k\epsilon=const=a\in(0,x_0)$ (Wo $$$x_0$ hat die gleiche Bedeutung wie in der Definition der Epsilon-Zuordnung), der Wert $$$f_k$ am Set $$$(0,x_0)$ engagiert für $$$F(a)$, also

$$$\lim\limits_{\epsilon \to0, k\epsilon=a}f(k\epsilon)=F(a)$

Nicht analytische Funktionen

Epsilon-Produkt und Diskretion der Raumzeit

All dies führt zu einer grundlegenden Frage: a Ist Epsilon-Multiplikation nicht "wahre" Multiplikation in unserer physischen Welt (zumindest wo es um Raum oder Zeit geht)?

Betrachten Sie zum Beispiel die eindimensionale Schrödinger-Gleichung:

$$$i\hbar\frac{\partial}{\partial t}\Psi(x,t)=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\Psi(x,t) + U(x,t)\Psi(x,t)$

Diese Gleichung setzt die Kontinuität der Raum-Zeit und die Möglichkeit eines infinitesimalen Wertes voraus $$$\Delta x$ und $$$\Delta t$(Dies wird implizit akzeptiert, wenn wir Differenzierung verwenden). Wenn wir über Zeit sprechen, impliziert dies unendliche Energie, was modernen Vorstellungen über das Universum widerspricht.

Um das Argument nicht zu komplizieren, betrachten wir den Fall, wenn$$$U$ unabhängig von $$$t$. In diesem Fall$$$\Psi(x,t)$ kann geschrieben werden als:

$$$\Psi(x,t) = \psi(x)\exp(-iEt/\hbar)$

Aber $$$\exp(-iEt/\hbar)$ Ist eine analytische Funktion, was bedeutet, dass wir unseren Ansatz darauf anwenden können, dh wir können eine Epsilon-Transformation (relativ zur Zeit) unserer ursprünglichen Schrödinger-Gleichung durchführen und wir erhalten

$$$i\hbar\overset{\displaystyle\epsilon}{\nabla}\overset{\displaystyle\epsilon}\Psi(x,t)=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\overset{\displaystyle\epsilon}\Psi(x,t) + U(x)\overset{\displaystyle\epsilon}\Psi(x,t)$

$$$\overset{\displaystyle\epsilon}\Psi(x,t) = \psi(x)\epsilon exp(-iEt/\hbar)$

Dabei

$$$\overset{\displaystyle\epsilon}\Psi(x,t) \overset{\epsilon \to 0}{\to}\Psi(x,t)$

Das heißt, mit einem sehr kleinen Zeitschritt (Zeitquantum) $$$\epsilon$Was für unsere Berechnungen nicht wesentlich ist, werden wir den Unterschied zwischen der Lösung der (gewöhnlichen) Schrödinger-Gleichung und der Lösung der Epsilon-Schrödinger-Gleichung nicht sehen.

Dies bedeutet jedoch, dass wir nicht wirklich sagen können, welche Arbeit „wahr“ (von der Natur „verwendet“) ist - unser gewöhnliches oder Epsilon-Produkt (mit einer relativ kleinen Quantisierung der Zeit).

Darüber hinaus haben wir im Fall des Epsilon-Produkts (und dementsprechend der Schrödinger-Epsilon-Gleichung und ihrer Epsilon-Wellen-Lösung) eine offensichtliche Plus-Zeit-Quantisierung, die natürlich wird, und wir stoßen nicht auf das Erfordernis einer unendlichen Energie. Tatsächlich haben wir dieselbe Gleichung mit denselben Lösungen, aber gleichzeitig eliminieren wir natürlich die Notwendigkeit der Annahme der Kontinuität der Zeit.

- , , , , . , . , , $$$\Delta x \ll \delta_x$ / $$$\Delta t \ll \delta_t$ . , , . « » , $$$\Delta x \gg \delta_x$ / $$$\Delta t \gg \delta_t$. , . -, , $$$\epsilon$ — $$$\Delta x$ / $$$\Delta t$Wenn es immer noch sinnvoll ist, über Zeit und / oder Raum zu sprechen (ungefähr ist dies die durchschnittliche Größe des „Spots“).

Wie zu überprüfen?

Also, wenn die Zeit mit einem "Schritt" diskret ist $$$\epsilon$und die "wahre" Multiplikation ist die Epsilon-Multiplikation mit einem Schritt der Zeitdiskriminierung. Wie kann dies dann manifestiert werden? Ist es möglich, einen Gedanken oder ein reales Experiment aufzustellen und zu verstehen, welche Arbeit „wahr“ ist und welcher Schritt (Quantum) verwendet wird?

Einige Schätzungen können gegeben werden, um zu verstehen, wie stark sich unsere Vorstellungen von der Welt ändern würden, wenn die „Epsilon-Multiplikation“ (anstelle der gewöhnlichen Multiplikation) „wahr“ wäre.

Erinnere dich daran

$$$\epsilon{exp(i\omega_0 t)}_{\frac{t}{\epsilon}}=\left({{1+\omega_0^2 \epsilon^2}}\right)^{\frac{t}{2\epsilon}}\exp{(i \displaystyle \frac{arctg(\omega_0 \epsilon)}{ \epsilon}t)}$

Dann für $$$\omega_0\epsilon \ll 1$ wir haben:

• Die Frequenz unterscheidet sich von der Frequenz der Sinuswelle $$$\omega_0$ und wird gleich sein
  
  $$$\omega = \displaystyle \frac{arctg(\omega_0 \epsilon)}{ \epsilon} \approx \omega_0(1 - \displaystyle\frac{\omega_0^2\epsilon^2}{3})$
• Die Amplitude nimmt zu als
  
  $$$(1+(\omega_0\epsilon)^2))^{\frac{t}{2\epsilon}} \approx 1 + \displaystyle\frac{t\omega^2_0\epsilon}{2}$

Lassen Sie uns grob einschätzen, ob wir diesen Unterschied feststellen können.

Beispiel 1. Änderungen während des Lebens des Universums

Angenommen, unsere zeitliche Diskretion ist vergleichbar mit der Planck-Zeit:

$$$t_p \approx 10^{−43 }$sek

Lebensdauer des Universums:

$$$t_{u} \approx 10^{17}$sek

Finden Sie für welche Frequenzen$$$\omega_0$ Während der Lebensdauer des Universums könnte sich die Amplitude der Schwingungen beispielsweise um 0,5% ändern.

$$$t_u t_p\omega^2_0 = 10^{-2}$

$$$\omega_0 = \displaystyle\frac{10^{-1}}{\sqrt{t_ut_p}} = 10^{-1}10^{13} = 10^{12}$rad / s

Dies bedeutet, dass für Frequenzen in der Größenordnung von 1 THz (oder für Teilchen mit Energie$$$10^6$eV) Während der Lebensdauer des Universums würde sich die Amplitude (Wellenfunktion) um etwa ein Prozent (Ordnung) ändern. Das heißt, es ist klar, dass wir es zumindest im normalen Leben überhaupt nicht sehen können.

Beispiel 2. Änderungen pro Sekunde

Lassen Sie uns abschätzen, wie oft sich die Amplitude der Wellenfunktion eines Teilchens mit ultrahoher Energie ändert$$$10^{18}$ eV in einer Sekunde.

$$$10^{18}$ ev entspricht in der Reihenfolge $$$10^{24}$ Hz

$$$(1+(\omega_0 t_p)^2))^{\frac{1}{2t_p}} \approx 10^{48}10^{-43} = 10 ^5$

Das heißt, in einer Sekunde erhöht sich die Amplitude der Wellenfunktion eines solchen Teilchens um das 100.000-fache (Ordnung).

Es sieht substanziell aus. Aber wie erkennt man das? Tatsache ist, dass die physikalische Bedeutung nicht die Wellenfunktion selbst hat, sondern$$$\Psi\Psi^*$und im Falle eines Epsilon-Bildes wird es sein $$$\overset{\epsilon}\Psi \displaystyle\overset{\displaystyle \epsilon}{*}\overset{\epsilon}\Psi$. Aber

$$$\epsilon exp(-iEt/\hbar) \overset{\displaystyle\epsilon}{*} \epsilon exp(iEt/\hbar) = 1$

Dies deutet darauf hin, dass sich nur eine Größe, die eine physikalische Bedeutung hat, nicht ändert, und dieser Ansatz wird es uns nicht ermöglichen, die gestellte Frage zu beantworten.

Antworten auf Fragen aus Kommentaren