(Fast) Farben automatisch generieren

Am 8. März hatte ich eine Implementierung des automatisierten Zeichnens von Oberflächen mit Splines - warum nicht einen Artikel mit Farben schreiben?

Es stellte sich ungefähr so ​​heraus:



Es wird mehr unter dem Schnitt geben, kümmere dich um den Verkehr.

Der Algorithmus, kubische Kurven macht beschrieben wurde zuvor . Hier werden wir versuchen, es anzuwenden, um etwas Blumenartiges zu erhalten. Das einzige Problem ist die Auswahl der Eingabedaten.
Die Eingabedaten sind eine Reihe von Punkten mit Koordinaten im dreidimensionalen Raum und eine Reihe von Verbindungen zwischen ihnen, so dass dieses Design topologisch einer Box wie dieser entsprechen sollte: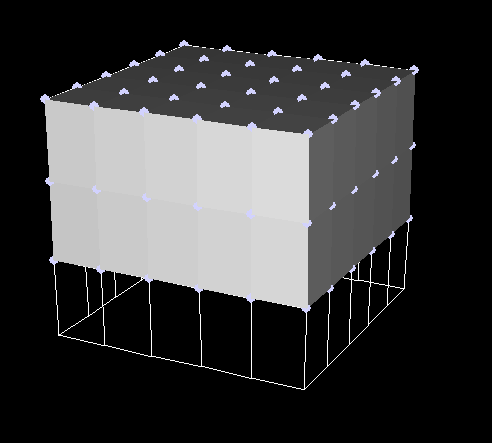



(am Ende sollte es so sein :)



Damit die kubischen Oberflächen, wenn sie auf den Kern gespannt werden, wie eine Blume aussehen Es ist notwendig, die Punkte symmetrisch auf den Kreisen anzuordnen, die um die Mitte der Blume herum umschrieben sind. Um dieses Problem zu lösen, wurde eine Variation der "Breitensuche" angewendet.

Allen Gewichtspunkten zuordnen. Zuerst weisen wir den Extrempunkten die Gewichte 0 und 1 zu (zwei identische Gewichte sollten nicht in der Nähe sein). Dies sind die Ränder der „Blütenblätter“, 0 - die fernen, 1 - die nahen (die „Blütenblätter“ stehen in Anführungszeichen, da es keine Unterteilung in Blütenblätter als solche gibt). Wiegen Sie weiter, indem Sie ungewichteten Nachbarn mit dem Gewicht n das Gewicht n + 2 zuweisen.

Gewichtete Box: Wählen Sie als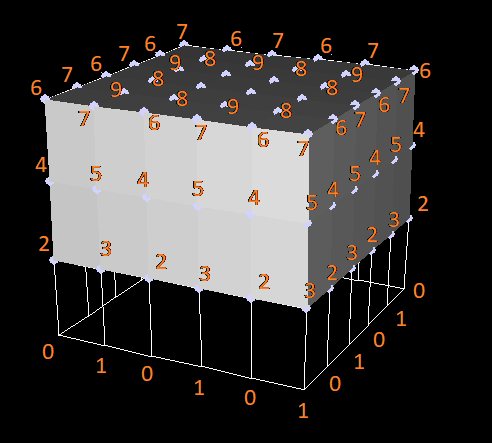



nächstes zufällig den Abstand r von der Mitte der Blume für jede Gewichtsklasse aus.
Die Logik hier lautet wie folgt: Je größer das Gewicht, desto näher muss der Punkt in die Mitte verschoben werden, und Ungleichungen sollten erfüllt sein:

$$

$$r_0 > r_2 > r_4> ... > r_{2n};\ \ r_1 > r_3 > ... > r_{2n+1};\ \ r_0 > r_1$$

Dabei ist r der Abstand von der Mitte der Blume zu Punkten mit dem entsprechenden Gewicht. Gerade Gewichte sind für den zentralen Teil des „Blütenblatts“ verantwortlich, ungerade Gewichte sind für die Kanten des „Blütenblatts“ verantwortlich.

Um Punkte auf Kreisen (und nicht auf Kugeln) anzuordnen, müssen wir auch zufällig Z-Koordinaten so auswählen, dass z_n <r_n ist (wenn der Mittelpunkt der Blume auf der Koordinate Null liegt).



Im nächsten Schritt müssen wir die Winkel für die Position der Punkte auf dem Kreis kennen:

$$

$$\ m_n - \ \ \ \ n, \ \alpha_n = 2\cdot \pi/m_n$$

und dann die Koordinaten für den i-ten Gewichtspunkt n, wenn er gerade ist:

$$

$$x_i = \sqrt{r_n^2-z_n^2}\cdot cos(i\alpha_n)$$

$$

$$y_i = \sqrt{r_n^2-z_n^2}\cdot sin(i\alpha_n)$$

für ungerade:

$$

$$x_i = \sqrt{r_n^2-z_n^2}\cdot cos(i\alpha_n+\alpha_n/2)$$

$$

$$y_i = \sqrt{r_n^2-z_n^2}\cdot sin(i\alpha_n+\alpha_n/2)$$

Außerdem ist die Reihenfolge, in der wir die Punkte aufnehmen, wichtig - sie müssen „Nachbarn“ sein.



Nach all diesen Manipulationen wird eine sternförmige Struktur erhalten, an der Keile gezogen werden können.

(Draufsicht, Isometrie, Splines)





Solche Kelchblätter können auf 100.500 randomisiert werden, aber um geeignete auszuwählen, mehrere Blumen zu machen, Farben und Kernparameter manuell besser auszuwählen, erfolgt die Erzeugung daher halbautomatisch.

(Ansicht der Montagesoftware)













Herzlichen Glückwunsch zum Internationalen Frauentag an die schöne Hälfte der Habrasociety! Ich hoffe du warst schön.