🥘 🌷 👎🏼 Julia und zellulare Automaten 🥖 🧛🏻 🚤

Heute werden wir eine farbenfrohe Reise durch die Welt der zellularen Automaten unternehmen, gleichzeitig einige Tricks ihrer Implementierung studieren und versuchen zu verstehen, was sich hinter dieser Schönheit verbirgt - ein merkwürdiges Spiel für einen müßigen Geist oder ein tiefes philosophisches Konzept, das bei vielen Modellen Anklang findet.

Zum Üben und zum besseren Verständnis sollten Sie versuchen, die folgenden Algorithmen selbst zu implementieren. Wenn Sie faul oder nur aus Interesse sind, können Sie mit verschiedenen Implementierungen herumspielen:

Golly — . .
Lenia — "".
. ,

— . , 0 1, , . . , . , . , 256 ( 8- ).

, .

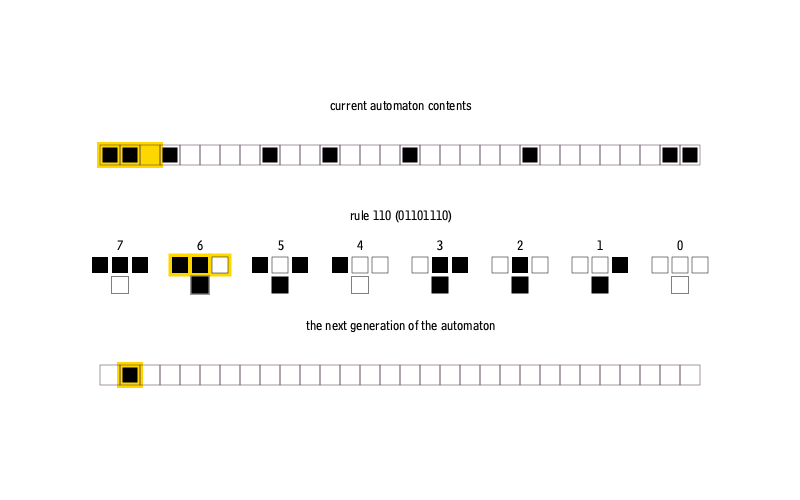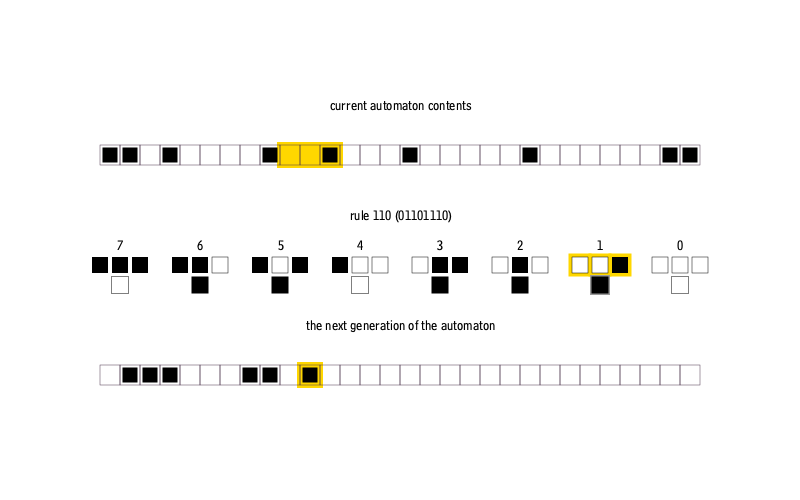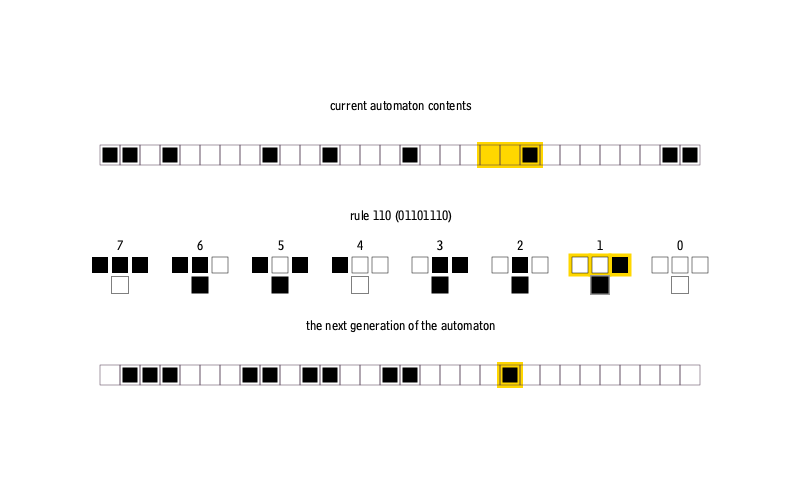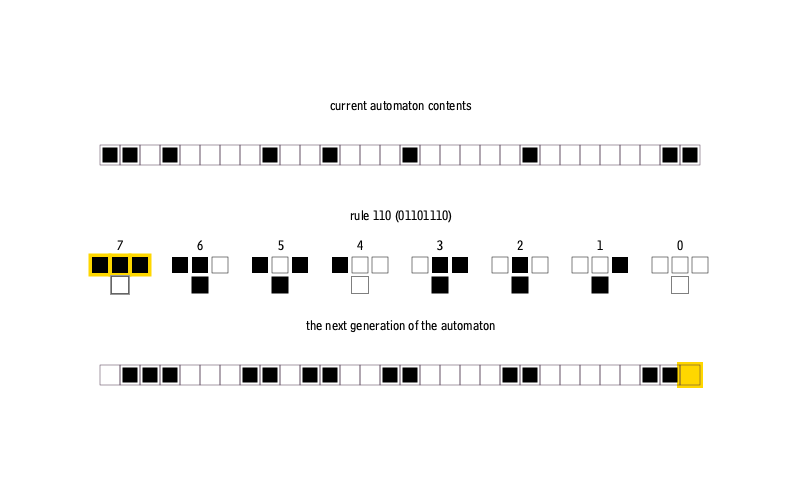
using Pkg
pkgs = ["Images", "ColorSchemes", "FFTW"]

for p in pkgs
    Pkg.add(p)
end

using Images, ColorSchemes, FFTW, LinearAlgebra: kron
using Random: bitrand
cd("C:\\Users\\User\\Desktop\\Mycop")

0 255 ( ). , . , , :

# , ,    
function cellauto( n::Int64, m::Int64, rule::Int64, s::Int64 = 1 )

    ptrn = digits(Bool, rule, base = 2, pad = 8)
    bt = [ bitstring(i)[end-2:end] for i = 0:7 ]
    d = Dict( bt[i] => ptrn[i] for i = 1:8 ) # 

    M = falses(n,m)
    M[1,m ÷ 2] = true
    #M[1,:] .= bitrand(m)
    for i = 1:n-1, j = 2:m-1
        key = "$(M[i, j-1]*1)$(M[i, j]*1)$(M[i, j+1]*1)"
        M[i+1,j] = d[key]
    end
    kron(M, ones(Int,s,s) ) #  
end

M0 = cellauto(100, 200, 30, 4)
Gray.( M0 )

30, . , , . , - : , … , . :

Arr = cellauto.(40, 40, [0:23;], 2);
Imgs = [ Gray.(a) for a in Arr ]
reshape(Imgs, 4,6)

, . :

Luxor, .

"" — ( ) . , , : , ( ) .

: , , ( !) . , , , . . . , , , , , , . "" .

, , . , , .

function makefilter(N::Int64)
    filter = zeros(Complex, N, N);
    IDX(x, y) = ( (x + N) % N ) + ( (y+N) % N ) * N + 1
        filter[IDX(-1, -1)] = 1. ;
        filter[IDX( 0, -1)] = 1. ;
        filter[IDX( 1, -1)] = 1. ;
        filter[IDX(-1,  0)] = 1. ;
        filter[IDX( 1,  0)] = 1. ;
        filter[IDX(-1,  1)] = 1. ;
        filter[IDX( 0,  1)] = 1. ;
        filter[IDX( 1,  1)] = 1. ;

    return fft( real.(filter) )
end

function fftlife(N = 16, steps = 100, dx = 0, glider = true)

    if glider
        state = falses(N, N)
        state[4,5] = state[5,6] = state[6,6] = true
        state[6,5] = state[6,4] = true
    else
        state = bitrand(N, N)
    end

    filter = makefilter(N)

    for i in 1:steps
        tmp = fft( real.(state) ) # forward
        tmp .*= filter

        summ = ifft(tmp) # reverse

        for i in eachindex(state)
            t = round( Int, real(summ[i]) ) >> dx
            state[i] = ( state[i] ? t == 2 || t == 3 : t == 3 )
        end
        save("KonLife_$(N)x$(N)_$i.png", kron( Gray.(state), ones(8,8) ) )
    end

end

fftlife(16, 60)

— , ( ). , "" .

\frac{d f (x, t)}{d t} = S (N (x, t), M (x, t)) - f (x, t) S (n, m) = σ_{n} (σ_{m} (b_{1}, b_{2}), σ_{m} (d_{1}, d_{2})) M (x, t) = \frac{1}{π h^{2}} \int_{0 \leq | y | \leq h} f (x - y, t) d y N (x, t) = \frac{1}{8 π h^{2}} \int_{0 \leq | y | \leq 3 h} f (x - y, t) d y

$\frac{df(x,t)}{dt} = S\left(N(x,t),M(x,t) \right ) - f(x,t) \\ \\ S(n,m) = \sigma_n\left(\sigma_m(b_1, b_2), \sigma_m(d_1,d_2)\right)\\ M(x,t) = \frac{1}{\pi h^2} \int\limits_{0\le |y| \le h} f(x-y, t) dy \\ N(x,t) = \frac{1}{8\pi h^2} \int\limits_{0\le |y| \le 3h} f(x-y, t) dy$

1 0, , , .

Anfangsbedingungen

function clamp(x)
    y = copy(x)
    y[x.>1] .= 1
    y[x.<0] .= 0
    y
end

function func_linear(X, a, b)
    Y = [ (x-a + 0.5b)/b for x in X ]

    Y[X.<a-0.5b] .= 0
    Y[X.>a+0.5b] .= 1
    return Y
end

function splat!(aa, ny, nx, ra)
    x = round(Int, rand()*nx ) + 1
    y = round(Int, rand()*ny ) + 1
    c = rand() > 0.5

    for dx = -ra:ra, dy = -ra:ra
        ix = x+dx
        iy = y+dy
        if ix>=1 && ix<=nx && iy>=1 && iy<=ny
            aa[iy,ix] = c
        end
    end
end

function initaa(ny, nx, ra)
    aa = zeros(ny, nx)
    for t in 0:((nx/ra)*(ny/ra))
        splat!(aa, ny, nx, ra);
    end
    aa
end

Sigmoid

func_smooth(x::Float64, a, b)  = 1 / ( 1 + exp(-4(x-a)/b) ) 

sigmoid_a(x, a, ea) = func_smooth(x, a, ea)
sigmoid_b(x, b, eb) = 1 - sigmoid_a(x, b, eb)
sigmoid_ab(x, a, b, ea, eb) = sigmoid_a(x, a, ea) * sigmoid_b(x, b, eb)
sigmoid_mix(x, y, m, em) = x - x * func_smooth(m, 0.5, em) + y * func_smooth(m, 0.5, em)

function snm(N, M, en, em, b1, b2, d1, d2)

    [ sigmoid_mix( sigmoid_ab(N[i,j], b1, b2, en, en), 
                   sigmoid_ab(N[i,j], d1, d2, en, en), M[i,j], em ) 
                    for i = 1:size(N, 1), j = 1:size(N, 2) ]
end

Hauptfunktion

function smoothlife(NX = 128, NY = 128, tfin = 10, scheme = 1)

    function derivative(aa)
        aaf = fft(aa)
        nf = aaf .* krf
        mf = aaf .* kdf
        n = real.(ifft(nf)) / kflr # irfft
        m = real.(ifft(mf)) / kfld
        2snm(n, m, alphan, alpham, b1, b2, d1, d2) .- 1
    end

    ra = 10
    ri = ra/3
    b = 1
    b1 = 0.257
    b2 = 0.336
    d1 = 0.365
    d2 = 0.551
    alphan = 0.028
    alpham = 0.147

    kd = zeros(NY,NX)
    kr = zeros(NY,NX)
    aa = zeros(NY,NX)

    x = [ j - 1 - NX/2 for i=1:NY, j=1:NX ]
    y = [ i - 1 - NY/2 for i=1:NY, j=1:NX ]

    r = sqrt.(x.^2 + y.^2)
    kd = 1 .- func_linear(r, ri, b) # ones(NY, NX)
    kr = func_linear(r, ri, b) .* ( 1 .- func_linear(r, ra, b) )
    #aa = snm (ix/NX, iy/NY, alphan, alpham, b1, b2, d1, d2);
    kflr = sum(kr)
    kfld = sum(kd)
    krf = fft(fftshift(kr))
    kdf = fft(fftshift(kd))

    #for td in 2 .^(10:-1:3)
    for td = 64

        aa = initaa(NY,NX,ra)
        dt = 1/td;
        l = 0
        nx = 0
        for t = 0:dt:tfin
# 1=euler  2=improved euler  3=adams bashforth 3  4=runge kutta 4
            if scheme==1

                aa += dt*derivative(aa)

            elseif scheme==2

                da = derivative(aa);
                aa1 = clamp(aa + dt*da)
                for h = 0:20
                    alt = aa1
                    aa1 = clamp(aa + dt*(da + derivative(aa1))/2)
                    if maximum(abs.(alt-aa1))<1e-8 
                        break
                    end
                end
                aa = copy(aa1)

            elseif scheme==3

                n0 = 1+mod(l,3)
                n1 = 1+mod(l-1,3)
                n2 = 1+mod(l-2,3)

                f = zeros(NY, NX, 3) # ?
                f[:,:,n0] = derivative(aa)
                if l==0
                    aa += dt*f[:,:,n0]
                elseif l==1
                    aa += dt*(3*f[:,:,n0] - f[:,:,n1])/2
                elseif l>=2
                    aa += dt*(23*f[:,:,n0] - 16*f[:,:,n1] + 5*f[:,:,n2])/12
                end

            elseif scheme==4

                k1 = derivative(aa)
                k2 = derivative(clamp(aa + dt/2*k1))
                k3 = derivative(clamp(aa + dt/2*k2))
                k4 = derivative(clamp(aa + dt*k3))
                aa += dt*(k1 + 2*k2 + 2*k3 + k4)/6

            end

            aa = clamp(aa)

            if t >= nx
                save("$(scheme)\\$(td)_$t.png", Gray.(kron(aa, ones(2, 2) ) ) )
                nx += 1;
            end

            l += 1;
        end

    end     # for td
end

@time smoothlife(256, 256, 20, 3)

, . , . .

— , , . — .

, , , :

— $90^\circ$ , , .
— $90^\circ$ , , .

rosetta code , :

function ant(width, height)
    y, x = fld(height, 2), fld(width, 2)
    M = trues(height, width)

    dir = im
    for i in 0:1000000
        x in 1:width && y in 1:height || break
        dir *= M[y, x] ? im : -im
        M[y, x] = !M[y, x]
        x, y = reim(x + im * y + dir)
        i%100==0 && save("LR//zLR_$i.png", Gray.( kron(M,ones(4,4) ) ) )
    end

    Gray.(M)
end

ant(100, 100)

, . — . !

function ant(width, height, comnds;
        steps = 10, cxema = reverse(ColorSchemes.hot), 
        savevery = 100, pixfactor = 20)

    ma3x2pix() = [ clrs[k%n+1] for k in M ]
      bigpix() = kron( ma3x2pix(), ones(Int64,m,m) )
    save2pix(i) = save("$(comnds)_$i.png", bigpix() )

    m = pixfactor
    n = length(comnds)
    colorsinscheme = length(cxema)
    M = zeros(Int64, height, width)
    y, x = fld(height, 2), fld(width, 2)

    st = colorsinscheme ÷ n
    clrs = [ cxema.colors[i] for i in 1:st:colorsinscheme ]

    dir = im
    for i in 0:steps
        x in 1:width && y in 1:height || (save2pix(i); break)
        j = M[y, x] % n + 1
        dir *= comnds[j] == 'L' ? -im : im
        M[y, x] += 1
        x, y = reim(x + im * y + dir)

        i % savevery==0 && save2pix(i)
    end
    ma3x2pix()
end

@time ant(16, 16, "LLRR", steps = 100, savevery = 1, pixfactor = 20)

, !

LLRR

. , ? ?..

# http://rosettacode.org/wiki/Mandelbrot_set
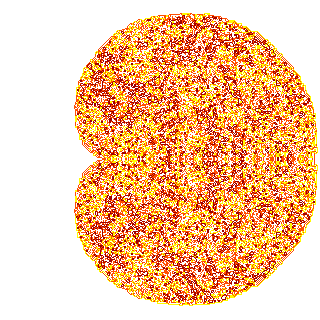
function hsv2rgb(h, s, v)
    c = v * s
    x = c * (1 - abs(((h/60) % 2) - 1) )
    m = v - c

    r,g,b =
        if h < 60
            (c, x, 0)
        elseif h < 120
            (x, c, 0)
        elseif h < 180
            (0, c, x)
        elseif h < 240
            (0, x, c)
        elseif h < 300
            (x, 0, c)
        else
            (c, 0, x)
        end

    (r + m), (b + m), (g + m)
end

function mandelbrot()

    w, h = 1000, 1000

    zoom  = 1.0
    moveX = 0
    moveY = 0

    img = Array{RGB{Float64}, 2}(undef,h, w)
    maxIter = 30

    for x in 1:w
        for y in 1:h
            i = maxIter
            c = Complex(
                (2*x - w) / (w * zoom) + moveX,
                (2*y - h) / (h * zoom) + moveY
            )
            z = c
            while abs(z) < 2 && (i -= 1) > 0
                z = z^2 + c
            end
            r,g,b = hsv2rgb(i / maxIter * 360, 1, i / maxIter)
            img[y,x] = RGB{Float64}(r, g, b)
        end
    end

    save("mandelbrot_set2.png", img)
end

mandelbrot()

RRRLRRLRRR

RRRLR9000000

RRLRLLRRRRLL

RRLR

RRLLLRLRL

RRLLLRLLLRLL

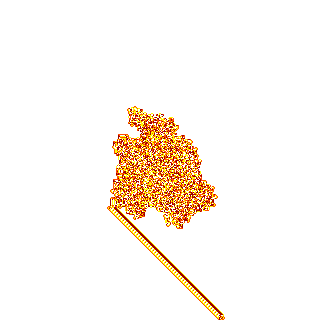
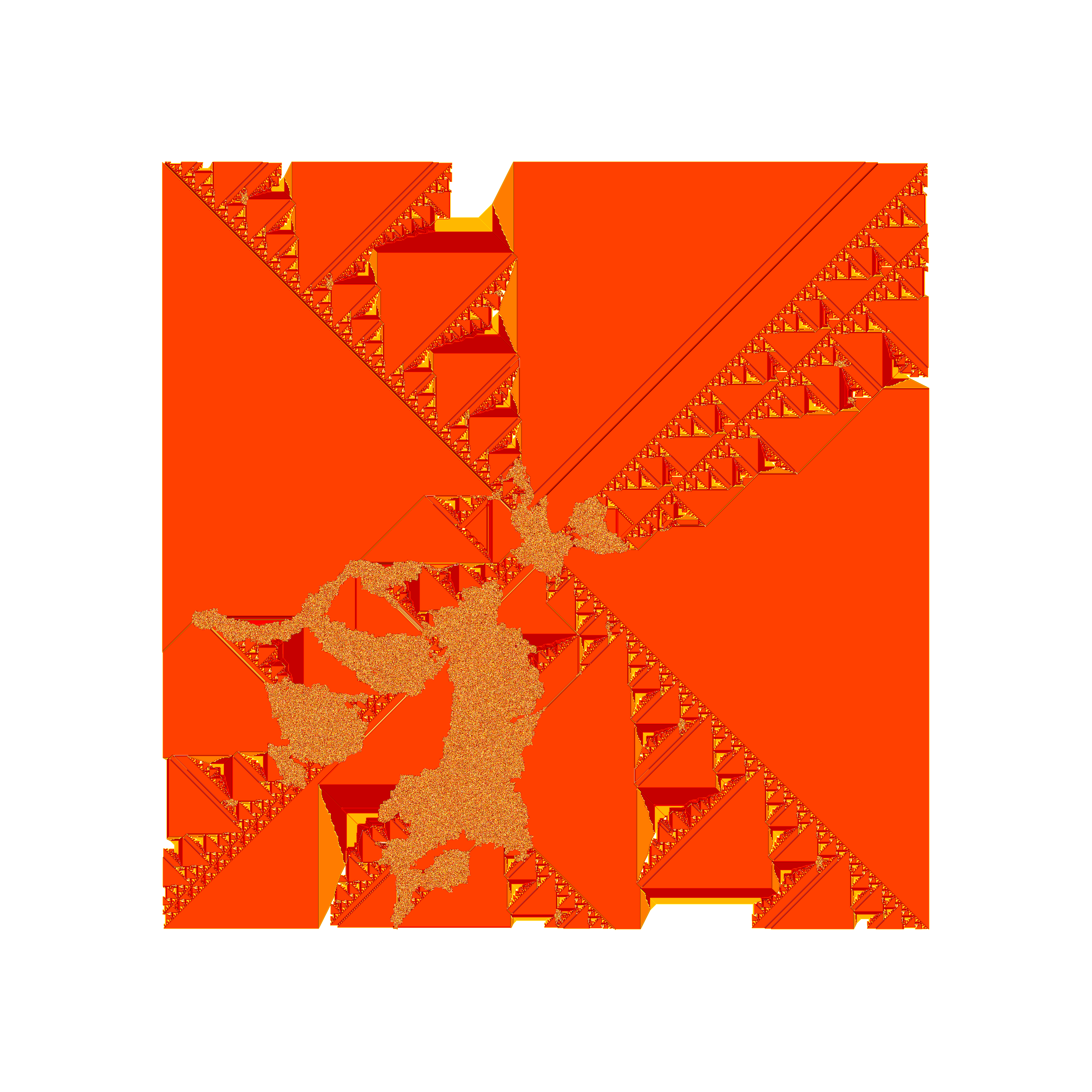
RRLLLRLLLLL_200000000

— . :

RRLLLL30_000_000_000

Rllr

RLLLLRRRLLL

RLLLLLLLRRL

LLRLLLL

, . (-), -, , , ! , !

. ,

, . ( - . )

Das Thema zellulare Automaten mit dem Wachstum der Rechenleistung und der Verbesserung von Algorithmen wird immer beliebter. Wolfram hat einen kleinen Blog-Beitrag zu diesem Thema, und jeder kann es selbst sehen - es gibt viele Artikel, die unterschiedlichsten: Sie sind mit neuronalen Netzen, Zufallszahlengeneratoren, Quantenpunkten, Komprimierung und vielem mehr befreundet ...

Und schließlich die selbstkopierende Struktur, die Ted Codd geschaffen hat , um für ein Pint Bier zu argumentieren

Julia und zellulare Automaten

More articles: