Faradaysches Gesetz oder wie ein Magnet in einem Kupferrohr steckt

Bild von der Popular Mechanics- Website .

Viele haben die Erfahrung mit einem Permanentmagneten gesehen, der in einem dickwandigen Kupferrohr stecken zu bleiben scheint. In diesem Artikel werden wir die Physik des Prozesses verstehen.
Zuerst schreiben wir die Formel des Magnetfelds des Permanentmagneten und berechnen, welcher Magnetfluss durch den Rohrquerschnitt fließt. Dann bewegen wir den Magneten und finden heraus, welcher induzierte elektrische Strom im Metall entsteht, wie hoch die Verlustleistung ist, schreiben und lösen die Bewegungsgleichung des Permanentmagneten.

Und wenn Sie bis zu diesem Ort gelesen haben und keine Angst hatten, willkommen bei kat - dann wird es interessanter!

Ich selbst habe lange darüber nachgedacht, dieses Problem gründlich zu verstehen. Und vor kurzem begann ein Gespräch mit einem Arbeitskollegen. Sein Kind wurde gebeten, in der Schule eine wissenschaftliche Demonstration durchzuführen, für die Papa ein Stück Kupferrohr und einen Neodym-Eisen-Bor-Magneten bekam. Das Kind verstand, demonstrierte die Erfahrung vor der Klasse, gab Erklärungen, aber weder die Klasse noch der Lehrer waren besonders beeindruckt. Bei einem Wettbewerb wissenschaftlicher Experimente gewann ein Vulkan (!) Aus Soda und Zitronensäure =) Mein Kollege und ich sahen uns kurz um und stellten fest, dass es klar war, dass es dunkel war. Und in der Literatur ist zu diesem Thema nicht viel geschrieben worden. Dieses Gespräch motivierte mich zu versuchen, durch den Dschungel zu kommen. In diesem Artikel schreibe ich, was ich getan habe.

Versuchsbeschreibung

Schauen wir uns zunächst ein Video an, das die Erfahrung demonstriert. Bevor wir uns mit der Theorie befassen, wird es nützlich sein, ein Bild davon zu präsentieren, was im Allgemeinen geschieht. Im Internet wurde diese Erfahrung viele Male auf Video erklärt und demonstriert. Aber ich muss es auch hier beschreiben, damit später klar wird, wovon wir abstoßen.

Der Experimentator platziert einen Permanentmagneten in Form einer kleinen Kugel in einem Kupferrohr, das er vertikal hält. Entgegen den Erwartungen fällt der Ball nicht mit einer Beschleunigung der Schwerkraft durch das Rohr, sondern bewegt sich viel langsamer im Rohr.

Erfahrungsgemäß beobachten wir also, wie sich ein Permanentmagnet mit konstanter Geschwindigkeit in einem hohlen Kupferrohr bewegt. Wir fixieren einen beliebigen Punkt im Körper des Kupferrohrs und zeichnen mental einen Querschnitt. Ein von einem Permanentmagneten erzeugter Magnetfluss fließt durch diesen Abschnitt des Kupferrohrs. Aufgrund der Tatsache, dass sich der Magnet entlang des Rohrs bewegt, ist eine VariableDer magnetische Fluss nimmt entweder zu oder ab, je nachdem, ob sich der Magnet dem Punkt nähert oder von diesem wegbewegt, an dem wir den Abschnitt mental durchgeführt haben. Nach den Maxwellschen Gleichungen erzeugt ein alternierender magnetischer Fluss im Allgemeinen ein elektrisches Wirbelfeld im gesamten Raum. Dieses elektrische Feld setzt jedoch nur dort, wo sich ein Leiter befindet, bewegungsfreie Ladungen im Leiter frei - es entsteht ein kreisförmiger elektrischer Strom, der bereits ein eigenes Magnetfeld erzeugt und mit dem Magnetfeld eines sich bewegenden Permanentmagneten interagiert. Einfach ausgedrückt erzeugt ein kreisförmiger elektrischer Strom ein Magnetfeld mit dem gleichen Vorzeichen wie ein Permanentmagnet, und eine bestimmte Verlustkraft wirkt auf den Magneten und insbesondere die Reibungskraft. Der Leser kann zu Recht eine Frage stellen:"Reibung von was über was?" Zwischen dem Magnetfeld des Dipols und dem Leiter tritt Reibung auf. Ja, diese Reibung ist nicht mechanisch. Vielmehr berühren sich die Körper nicht. Nun, lass! Es gibt immer noch Reibung!

Im Allgemeinen sieht in Worten alles mehr oder weniger komplex aus, aber kann dies in der Sprache der Mathematik beschrieben werden? Lass uns anfangen ...

Mathematische Beschreibung

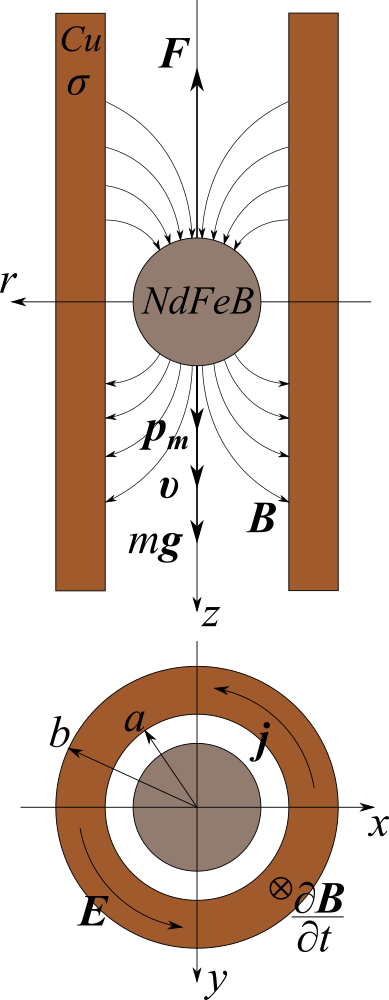Zuerst brauchen wir ein mathematisches Modell eines Permanentmagneten. Meiner Meinung nach ist es zweckmäßig, sich einen Permanentmagneten als magnetischen Dipol vorzustellen.

$$

$$\vec{B}=\frac{\mu_0}{4\pi}\left(\frac{3(\vec{p}_m\cdot\vec{r})\vec{r}}{r^5}-\frac{\vec{p}_m}{r^3}\right)$$

Die Notation wird hier akzeptiert. $$$\vec{r}=(r,z)$ Ist der Radiusvektor vom Zentrum des Dipols zum Beobachtungspunkt, $$$\vec{p}_m$Ist der Vektor des Dipolmoments.

Als nächstes müssen wir schreiben$$$z$- eine Komponente des magnetischen Induktionsvektors zur Berechnung des im Querschnitt des Metalls des Kupferrohrs erfassten Magnetflusses. Wir schreiben$$$z$-Komponente des Magnetfeldes hier

$$

$$B_z(r,z) = \frac{\mu_0\,p_m}{4\pi}\frac{2z^2 - r^2}{\left(r^2 + z^2\right)^\frac{5}{2}}$$

Nun schreiben wir den Ausdruck für den Magnetfluss durch den Bereich, der von einem Radiuskreis bedeckt ist $$$r$ auf Distanz $$$z$ vom Dipol.

$$

$$\Phi(r,z) = \int_0^{2\pi}\int_0^r B_z(r',z)\,r'\,dr'\,d\varphi = 2\pi\int_0^r \frac{\mu_0\,p_m}{4\pi}\frac{2z^2 - r'^2}{\left(r'^2 + z^2\right)^\frac{5}{2}}\,r'\,dr'$$

Sie werden es nicht glauben, aber dieses Integral wird genommen. Ich werde nicht langweilen. Die Antwort ist sehr schön

$$

$$\Phi(r,z) = \frac{\mu_0\,p_m}{2}\frac{r^2}{\left(r^2 + z^2\right)^\frac{3}{2}}$$

Aufgrund der Tatsache, dass sich der Dipol entlang der Achse bewegt $$$z$ mit Geschwindigkeit $$$v$müssen Sie auch eine Standardsuche durchführen $$$\Phi(r, z)\rightarrow \Phi(r, z - v t)$
Es scheint an der Zeit zu sein, eine der großen Gleichungen von Maxwell um Hilfe zu rufen, nämlich genau die Gleichung, die das Faradaysche Gesetz beschreibt :

Änderung des Magnetflusses durch eine offene Oberfläche $$$S$mit dem entgegengesetzten Vorzeichen genommen ist proportional zur Zirkulation des elektrischen Feldes in einem geschlossenen Kreislauf $$$L$Das ist die Grenze der Oberfläche $$$S$

$$

$$\oint_L \vec{E}\,dl = -\frac{\partial}{\partial t}\int_S \vec{B}\,d\vec{s}$$

Oder das Gleiche

$$

$$2\pi r E_\varphi = -\frac{\partial}{\partial t}\Phi(r,z - v t)$$

Hier haben wir die axiale Symmetrie des Problems in Bezug auf die Achse verwendet $$$z$und berücksichtigte auch, dass das induzierte elektrische Feld nur die azimutale Komponente aufweist $$$\vec{E} = E_\varphi \vec{e}_\varphi$.
Von hier aus kann man die azimutale Komponente des durch den Magneten induzierten elektrischen Feldes finden.

$$

$$E_\varphi(r,z) = -\frac{1}{2\pi r}\frac{\partial}{\partial t}\Phi(r, z - v t)=-\frac{3\mu_0\,p_m}{4\pi}\frac{rv(z-v t)}{\left(r^2 + (z-v t)^2\right)^\frac{5}{2}}$$

Nachdem wir einen Ausdruck für das elektrische Feld haben, können wir uns an das Rohr erinnern. Wie in der obigen Abbildung gezeigt, beträgt der Innenradius des Rohrs$$$a$und das Äußere - $$$b$. Das Rohrmaterial ist Kupfer. Im Moment brauchen wir nur die elektrische Leitfähigkeit von Kupfer. Wir bezeichnen die Leitfähigkeit mit$$$\sigma$.
Ein elektrisches Feld in einem Leiter verursacht einen elektrischen Strom. Daher können wir das Ohmsche Gesetz in Differentialform schreiben

$$

$$\vec{j} = \sigma \vec{E}$$

Elektrischer Strom verursacht wiederum ohmsche Verluste im Leiter. Mit anderen Worten, Energie wird im Leiter abgeführt und geht in Form von Wärme in unserem gesamten Volumen des Leiters in Form von Wärme über.
Die Volumenleistungsdichte von ohmschen Verlusten ist per Definition gleich

$$

$$w = \vec{j}\cdot\vec{E} = \sigma E^2$$

Wenn sich der Magnet dagegen von oben nach unten bewegt, nimmt die potentielle Energie des Magneten im Gravitationsfeld der Erde ab, die Bewegungsgeschwindigkeit bleibt jedoch konstant, dh sie wächst nicht , wie dies beim freien Fall der Fall ist. Dies bedeutet nur eines: Die potentielle Energie des Magneten wird im Leiter abgeführt. Und unter dem Gesichtspunkt der auf den Magneten einwirkenden Kräfte wirkt die Reibungskraft auf ihn, was ihn verlangsamt und die potentielle Energie des Magneten in Wärme abführt.
Wir schreiben nun die Leistungsbilanz in das Problem: Die Abnahmerate der potentiellen Energie ist gleich der Leistung der ohmschen Verluste im Leiter.

$$

$$\frac{dE_p}{dt} = P$$

$$

$$-mg\dot{z} = \int_V w\,dV$$

$$

$$mgv = \int_{-\infty}^{\infty}\int_0^{2\pi}\int_a^b \sigma E^2\,r\,dr\,d\varphi\,dz$$

Hierbei ist zu beachten, dass die potentielle Energie in den in der obigen Abbildung gezeigten Koordinaten gleich ist $$$E_p = - mgz$und um die Gesamtleistung der ohmschen Verluste zu ermitteln, ist eine Integration erforderlich $$$w$über das gesamte Volumen des Leiters. Wir betrachten die Rohrlänge als unendlich. Dies ist nicht so weit von der Wahrheit entfernt, da im Experiment aus dem Video der Durchmesser des Magneten viel kleiner als die Länge des Rohrs ist.

Das letzte dreifache Integral sieht sehr kompliziert aus. Und so ist es! Aber erstens die azimutale Integration$$$\varphi$ kann einfach durch Multiplizieren mit ersetzt werden $$$2\pi$aufgrund der axialen Symmetrie des Problems. Zweitens kann die Integrationsreihenfolge in diesem speziellen Integral geändert und zuerst überintegriert werden$$$z$und dann danach $$$r$. Drittens bei der Integration über$$$z$ Über unendliche Grenzen hinweg können wir den Begriff sicher verwerfen $$$-vt$. Das verbleibende Integral wird von der Maschine übernommen.

$$

$$\int_{-\infty}^\infty \frac{z^2\,dz}{\left(r^2 + z^2\right)^5} = \frac{5\pi}{128r^7}$$

Das Ergebnis ist eine Antwort auf die volle Leistung der ohmschen Verluste

$$

$$P = \frac{15}{1024}\,\mu_0^2\,p_m^2\,\sigma\left(\frac{1}{a^3} - \frac{1}{b^3}\right)v^2 = k\,v^2$$

Hier haben wir nach dem zweiten Gleichheitszeichen den Reibungskoeffizienten angegeben

$$

$$k = \frac{15}{1024}\,\mu_0^2\,p_m^2\,\sigma\left(\frac{1}{a^3} - \frac{1}{b^3}\right)$$

Beachten Sie, dass der Reibungskoeffizient $$$k$ hängt nur von der Magnetisierung des Magneten ab $$$p_m$, Leitermaterialeigenschaften $$$\sigma$ und geometrische Abmessungen des Rohres $$$a$ und $$$b$- das heißt, es hängt ausschließlich von den Parametern des Magneten und des Rohrs ab und hängt beispielsweise nicht von der Geschwindigkeit oder der Zeit ab. Dies ist ein gutes Zeichen für uns und ein kleiner Kredit für die gefundenen Formeln! Von hier aus wird klar, warum ein Kupferrohr zum Nachweis der Erfahrung ausgewählt wurde und nicht etwa ein Stahlrohr. Die Reibung hängt linear von der Leitfähigkeit ab$$$\sigma$und die Leitfähigkeit von Stahl ist um eine Größenordnung geringer.



Kann jetzt aufnehmen

$$

$$mgv=kv^2\\mg = kv$$

Und plötzlich (!) Ist vor uns Newtons drittes Gesetz! Die Stärke der Wirkung ist gleich der Stärke der Reaktion. Wir können die konstante Geschwindigkeit des Magneten finden

$$

$$v_s = \frac{mg}{k}$$

Bewegungsgleichung

Es war die Wende der Bewegungsgleichung. Unter Verwendung des zweiten Newtonschen Gesetzes wird es sehr einfach geschrieben

$$

$$ma=mg - kv\\ m\ddot{z} + k\dot{z} = mg$$

Löse die Gleichung für $$$z(t)$uninteressant, denn nur die Koordinate ändert sich mit konstanter Geschwindigkeit. Es ist viel nützlicher zu wissen, wie schnell sich der Fall stabilisiert, was der stationären Fallrate entspricht. Im Allgemeinen müssen Sie diese Gleichung für die Geschwindigkeit lösen

$$

$$\dot{v} + \frac{k}{m} v = g$$

Und die Lösung wird sein

$$

$$v(t) = v_0\,e^{-\alpha t} + v_s\left(1 - e^{-\alpha t}\right)$$

Hier $$$\alpha = k/m$- Dämpfungskoeffizient. Die charakteristische Zeit, um den stationären Fallmodus zu erreichen, ist$$$\tau = \alpha^{-1}$. Startgeschwindigkeit -$$$v_0$, konstante Geschwindigkeit - $$$v_s$.

Im Allgemeinen ist dies die Gleichung eines Fallschirmspringers. Dies ist wahrscheinlich der Grund, warum der Artikel von Popular Mechanics "Magnetic Parachute" heißt.

Numerisches Experiment

Und jetzt wird es etwas geben, für das all dies konzipiert wurde. Sie haben eine Theorie hierher gebracht, wissen Sie. Was kann sie? Plötzlich ist es wie ein Schatten auf dem Weidezaun? Oder es funktioniert überhaupt nicht ...

Zuerst müssen Sie sich mit der Geometrie des Problems befassen. Das Video vom MIT ist daher amerikanisch. Ich werde versuchen, die Größe ihrer Demo-Installation in Zoll zu erraten (sie messen auch gerne alles in Zoll). Die Größe des Magneten ist ähnlich wie$$$d = 1/2$Zoll im Durchmesser. Dies ist einer von denen, die zum Verkauf stehen. Dann beträgt die Masse eines solchen Magneten ungefähr$$$m = 8$ d. Die Länge des Kupferrohrs ist ähnlich wie $$$l = 12$ Zoll (1 Fuß) und der Innen- und Außendurchmesser des Rohrs sind am wahrscheinlichsten $$$2a = 3/4$ Zoll $$$2b = 3/2$Zoll.

Mit Geometrie irgendwie aussortiert. Nun physikalische Eigenschaften. Kupferleitfähigkeit$$$59.5\times 10^6$S / m

Früher wurde hier geschrieben, dass ich die Restmagnetisierung eines Neodym-Magneten nicht mit seinem äquivalenten magnetischen Moment verknüpfen konnte. Aber es gab gute Leute in den Kommentaren. BenutzerDenishwDie vorgeschlagene Quelle (siehe Absatz 5 in der Referenzliste), in der Sie lesen können, half bei der Durchführung der erforderlichen Berechnungen und überprüfte sie sogar im FEMM-Simulator.


Berechnung des Magnetfeldes einer Kugel aus NdFeB auf dem FEMM-Simulator. Bild vom Benutzer bereitgestelltDenishw

Also, was wurde herausgefunden. Der NdFeB-Magnet gehört zur Klasse der Paramagnete, da unter dem Einfluss eines externen Feldes das interne Feld verstärkt wird. Darüber hinaus kann die NdFeB-Legierung das interne Feld nach Beendigung des externen Feldes aufrechterhalten. Diese Tatsache klassifiziert NdFeB als Ferromagneten. Wenn wir die Induktion des inneren Feldes eines Magneten mit bezeichnen$$$B$und das externe Magnetfeld $$$H$dann Gleichheit

$$

$$B = \mu \mu_0 H = (1 + \chi)\mu_0 H = \mu_0(H + I)$$

Hier $$$\chi$ - die magnetische Suszeptibilität des Stoffes und $$$I$Ist der Magnetisierungsvektor der Substanz.

Wenn ein Magnet in einer Fabrik hergestellt wird, wird er durch ein externes Feld magnetisiert.$$$H$und dann wird das externe Feld ausgeschaltet und der Magnet behält eine gewisse Restmagnetisierung bei $$$B_r$. Es ist bekannt, dass für Neodym-Magnete die remanente Magnetisierung ungefähr ist$$$B_r = 1\,..\,1.3$ T. Nun, wenn Sie das externe Feld ausschließen $$$H$ aus der vorherigen Gleichung erhalten wir

$$

$$B_r = \mu_0I$$

Wo finden wir das magnetische Moment pro Volumeneinheit des Materials? $$$I$ wie

$$

$$I = \frac{B_r}{\mu_0}$$

Um das magnetische Moment des Magneten als Ganzes zu finden, müssen Sie multiplizieren $$$I$ pro Ballvolumen $$$V$

$$

$$p_m=IV=I\cdot\frac{4}{3}\pi\left(\frac{d}{2}\right)^3$$

Zur Restmagnetisierung $$$B_r = 1$ T wird erhalten $$$p_m = 0.853$Am².
Unten ist eine Grafik$$$z$- Komponenten des Magnetfeldes in Abhängigkeit von der Radialkoordinate in unserem Problem in einem Abstand von der Hälfte des Durchmessers der Kugel.


$$$z$-Komponente eines Magnetfeldes nahe der Oberfläche eines Permanentmagneten

Sobald es möglich war, mit einem Gerät zu messen. Felder direkt auf der Oberfläche solcher Magnete sind normalerweise geringer als die Restmagnetisierung und betragen etwa mehrere tausend Gauß. Was ich für einen rechteckigen Magneten gemessen habe, waren ungefähr 4.500 Gs. Daher haben wir ein sehr realistisches Ergebnis auf dem Magnetfelddiagramm.

Nun werden wir die Lösung der Bewegungsgleichung verwenden, um die Geschwindigkeit des Magneten zu zeichnen. Für alle oben ausgewählten Parameter ist der Reibungskoeffizient gleich$$$k = 1.015$ N / (m / s), konstante Geschwindigkeit - $$$v_s = 7.77$cm / s - nur etwa 3 Zoll pro Sekunde! Im Video passiert der Ball in ca. 4 Sekunden ein 12-Zoll-Rohr.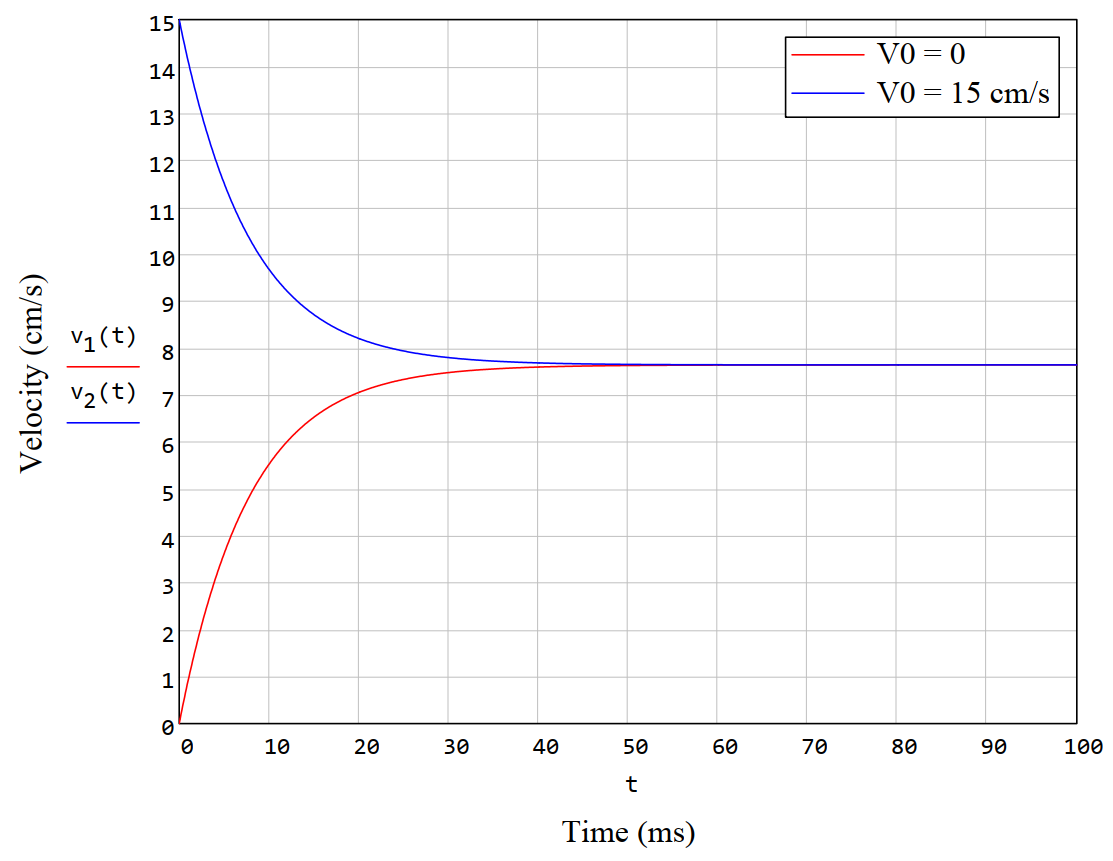


Diagramm zur Lösung der Bewegungsgleichung eines Magneten in einem Kupferrohr


Und wir machen weiter. Die Verlustleistung beträgt ungefähr$$$P \approx 6$ mW und die charakteristische Zeit zum Erreichen des stationären Zustands ist $$$\tau \approx 8$Frau Unten sind die Grafiken.$$$v(t)$ für zwei verschiedene Anfangsgeschwindigkeiten: Null und $$$v_0 = 15$cm / s.

Und dazu der Benutzervashu1Zu Recht bemerkt, dass es schön wäre, den in einem Kupferrohr induzierten Strom zu kennen. Nun, und es ist möglich. Integrieren

$$

$$J = \int_{0}^{\infty}\int_a^b \sigma E(r,z)\,dr\, dz = \frac{\sigma\, v\,\mu_0\, p_m}{4\pi}\left(\frac{1}{a} - \frac{1}{b}\right)$$

Integrieren durch $$$z$es ist nach semi-infiniten Grenzen notwendig, da in der anderen Rohrhälfte der Strom in die entgegengesetzte Richtung fließt. Ich habe die Antwort bekommen$$$J = 20$A. Ehrlich gesagt hatte ich nicht erwartet, eine so große Strömung zu bekommen. Beim Benutzervashu1es stellte sich heraus, 50 A, was anscheinend auch nicht weit von der Realität entfernt ist. Ich glaubevashu1Ich habe die Summe der Ströme in der gesamten Leitung berechnet, was aus Leistungsgründen auch sinnvoll ist.

Hier ist eine solche Studie. Hoffe das war interessant. Hinterlassen Sie Ihre Kommentare. Ich werde versuchen, allen zu antworten. Wenn Ihnen der Artikel gefallen hat, unterstützen Sie den Autor wie oder plus in Karma. Danke fürs Lesen.

Literatur

1. Jackson, J. Klassische Elektrodynamik: Per. aus dem Englischen Welt, 1965.
2. Landau, L. D. & Lifshitz, E. M. (1941). Feldtheorie. Moskau; Leningrad: Staatlicher Verlag für technische und theoretische Literatur.
3. Sivukhin, D. V. „Allgemeiner Kurs der Physik. Band 3. Strom. " Moskau, Verlag "Science", die Hauptausgabe der physikalischen und mathematischen Literatur (1977).
4. Yavorsky, B. M. und A. A. Detlaf. "Handbuch der Physik." (1990).
5. Kirichenko N.A. Elektrizität und Magnetismus. Lernprogramm. - M.: MIPT, 2011 .-- 420 p.