Ein übermäßiger Wunsch nach Genauigkeit übte einen Effekt aus, der die Kontrolltheorie und die Systemtheorie negiert, da dies dazu führt, dass sich die Forschung in diesem Bereich auf diejenigen und nur jene Probleme konzentriert, die präzise gelöst werden können. Viele Klassen wichtiger Probleme, bei denen Daten, Ziele und Einschränkungen zu komplex oder schlecht definiert sind, um eine genaue mathematische Analyse zu ermöglichen, sind geblieben und bleiben nur deshalb am Rande, weil sie nicht mathematisch interpretiert werden können. L. Zade
Definition und Eigenschaften
In der Welt ist vieles nicht nur in Weiß und Schwarz, in Wahrheit und Wahrheit unterteilt ... Eine Person verwendet viele unscharfe Konzepte, um physikalische Größen, Zustände von Objekten und Systemen auf einer ungefähren qualitativen Ebene zu bewerten und zu vergleichen. So kann jeder von uns die Temperatur außerhalb des Fensters schätzen, ohne auf ein Thermometer zurückgreifen zu müssen, und sich nur an seinen eigenen Gefühlen und einer Skala von ungefähren Schätzungen orientieren („bewölkt genug, um einen Regenschirm mitzunehmen“).
Eine qualitative Bewertung besitzt jedoch nicht die Additivitätseigenschaft, die unseren üblichen Zahlen innewohnt. Das heißt, wir können das Ergebnis von Operationen nicht für ungefähre Schätzungen („kleiner Geldbetrag“ + „kleiner Geldbetrag“) bestimmen, im Gegensatz zu beispielsweise natürlichen Zahlen (2 + 2). Wir können nicht feststellen, da eine qualitative Bewertung stark vom Entscheidungsträger, dem Kontext und der Bedeutung abhängt, die in einem bestimmten Fall investiert wurden.
Auf der Welt gibt es jedoch genügend Mengen, die wir aus dem einen oder anderen Grund nicht genau einschätzen können: den Ordnungsgrad im Raum, das "Prestige" des Autos, die Schönheit eines Menschen, die "Ähnlichkeit" der Dinge ... Aber ich möchte mit ihnen wie mit den üblichen Zahlen arbeiten würde für Automatisierungsaufgaben.
. 1964 .
.
( )  () U
() U )%20) ,
,  ,
,
%20) —
—  ,
, ![\ mu_A (u): U → [0; 1]](https://tex.s2cms.ru/svg/%20%5Cmu_A%20(u)%3AU%20%E2%86%92%5B0%3B1%5D%20) .
. %7D(%5Cmu_A%20(u)%20%2F%20u)%20%3D%20%5Cleft%5C%7B%20%20(%5Cmu_A(u)%20%2F%20u)%20%5Cright%5C%7D%20%20) .
.
U %20) ( ) u (-)
( ) u (-)  . , . - .
. , . - .
%20) ( . ), – . – U
( . ), – . – U  . , , .
. , , .
, %20%3D%20%5Cbegin%7Bcases%7D1%20%26%20u%20%5Csubseteq%20A%20%5C%5C0%20%26%20u%20%5Cnsubseteq%20A%20%5Cend%7Bcases%7D%20) , .
, .
, %20) :
:
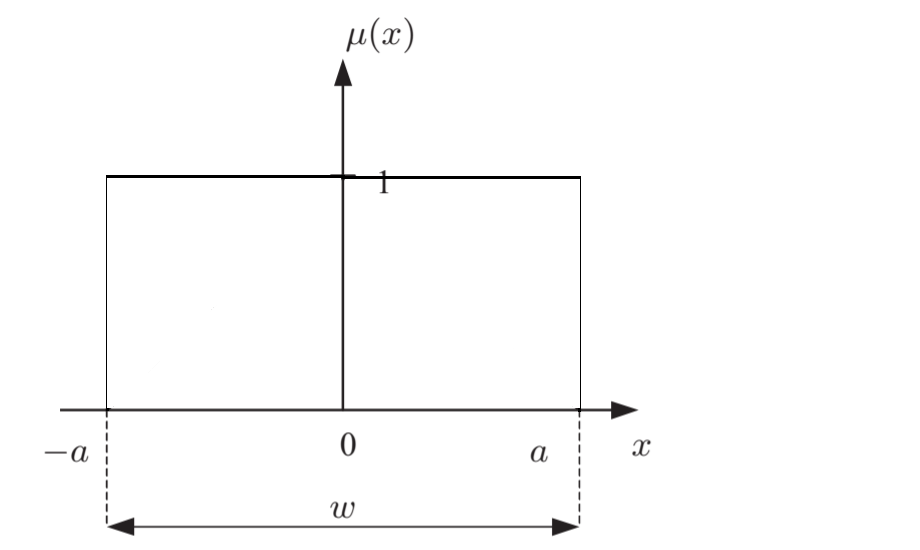
-a≤x≤a.
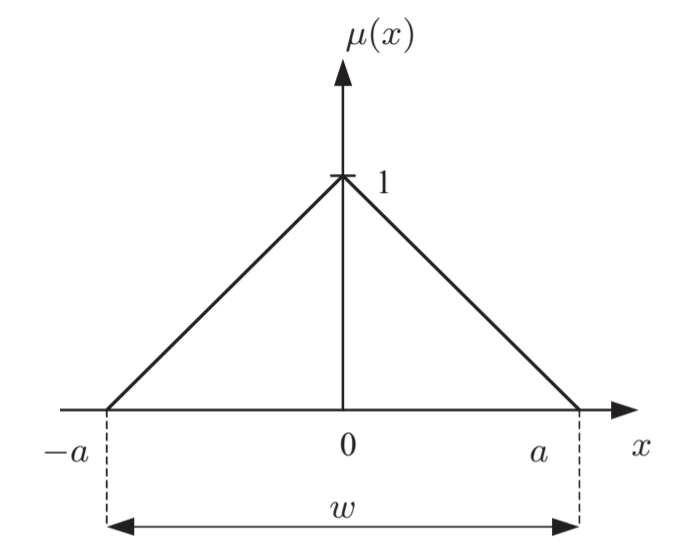
“ ”.
%3D%20%5Cfrac%7B(a-%7Cx%7C)%7D%7Ba%7D%2C%20%20-a%20%5Cleq%20x%20%5Cleq%20a%20)
 .
.
.
– , 1. 0.
, %20) 0.5, . -a/2 a/2.
0.5, . -a/2 a/2.
)%2Cu%20%5Csubseteq%20U%20) .
.
, 1, . – .
, , 0, .
, 1 .
2 %20)
%3E0%2C%20%20x%20%5Csubseteq%20X%20%5Cright%5C%7D%20) –
–  .
. 
 .
.
, x, %3D0%20) ; –
; – %7D%3D0%20) .
.
, , . :
- , ;
- , ;
- , , .
:  — U,
— U,  . , .
. , .
 ,
, %3D%20%5Cmu_B(x)%20) .
.
 ,
, %20%5Cleq%20%0A%20%5Cmu_B%20(x)%20) x.
x.
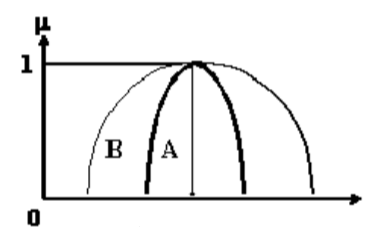
 ,
, %20%3D%20max%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20) . ,
. , %20%3D%20%5Cmu_A(x)%20%5Cvee%20%5Cmu_B%20(x)%20) . (t– s–)
. (t– s–)
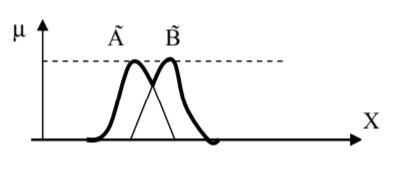
 ,
, %20%3D%20min%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20) . ,
. , %20%3D%20%5Cmu_A(x)%20%5Cwedge%20%5Cmu_B%20(x)%20) . (t-)
. (t-)
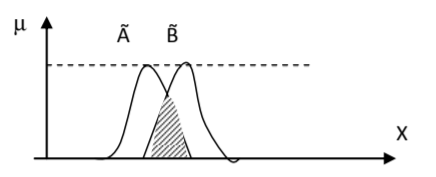
:
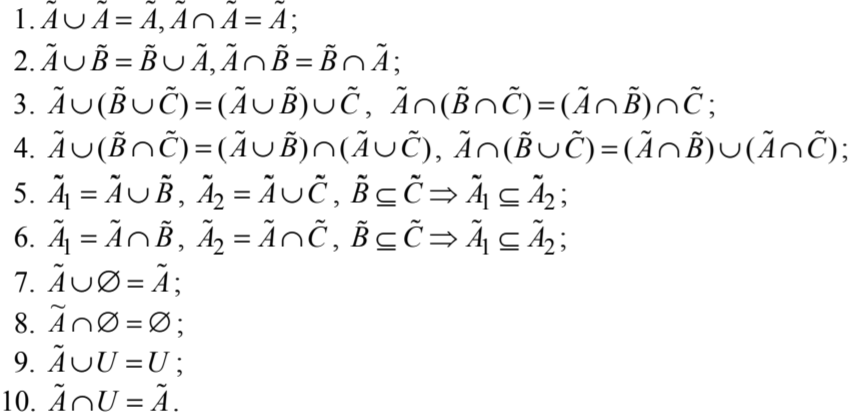
. , , . , min max .
 ,
, %20%3D%20%5Cmu_A(x)%20-%20%5Cmu_%7BA%20%5Ccap%20B%7D(x)%20%3D%20%5Cmu_A(x)%20-%20min%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20%3D%20max(0%3B%20%5Cmu_A(x)%20-%20%5Cmu_B(x))%20) .
.

 . ,
. , %20%3D%201-%20%5Cmu_%7B%5Coverline%7BA%7D%7D(x)%20) .
.
. , , , (,  ). :
). :
α- . α-  ,
, %20%5Cgeq%20%5Calpha%20) .
.
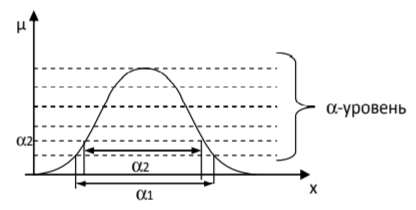
.  , M — .
, M — .
 ,
, %3D%20%5Cmu_A%5E%7B%5Cbeta%7D(x)%20) . :
. :
- β = 2 ( CON(A) ). , . , “ ” ;
- β = 0.5 ( DIL(A) ). , . “ ”.
.
%20%3D%20%5Cmu_A(x)%20*%20%5Cmu_B%20(x)%20) .
.
%20%3D%20(%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%201)%20%5Cvee%200%20) .
.
%20%3D%20%5Cbegin%7Bcases%7D%5Cmu_B(x)%20%26%20%5Cmu_A(x)%20%3D%201%5C%5C%5Cmu_A(x)%20%26%20%5Cmu_B(x)%20%3D%201%5C%5C0%20%26%20%5Cend%7Bcases%7D%20) .
.
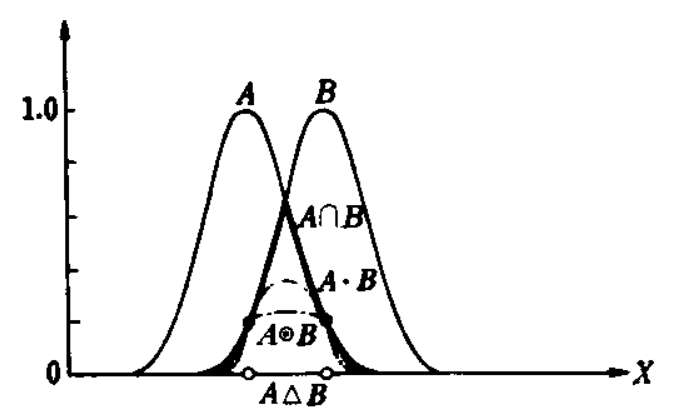
%20%3D%20%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%20%5Cmu_A(x)*%5Cmu_B(x)) .
.
%20%3D%20(%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%201)%20%5Cwedge%201%20) .
.
%20%3D%20%5Cbegin%7Bcases%7D%5Cmu_B(x)%20%26%20%5Cmu_A(x)%20%3D%200%5C%5C%5Cmu_A(x)%20%26%20%5Cmu_B(x)%20%3D%200%5C%5C1%20%26%20%5Cend%7Bcases%7D%20) .
.
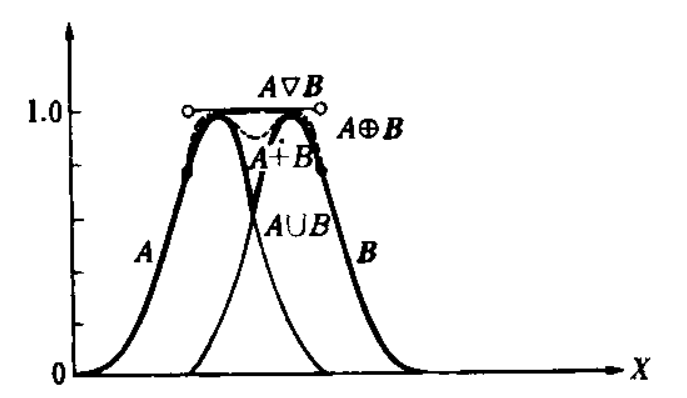
- – A B λ (1 — λ) ( A B). %20%3D%20%5Clambda%20*%20%5Cmu_A(x)%20%2B%20(1%20-%20%5Clambda)%20*%20%5Cmu_B(x)%20) .
.
, λ- :

?
, , . . , ( , ). 2 – .
, . , , , . : , .
, , . , .
, , , , , :
- 0 <= μ(x) <= 1;
- ( );
- Die Funktion und die Menge der definierten Funktionen müssen eine natürliche Differenzierung der Konzepte aufweisen, die durch benachbarte Mengen dargestellt werden.
- Es sollte keine Lücken in der universellen (oder zur Berücksichtigung begrenzten) Menge geben, für die keine Menge zugeordnet ist.
- Für benachbarte Mengen muss das Maximum von einem mit dem Minimum des anderen übereinstimmen, und der Schnittpunkt ihrer Graphen muss den Übergangspunkten entsprechen;
- und einige andere aufgabenspezifische.
Es gibt jedoch Ausnahmesituationen, in denen eine Funktion anhand des Kontexts bestimmt werden muss. Der Aufbau solcher Funktionen ist ein eigenständiges und recht kompliziertes Thema.
Und das ist alles für heute.