Arbitrage-Handel (Bellman-Ford-Algorithmus)

Der Handel an der Börse ist normalerweise mit Risiken verbunden. Dies gilt absolut für die meisten Handelsstrategien. Der Erfolg des Handels in diesen Fällen hängt ausschließlich von der Fähigkeit ab, Risiken richtig einzuschätzen und zu managen. Aber nicht alle Handelsstrategien sind. Es gibt risikofreie Strategien, zu denen insbesondere die Schiedsgerichtsbarkeit gehört. In diesem Artikel wird erläutert, was Arbitrierung ist und wie sie mithilfe eines klassischen Graph-Algorithmus wie dem Bellman-Ford-Algorithmus implementiert wird.

Was ist ein Schiedsverfahren?

Bei der Schiedsgerichtsbarkeit handelt es sich um einige logisch zusammenhängende Transaktionen, die darauf abzielen, von den Preisunterschieden für dasselbe oder verwandte Vermögenswerte zur gleichen Zeit auf verschiedenen Märkten (räumliche Schiedsgerichtsbarkeit) oder auf demselben Markt zu verschiedenen Zeitpunkten (vorübergehende Schiedsgerichtsbarkeit) zu profitieren. .

Betrachten Sie als einfaches Beispiel die räumliche Arbitrage. In New York und London können Geschäfte abgeschlossen werden, um Dollar für Euro und Euro für Dollar zu kaufen. In New York kann dies zum Preis von 4 Dollar für 3 Euro und in London zum Preis von 5 Dollar für 3 Euro erfolgen. Dieser Ratenunterschied eröffnet die Möglichkeit einer räumlichen Arbitrierung.



Mit 4 Dollar kann man in New York 3 Euro kaufen. Danach kaufen Sie in London für diese 3 Euro 5 Dollar. Wie Sie sehen können, bringt eine so einfache Abfolge von Transaktionen 1 Dollar Gewinn pro 4 investierten Dollar. Wenn es anfänglich 4 Millionen US-Dollar gibt, liegt der Gewinn bereits bei einer Million.

Wenn sich die Wechselkurse (wir berücksichtigen den Spread nicht) für dasselbe Währungspaar unterscheiden, ist die zur Implementierung der Arbitrage-Strategie erforderliche Abfolge von Transaktionen sehr einfach. Wenn der Wechselkurs für ein Währungspaar festgelegt ist, jedoch mehrere Währungspaare parallel gehandelt werden, ist auch eine Schiedsgerichtsbarkeit möglich, die Reihenfolge der Transaktionen ist jedoch bereits nicht trivial. Zum Beispiel können Sie 4 Euro für 5 Dollar, 3 Pfund für 4 Euro und dann 6 Dollar für 3 Pfund kaufen. Der Gewinn aus einer solchen Abfolge von Transaktionen beträgt 1 US-Dollar pro 5 investierten US-Dollar.



Hunderte von Währungspaaren können an der Börse gehandelt werden, und die Wechselkurse ändern sich ständig. Es ist bereits unmöglich zu verstehen, welche Abfolge von Transaktionen ohne eine algorithmische Lösung Gewinn bringt.

Übergang zum algorithmischen Problem

Stellen Sie sich mögliche Devisentransaktionen in algorithmischer Form vor, und zwar in Form eines Diagramms. Die Eckpunkte in diesem Diagramm stellen Währungen dar, und die Kanten sind potenzielle Trades. Die Länge der Rippe entspricht dem Wechselkurs, zu dem die Transaktion abgeschlossen werden kann.


Die nächste Frage ist, wie man eine Abfolge von Transaktionen in einer solchen Spalte findet, die Gewinn bringt. Da es sich am Anfang der Sequenz und am Ende um dieselbe Währung handeln muss, muss die Sequenz natürlich dem Zyklus in der angegebenen Grafik entsprechen. Als nächstes müssen Sie bestimmen, wie der Wechselkurs zwischen den beiden Währungen berechnet wird, wenn sie nicht direkt, sondern über eine bestimmte dritte Währung (oder eine beliebige Anzahl von Zwischenoperationen) ausgetauscht werden. Alles hier ist auch ganz einfach. Ein solcher Wechselkurs wird als Produkt der Wechselkurse von Zwischengeschäften berechnet. Eine profitable Abfolge von Transaktionen wird, wenn dieses Produkt einen Wert von weniger als eins annimmt. Mit anderen Worten, wenn eine Währungseinheit weniger als eine Einheit derselben Währung gekauft werden kann.


Klassische Graph-Algorithmen eignen sich schlecht für die Arbeit mit Produkten mit Kantenlängen. Solche Algorithmen zielen hauptsächlich darauf ab, einen Pfad zu finden, der als Summe dieser Längen definiert ist. Um diese Einschränkung zu umgehen, gibt es jedoch einen mathematischen Weg, um von einem Produkt zu einer Summe zu gelangen. Dieser Weg ist Logarithmus. Wenn das Produkt unter dem Logarithmus erscheint, kann ein solcher Logarithmus in die Summe der Logarithmen umgewandelt werden. Auf der rechten Seite dieser Gleichung ist die gewünschte Zahl kleiner als eins, was bedeutet, dass der Logarithmus dieser Zahl kleiner als Null sein sollte.




Mit einem solchen einfachen mathematischen Trick können Sie von der Suche nach einem Zyklus, dessen Produkt aus Kantenlängen kleiner als eins ist, zur Suche nach einem Zyklus übergehen, dessen Summe der Kantenlängen kleiner als Null ist. Eine solche Aufgabe scheint bereits mit klassischen Graph-Algorithmen und genauer mit dem Bellman-Ford-Algorithmus lösbarer zu sein.

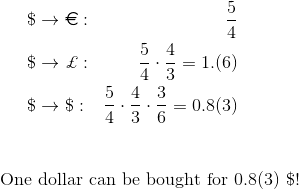
Bellman - Ford Algorithmus

Der Bellman-Ford- Algorithmus wird normalerweise verwendet, um den Abstand von einem bestimmten Scheitelpunkt zu allen anderen Scheitelpunkten eines Graphen zu ermitteln. Seine Modifikation ermöglicht jedoch das Auffinden von Zyklen negativer Länge.

Die Grundoperation dieses Algorithmus ist die Kantenrelaxation . Das Wesentliche dieser Operation ist wie folgt. Angenommen, es gibt eine Kante$$$a \rightarrow b$und auch die zuvor berechneten vorläufigen Werte der Abstände zu den Peaks sind bekannt $$$a$und $$$b$. Um eine Kantenrelaxation durchzuführen, muss der Abstand zur Spitze berechnet werden$$$b$wenn der Weg durch die Spitze ging $$$a$und Rippe $$$a \rightarrow b$. Diese Entfernung wird als Summe der Entfernung nach oben berechnet.$$$a$ und Rippenlängen $$$a \rightarrow b$. Wenn dieser Abstand geringer ist als der aktuelle vorläufige Abstand zu$$$a$dann ist dies genau die Entfernung zu $$$a$Entspricht und nimmt einen neuen, gerade berechneten Wert an.

Der Rest des Algorithmus ist ebenfalls unkompliziert. Notwendig$$$N$ Zeiten ($$$N$Ist die Anzahl der Eckpunkte des Diagramms), umgehen Sie die Liste der Kanten und wenden Sie für jede Runde eine Relaxationsoperation an. Die Komplexität des Algorithmus wird erhalten$$$N*M$ (Wo $$$N$- die Anzahl der Eckpunkte und $$$M$- Anzahl der Rippen). Bei einem Diagramm ohne negative Zyklen führt eine weitere Kantenrelaxation nicht zu einer Änderung des Abstands zu den Scheitelpunkten. Gleichzeitig verringert die Relaxation bei einem Diagramm mit einem negativen Zyklus den Abstand zu den Eckpunkten und danach$$$N$Umleitungen. Diese Eigenschaft kann verwendet werden, um den gewünschten Zyklus zu finden.

Die folgende kleine Implementierung des oben auf Kotlin beschriebenen Algorithmus soll denjenigen helfen, die mit dem Aussortieren von Code besser vertraut sind.

fun findNegativeCycle(nodes: Int, edges: Array<Edge>, source: Int): List<Int>? {
    // Initialize distances and prev arrays. All distances but the distance to
    // the source node are infinite, distance to the source node is zero.
    val distances = DoubleArray(nodes) { if (it == source) 0.0 else INFINITY }
    val prev = IntArray(nodes) { -1 }

    // Relax all edges N times where N is the number of nodes.
    repeat(nodes) {
        edges.forEach { it.relax(distances, prev) }
    }

    // Try to relax at least one more edge. If it's possible memorize the node,
    // otherwise return from the method.
    val firstRelaxedEdge = edges.firstOrNull { it.relax(distances, prev) }
    var node = firstRelaxedEdge?.to ?: return null

    // Step back N times where N is the number of nodes. As a result, the node will
    // be in the loop for sure.
    repeat(nodes) {
        node = prev[node]
    }

    // Recover the loop by the node that is inside it and prev links.
    val lastNode = node
    return buildList {
        do {
            add(node)
            node = prev[node]
        } while (node != lastNode)

        reverse()
    }
}

// Edge DTO with implemented relaxation operation.
data class Edge(val from: Int, val to: Int, val length: Double) {

    fun relax(distances: DoubleArray, prev: IntArray): Boolean {
        if (distances[from] + length >= distances[to]) {
            return false
        }

        distances[to] = distances[from] + length
        prev[to] = from
        return true
    }
}

Betrachten wir ein Beispiel mit einem kleinen Graphen, der einen Zyklus negativer Länge enthält. Damit der Algorithmus funktioniert, muss jeder Scheitelpunkt den aktuell bekannten Abstand zu ihm sowie eine Verknüpfung zu seinem vorherigen Scheitelpunkt beibehalten. Die Bezugnahme auf den vorherigen Scheitelpunkt wird in diesem Fall durch die erfolgreiche Relaxation der Rippe bestimmt. Wenn die Relaxationsoperation erfolgreich war und der Abstand zum Scheitelpunkt aktualisiert wurde, wird auch die Verknüpfung zum vorherigen Scheitelpunkt dieses Scheitelpunkts aktualisiert und nimmt den Wert des Quellscheitelpunkts der angegebenen Kante an.

Zuerst müssen Sie die Scheitelpunkte initialisieren, indem Sie den Abstand zu allen Scheitelpunkten mit Ausnahme der anfänglichen gleichen Unendlichkeit festlegen. Für den anfänglichen Scheitelpunkt wird ein Abstand von Null eingestellt.


Die erste Runde aller Rippen folgt und ihre Entspannung wird durchgeführt. Fast alle Entspannungen führen zu keinem Ergebnis, außer Rippenentspannung$$$a \rightarrow b$. Durch die Entspannung dieser Rippe können Sie den Abstand zu aktualisieren$$$b$.


Darauf folgt die zweite Runde aller Kanten des Graphen und die entsprechende Relaxation. Diesmal ist das Ergebnis eine Entspannung der Rippen.$$$b \rightarrow c$, und auch $$$b \rightarrow d$. Die Abstände zu den Gipfeln werden aktualisiert.$$$c$ und $$$d$. Hierbei ist zu beachten, dass das Ergebnis von der Reihenfolge abhängt, in der die Kanten durchlaufen werden.


In der dritten Rippenrunde ist es möglich, bereits drei Rippen, nämlich die Rippen, erfolgreich zu entspannen $$$\rightarrow d$, $$$d \rightarrow e$, $$$d \rightarrow b$. In diesem Fall, wenn die Rippen entspannt sind$$$\rightarrow d$ und $$$d \rightarrow b$bereits aufgezeichnete Entfernungen zu $$$d$und $$$b$sowie entsprechende Links zu vorherigen Eckpunkten.


In der vierten Runde werden die Rippenrelaxationsoperationen erfolgreich abgeschlossen. $$$b \rightarrow c$und $$$b \rightarrow a$. In diesem Fall werden bereits aufgezeichnete Werte der Abstände zu den Peaks erneut aktualisiert.$$$a$ und $$$c$sowie die entsprechenden Links zu vorherigen Eckpunkten.


Die fünfte Runde ist die letzte. Während dieses Spaziergangs entspannen sich die Rippen$$$\rightarrow d$, $$$d \rightarrow b$, $$$d \rightarrow e$. Hier können Sie sehen, dass das Vorhandensein eines Zyklus negativer Länge bereits bestimmte Anpassungen an den Werten der Abstände zu den Spitzen vornimmt.


Wenn der Graph nach dieser Tour keinen Zyklus negativer Länge enthalten würde, wäre der Algorithmus abgeschlossen, da die Relaxation einer Kante keine Änderungen vorgenommen hätte. Für diesen Graphen kann man jedoch aufgrund des Vorhandenseins eines Zyklus negativer Länge immer noch eine Kante finden, deren Relaxation den Abstand zu einem der Eckpunkte aktualisiert.


Es wird eine Kante gefunden, deren Entspannung die Entfernung zum Gipfel aktualisiert. Dies bestätigt das Vorhandensein eines Zyklus negativer Länge. Jetzt müssen Sie diesen Zyklus selbst finden. Es ist wichtig, dass der Scheitelpunkt, dessen Abstand jetzt aktualisiert wird, sowohl innerhalb als auch außerhalb des Zyklus liegen kann. Im Beispiel ist dies die Spitze$$$e$und sie ist aus dem Kreislauf. Als nächstes müssen Sie auf die Links zu den vorherigen Scheitelpunkten verweisen, die in allen Schritten des Algorithmus sorgfältig aktualisiert wurden. Um garantiert in den Zyklus zu kommen, müssen Sie zurücktreten$$$N$Peaks über diese Links.

In diesem Beispiel lauten die Übergänge wie folgt:$$$e \rightarrow d \rightarrow c \rightarrow b \rightarrow d \rightarrow c$. So befindet sich die Spitze$$$c$, die garantiert in einem Zyklus negativer Länge liegt.


Weiter eine Frage der Technologie. Um den gewünschten Zyklus zurückzugeben, müssen Sie die Verknüpfungen zu den vorherigen Scheitelpunkten erneut durchlaufen, bis sich der Scheitelpunkt wieder trifft$$$c$. Dies bedeutet, dass der Zyklus geschlossen wurde. Sie müssen lediglich die Reihenfolge umkehren, da die Iteration während der Iterationen über Verknüpfungen zu vorherigen Scheitelpunkten umgekehrt wurde.

Der obige Algorithmus setzt das Vorhandensein eines anfänglichen Scheitelpunkts voraus, aus dem die Abstände berechnet werden. Das Vorhandensein eines solchen Scheitelpunkts ist nicht erforderlich, damit der Algorithmus funktioniert, wurde jedoch in größerem Umfang eingeführt, um dem ursprünglichen Bellman-Ford-Algorithmus zu entsprechen. Wenn das interessierende Thema ein Zyklus negativer Länge ist, können wir annehmen, dass alle Eckpunkte eines gegebenen Graphen initial sind. Mit anderen Worten, dass der Abstand zu allen Eckpunkten anfänglich Null ist.

Fazit

Die Verwendung des Bellman-Ford-Algorithmus im Arbitrage-Handelsproblem ist ein hervorragendes Beispiel dafür, wie klassische Algorithmen echte Geschäftsprobleme insbesondere im Finanzbereich lösen können. Asymptotische Komplexität des Algorithmus, gleich$$$N^3$Für ein vollständig verbundenes Diagramm kann es sich als ziemlich groß herausstellen. Daran muss man sich wirklich erinnern. In vielen Fällen, wie zum Beispiel beim Geldwechsel, verursacht diese Komplexität jedoch aufgrund der relativ geringen Anzahl von Knoten in der Grafik keine Probleme .