🙏🏾 ✒️ ⚱️ Visualisierung von Spannungslinien und Bewegungen elektrostatischer Ladungen, Simulation der Planetenbewegung des Sonnensystems 🙇🏼 👨‍❤️‍👨 ♎️

Hallo, heute möchte ich Ihnen eine visuelle Hilfe zum Modellieren einiger physikalischer Prozesse anbieten und zeigen, wie Sie schöne Bilder und Animationen erhalten. Achtung viele Bilder.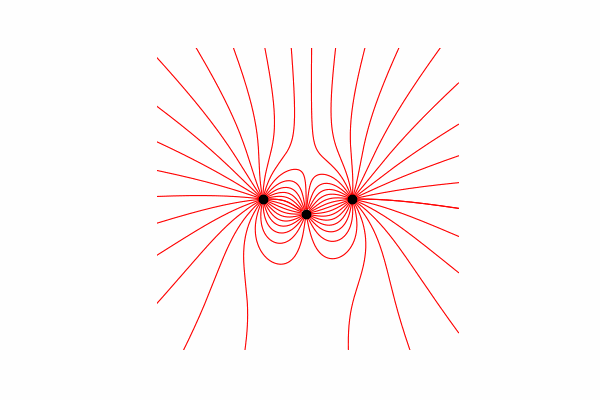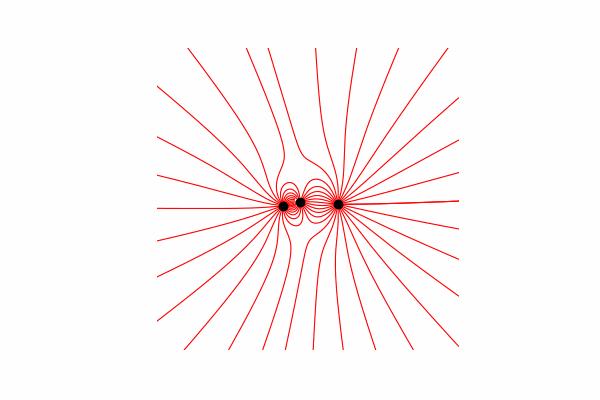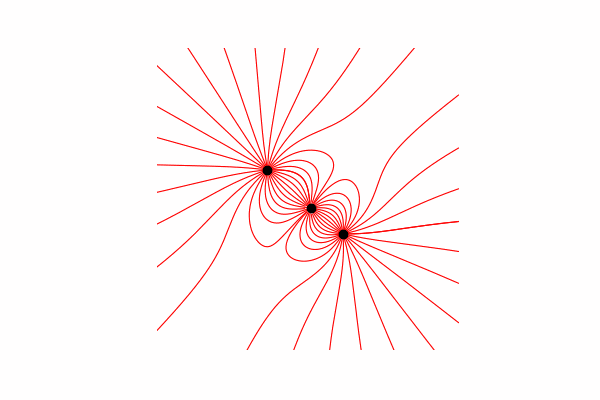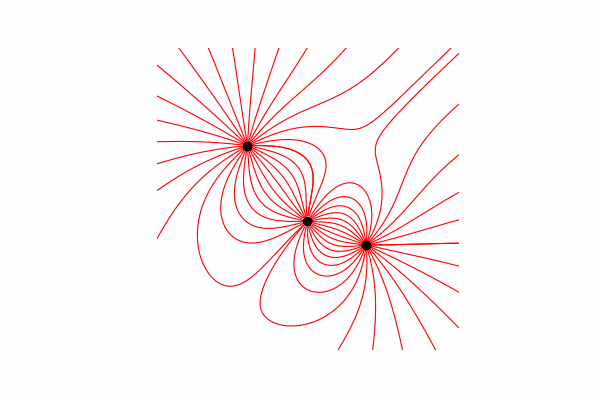

Der gesamte Code ist in Google Colab zu finden .

Theorie

Erstens brauchen wir ein kleines theoretisches Minimum zu diesem Thema. Beginnen wir damit, zu verstehen, was Spannungslinien sind und wie man sie zählt. Tatsächlich sind diese Linien die Verschmelzung vieler Spannungsvektoren, die wie folgt berechnet werden können: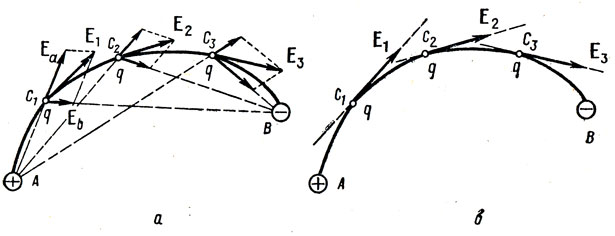

E = \frac{k * | q |}{r^{2}}

$E=\frac{k*|q|}{r^2}$ .

Bild

E Berechnungsmethode

Ich habe den Spannungsvektor durch die Ähnlichkeit von Dreiecken berechnet und dabei Projektionen auf die x- und y-Achse dx bzw. dy erhalten.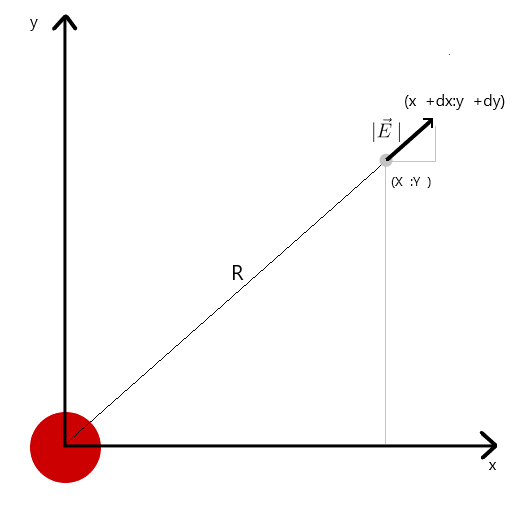

Aus der Ähnlichkeit folgt, dass der Radius des Vektors von der Ladung zum Punkt im Raum r und die Länge des Intensitätsvektors E gleich dem Verhältnis der Projektionen dieser Vektoren (x1 bzw. dx) sind.

\frac{R}{E} = \frac{x}{d x} = \frac{y}{d y}

$\frac{R}{E}=\frac{x}{dx}=\frac{y}{dy}$ . Formel des resultierenden Vektors

\vec{E} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{E}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{E}}_{i} |}{R_{i}} \end{matrix})

$\vec{E}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{E}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{E}_i|}{R_i} \end{array}\right) \qquad$
Mit diesem Wissen erhalten wir das erste Ergebnis.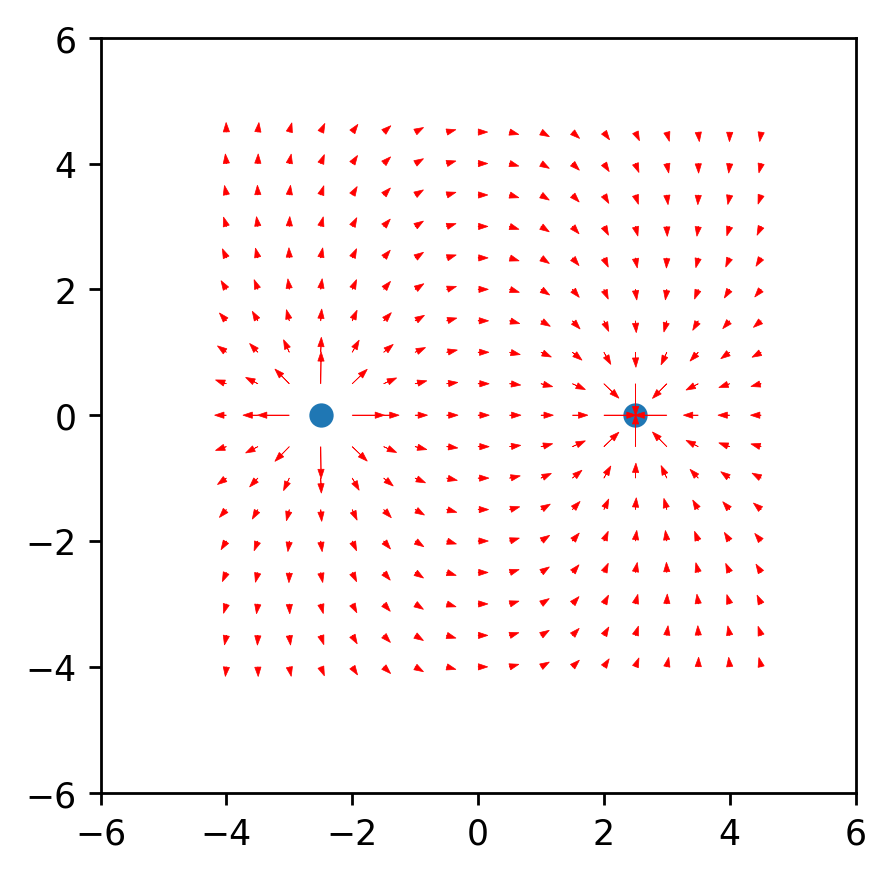

Projektionsberechnungsfunktion

def E(q_prop, xs, ys, nq): #q_prop=[[xq1, yq1, q1, mq1, vxq1, vyq1], [xq2, yq2, q2, mq2, vxq2, vyq2] ... ] 
    l=1
    k=9*10**9
    Ex=0
    Ey=0
    c=0
    for c in range(len(q_prop)):#                
        q=q_prop[c]
        r=((xs-q[0])**2+(ys-q[1])**2)**0.5
        dEv=(k*q[2])/r**2
        dEx=(xs-q[0])*(dEv/r)*l
        dEy=(ys-q[1])*(dEv/r)*l

        Ex+=dEx
        Ey+=dEy
    return Ex, Ey

Linienbauweise

Zuerst müssen Sie den Start- und Endpunkt festlegen, von dem aus die Linie und das Dokument ausgehen. Der Anfang sind Punkte auf einem Kreis mit einem Radius r um die Ladung, und die Endpunkte sind nicht mehr als r von den Ladungen entfernt.

Code für Startpunkte

theta = np.linspace(0, 2*np.pi, n)
mask=q_prop[ q_prop[:,2]>0 ]#    
for cq in range(len(mask)):
    qmask=mask[cq]
    xr = r_q*np.cos(theta)+qmask[0]# -    
    yr = r_q*np.sin(theta)+qmask[1]#

Es ist also erwähnenswert, dass die Leitungen nur aus positiven Ladungen gebaut werden.

Und schließlich der Bau von Linien. Dazu bauen wir die Linie des darin enthaltenen Spannungsvektors vom Startpunkt aus auf, aktualisieren den Startpunkt am Ende der konstruierten Linie und wiederholen, bis die oben genannten Endbedingungen erreicht sind.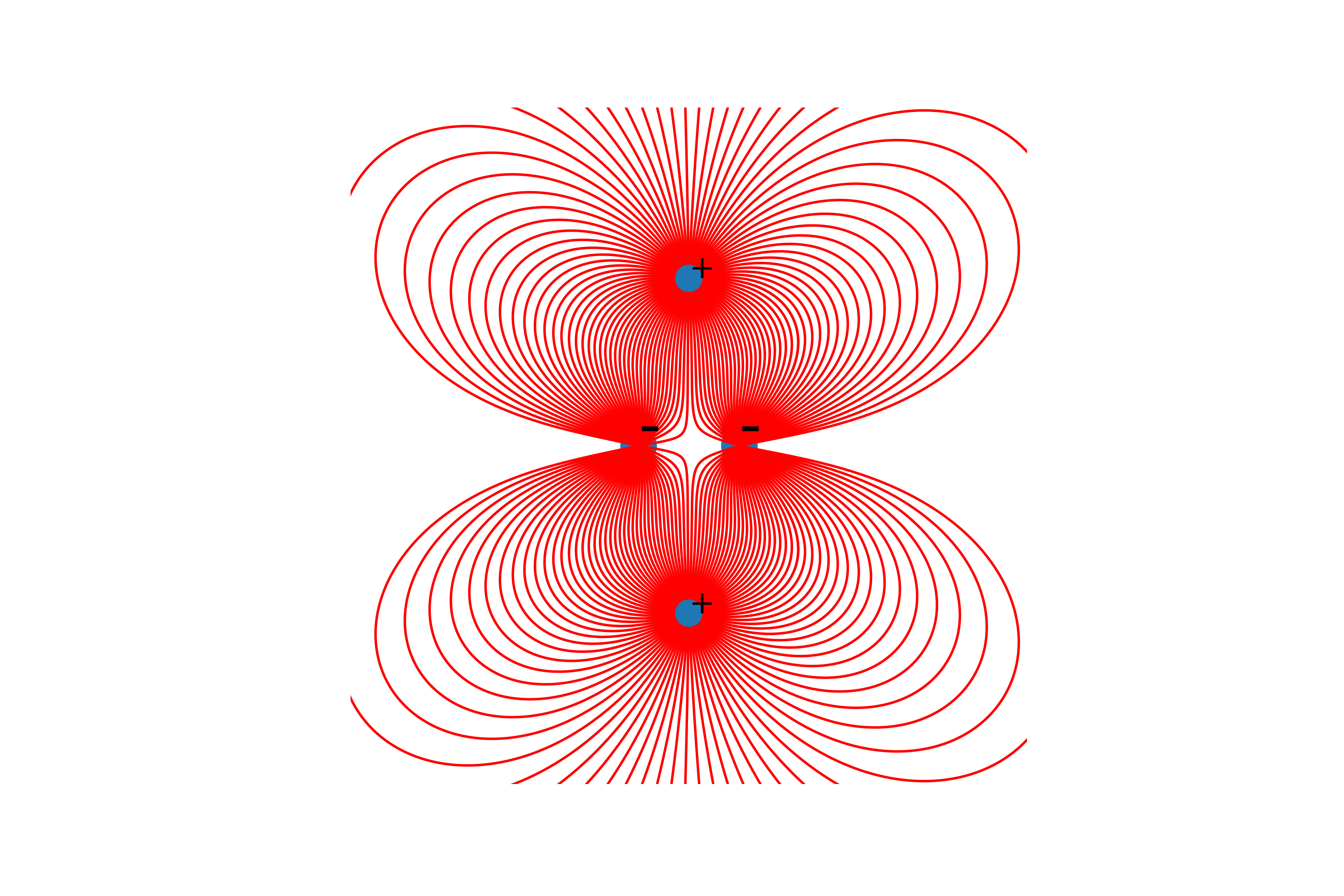

Linienkoordinatenberechnungsfunktion

def Draw(size, q_prop,r_q, n):
  
  linen=np.empty((np.count_nonzero(q_prop[:,2]>0),n, 2000000), dtype=np.float64)
  linen[:] = np.nan
  theta = np.linspace(0, 2*np.pi, n)
  mask=q_prop[ q_prop[:,2]>0 ][ q_prop[q_prop[:,2]>0][:,3]==1 ]
  for cq in range(len(mask)):
    qmask=mask[cq]
    x11 = r_q*np.cos(theta)+qmask[0]
    x22 = r_q*np.sin(theta)+qmask[1]
    for c in range(len(x11)):

      xs=x11[c]
      ys=x22[c]

      lines=np.empty((2,1000000), dtype=np.float64)
      lines[:]=np.nan
      stop=0
      nnn=0
      
      lines[0][nnn]=xs
      lines[1][nnn]=ys
      while  abs(xs)<size+2 and abs(ys)<size+2: 
        nnn+=1

        for cq1 in range(len(q_prop)):
          q=q_prop[cq1]
          if ((ys-q[1])**2+(xs-q[0])**2)**0.5<r_q/2 :
            stop=1
            break
        if stop==1:
          break
        dx, dy = E1(q_prop,xs,ys)

        xs+=dx
        ys+=dy
        lines[0][nnn]=xs
        lines[1][nnn]=ys
       
      linen[cq,c,:]=lines.reshape(-1)

  return linen

Interaktion zwischen Gebühren

Um ihre Interaktion widerzuspiegeln, ist es notwendig, ihre Koordinaten und Geschwindigkeit nach jeder kleinen Zeit dt zu ändern.

x + = \frac{E_{x} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{x} \cdot d t

$x+=\frac{E_x \cdot q \cdot dt^2}{2\cdot m} + v_x\cdot dt$

y + = \frac{E_{y} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{y} \cdot d t

$y+=\frac{E_y \cdot q \cdot dt^2}{2\cdot m} + v_y \cdot dt$

v_{x} + = \frac{E_{x} \cdot q \cdot d t}{m}

$v_x+= \frac{E_x \cdot q \cdot dt}{ m}$

v_{y} + = \frac{E_{y} \cdot q \cdot d t}{m}

$v_y+= \frac{E_y \cdot q \cdot dt}{ m}$

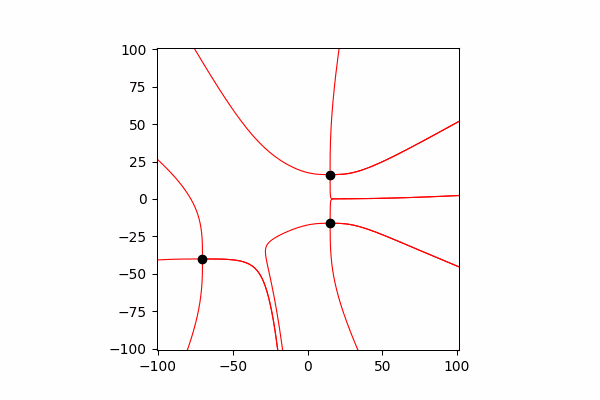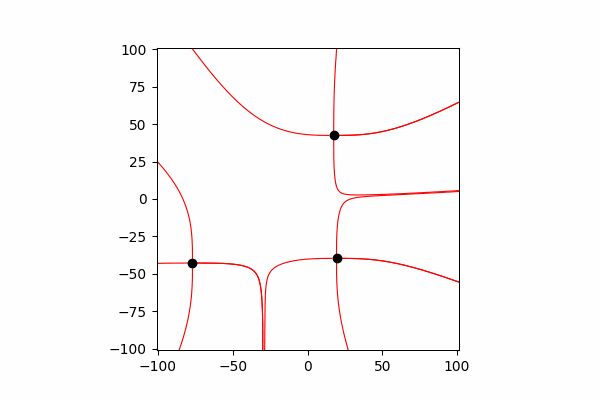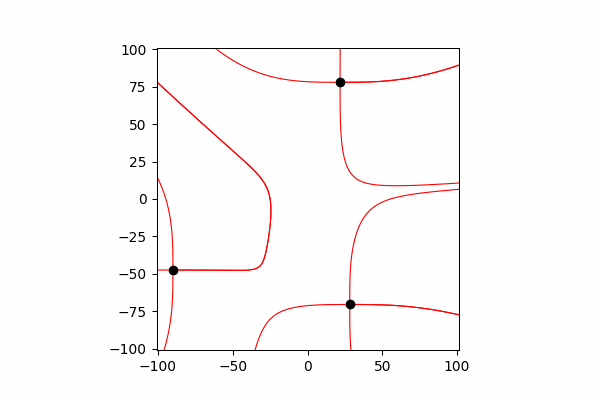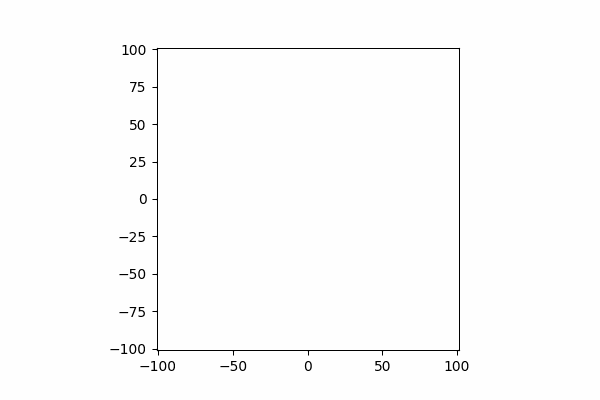
Funktion zum Aktualisieren von Koordinaten und Projektionen von Ladegeschwindigkeiten

def Update_all(q_prop):
  vx=0
  vy=0
  x=0
  y=0
  q_prop_1=np.copy(q_prop)
  for c in range(len(q_prop)):#         
    xs=q_prop[c][0]
    ys=q_prop[c][1]
    q =q_prop[c][2]
    m =q_prop[c][3]
    vx=q_prop[c][4]
    vy=q_prop[c][5]
    Ex, Ey= E(q_prop, xs, ys, c)

    x=(((Ex*q)/m)*dt**2)/2+vx*dt+xs
    y=(((Ey*q)/m)*dt**2)/2+vy*dt+ys
    vx+=((Ex*q)/m)*dt
    vy+=((Ey*q)/m)*dt
    #print(q_prop[c]-[x,y,q,m,vx,vy])
    q_prop_1[c]=[x,y,q,m,vx,vy]
  
  return q_prop_1#

Schwere

Basierend auf dem vorhandenen Code habe ich einen Simulator geschrieben, der die Bewegungen von Körpern unter dem Einfluss der Schwerkraft widerspiegelt. Änderungen im Code betreffen seitdem hauptsächlich die Spannungsfunktion Die Beschleunigung wird nun unter Verwendung einer ähnlichen Formel betrachtet.

g = \frac{G * m}{r^{2}}

$g=\frac{G*m}{r^2}$

\vec{g} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{g}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{g}}_{i} |}{R_{i}} \end{matrix})

$\vec{g}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{g}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{g}_i|}{R_i} \end{array}\right) \qquad$

Planeten starten von der x-Achse in Perihelentfernung und mit Perihelgeschwindigkeit. Alle Werte der Planeten und der Sonne (Masse, Entfernung, Extremitäten) aus dem Verzeichnis.

Animation für die ersten 4 Planeten + Sonne.

Warten auf Kritik und Vorschläge. Auf Wiedersehen.

Visualisierung von Spannungslinien und Bewegungen elektrostatischer Ladungen, Simulation der Planetenbewegung des Sonnensystems

Theorie

E Berechnungsmethode

Linienbauweise

Interaktion zwischen Gebühren

Schwere

More articles: