🤩 🏔️ ⚓️ Menschen treffen auf Empfehlungssysteme. Faktorisierung ⌛️ 🏤 👶🏿

Maschinelles Lernen hat unseren Alltag ziemlich durchdrungen. Einige sind nicht mehr überrascht, wenn sie über neuronale Netze in ihren Smartphones informiert werden. Einer der großen Bereiche dieser Wissenschaft sind Empfehlungssysteme. Sie sind überall: wenn Sie Musik hören, Bücher lesen, Fernsehsendungen oder Videos ansehen. Die Entwicklung dieser Wissenschaft findet in riesigen Unternehmen wie YouTube , Spotify und Netfilx statt . Natürlich werden alle wissenschaftlichen Errungenschaften in diesem Bereich sowohl auf den berühmten NeurIPS- oder ICML-Konferenzen als auch auf den etwas weniger bekannten RecSys veröffentlichtzu diesem Thema geschärft. Und in diesem Artikel werden wir darüber sprechen, wie sich diese Wissenschaft entwickelt hat, welche Methoden damals und heute in Empfehlungen verwendet werden und welche Mathematik dahinter steckt.

Ich wurde inspiriert, diesen Artikel zu schreiben, indem ich im StatML- Labor von Skoltech über Empfehlungssysteme arbeitete.

Warum und für wen dieser Artikel

Warum kann das für jeden von uns wichtig sein? Schauen Sie sich die folgende Liste an:

Videoempfehlungen : YouTube, Netlix, HBO, Amazon Prime, Disney +, Hulu, Okko
Audioempfehlungen : Spotify, Yandex.Music, Yandex.Radio, Apple Music
Produktempfehlungen: Amazon, Avito, Liter, MyBook
Suchempfehlungen: Google, Yandex, Bing, Yahoo, Mail
: Booking, Twitter, Instagram, ., , GitHub

, . , . , , YouTube.

( ), . , , . , ( ). -, . , -, , - . , . , , , , .

, , , , - . , (, , , ..). , .

, . : $U$ $I$ — . $r_{ui}$ $u$ $i$ . , , , , . :

D = {(u, i) | if \exists r_{u i}, u \in U, i \in I}

$\mathcal{D} = \{ (u, i) |\text{ if } \exists r_{ui}, u \in U, i \in I\}$

$f$ :

f (u, i) = {\hat{r}}_{u i} \approx r_{u i}

$f(u, i) = \hat{r}_{ui}\approx r_{ui}$

, $r_{ui}$ 1 5 ( ) : 1 -1 ( / )

3 :

Content-based (CB)
Collaborative filtering (CF)
Hybrid recommendations

. — , . : — , — , . . , : , ..

, . - , .

. , , , .

, , . . , , . .

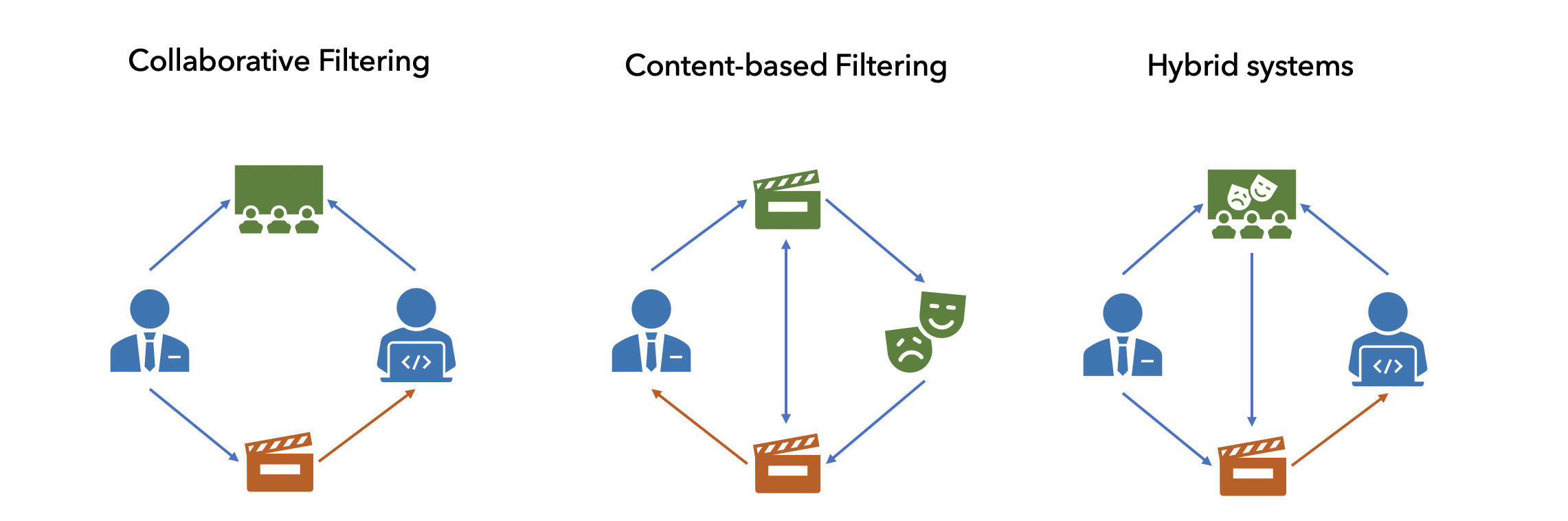
Matrix Factorization

, . : . .

:
- Singular Value Decomposition (SVD)
- Singular Value Decomposition with implicit feedback (SVD++)
- Collaborative Filtering with Temporal Dynamics (TimeSVD++)
- Weighted Matrix Factorization (WMF or ALS)
- Sparse Linear Methods (SLIM)
- Factorization Machines (FM)
:
- Probabilistic Matrix Factorization (PMF)
- Bayesian Probabilistic Matrix Factorization (BPMF)
- Bayesian Factorization Machines (BFM)
- Gaussian Process Factorization Machines (GPFM)

Singular Value Decomposition (SVD)

— SVD. $A$ $n \times m$ , $n = |U|$ , $m = |I|$ . $\mathcal{D}$ $A_{ui} = r_{ui}$ , . SVD , $A$ : $U,~\Sigma,~V$ . $k$ , $A$ .

A = U Σ V^{T}, A \approx \hat{A} = \hat{U} \hat{Σ} {\hat{V}}^{T} .

$A = U \Sigma V^T, \quad\quad\quad\quad A \approx \hat{A} = \hat{U} \hat{ \Sigma } \hat{V}^T .$

$Q$ $P$ . $A$ :

P = (\hat{U} \hat{Σ})^{T}, Q = {\hat{V}}^{T}, A \approx P^{T} \cdot Q .

$P = (\hat{U} \hat{ \Sigma })^T, \quad\quad Q = \hat{V}^T, \quad\quad\quad\quad A \approx P^T \cdot Q .$

r_{u i} \approx {\hat{r}}_{u i} = p_{u}^{T} q_{i} .

$r_{ui} \approx \hat{r}_{ui} = p^T_u q_i .$

, $p_u$ $q_i$ — $u$ $i$ - $k$ . . . :

Θ = {p_{u}, q_{i} | u \in U, i \in I} .

$\Theta = \{ p_u, q_i| u \in U, i \in I\} .$

c :

\sum_{(u, i) \in D} (r_{u i} - {\hat{r}}_{u i})^{2} + λ \sum_{θ \in Θ} ‖ θ ‖^{2} = \sum_{(u, i) \in D} (r_{u i} - p_{u}^{T} q_{i})^{2} + λ \sum_{u \in U} ‖ p_{u} ‖^{2} + λ \sum_{i \in I} ‖ q_{i} ‖^{2} .

$\sum_{(u, i) \in \mathcal{D}} (r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 = \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p^T_u q_i)^2 + \lambda\sum_{u \in U}\|p_u\|^2 + \lambda\sum_{i \in I}\|q_i\|^2 .$

, , , , . $\hat{r}_{ui}$ . (GD) (ALS). Habr- , . , , .

( SVD, SVD $_{bias}$ ). , , . . SVD . (bias):

{\hat{r}}_{u i} = μ + b_{u} + b_{i} + p_{u}^{T} q_{i},

$\hat{r}_{ui} =\mu + b_u + b_i + p^T_u q_i ,$

$b_u$ — , $b_i$ — , $\mu$ — . :

Θ = {μ, b_{u}, b_{i}, p_{u}, q_{i} | u \in U, i \in I} .

$\Theta = \{ \mu, b_u, b_i, p_u, q_i| u \in U, i \in I\} .$

SVD++

Factorization Meets the Neighborhood SVD . (explicit and implicit user feedback). $r_{ui}$ , . . : $R(u)$ — ( ) $N(u)$ — ( ).

SVD++ :

{\hat{r}}_{u i} = μ + b_{u} + b_{i} + q_{i}^{T} (p_{u} + | N (u) |^{- 1 / 2} \sum_{j \in N (u)} y_{j}) .

$\hat{r}_{ui} =\mu + b_u + b_i + q^T_i \left( p_u + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) .$

Θ = {μ, b_{u}, b_{i}, p_{u}, q_{i}, y_{i} | u \in U, i \in I} .

$\Theta = \{ \mu, b_u, b_i, p_u, q_i, y_i| u \in U, i \in I\} .$

, $N(u)$ $R(u)$ , .. $R(u) \subset N(u)$ . (item-item recommendation).

Asymmetric-SVD

SVD++ . . :

{\hat{r}}_{u i} = b_{u i} + q_{i}^{T} (| R (u) |^{- 1 / 2} \sum_{j \in R (u)} (r_{u j} - b_{u j}) x_{j} + | N (u) |^{- 1 / 2} \sum_{j \in N (u)} y_{j}),

$\hat{r}_{ui} = b_{ui} + q^T_i \left( |R(u)|^{-1/2} \sum_{j \in R(u)} (r_{uj} - b_{uj})x_j + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) ,$

$b_{ui} = \mu + b_u + b_i$

TimeSVD++

TimeSVD++. (MovieLens, Netflix) , . , . Collaborative Filtering with Temporal Dynamics SVD++ :

{\hat{r}}_{u i} (t) = μ + b_{u} (t) + b_{i} (t) + q_{i}^{T} (p_{u} (t) + | R (u) |^{- 1 / 2} \sum_{j \in R (u)} y_{j}) .

$\hat{r}_{ui}(t) =\mu + b_u(t) + b_i(t) + q^T_i \left( p_u(t) + |R(u)|^{-1/2} \sum_{j \in R(u)} y_j \right) .$

Lassen Sie uns genau herausfinden, wie sich die Zeit auf die einzelnen Begriffe auswirkt:
Item Bias: Wenn Sie das Zeitintervall, in dem Bewertungen vorgenommen wurden, in Segmente unterteilen (30 Teile werden in der Arbeit vorgeschlagen) und Ihre eigenen Parameter hinzufügen $b_{i,\text{Bin}(t)}$ für jedes Produkt, die abhängig vom Intervall ausgewählt werden, in dem die Variable $t$ ::

b_{i} (t) = b_{i} + b_{i, Bin (t)}

$b_i(t) = b_i + b_{i, \text{Bin}(t)}$

User Bias: Bei der Analyse der Daten von Neflix haben wir festgestellt, dass jeder Benutzer durchschnittlich nur 40 Tage Zeit hat, um die Bewertungen abzugeben. Deshalb werden wir wie bei Waren handeln und unsere eigenen Parameter hinzufügen

b_{u, t}

$b_{u, t}$ für jeden Benutzer. Wir fügen eine lineare Abhängigkeit von der Zeit hinzu - wir führen einen zusätzlichen Begriff ein

α_{u}

$\alpha_u$ mit Abschreibungsquote:

b_{i} (t) = b_{i} + α_{u} \cdot {dev}_{u} (t) + b_{u, t} {dev}_{u} (t) = sign (t - t_{u}) \cdot | t - t_{u} |^{β}

$b_i(t) = b_i + \alpha_u \cdot \text{dev}_u(t) + b_{u, t} \quad\quad\quad\quad \text{dev}_u(t) = \text{sign}(t - t_u) \cdot |t - t_u|^{\beta}$

.
Es gibt andere Möglichkeiten, wie Sie Benutzern eine Zeitabhängigkeit hinzufügen können: Dies wird im Artikel
Benutzereinbettungen ausführlicher beschrieben : Wir werden für jede Komponente unserer latenten Darstellung einen ähnlichen Trick hinzufügen

p_{u} (t) = (p_{u 1} (t), \dots, p_{u f} (t))^{T}

$p_u(t) = (p_{u1}(t), \dots, p_{uf}(t))^T$ ::

p_{u k} (t) = p_{u k} + α_{u k} \cdot {dev}_{u} (t) + p_{u k, t} .

$p_{uk}(t) = p_{uk} + \alpha_{uk} \cdot \text{dev}_u(t) + p_{uk, t}.$

Gewichtete Matrixfaktorisierung (WMF) und alternierende kleinste Quadrate (ALS)

Eines der Hauptprobleme von SVD ist die Verwendung nur einer expliziten Antwort des Benutzers. Dieses Problem wurde teilweise in SVD ++ gelöst . Es gibt aber noch einen anderen Weg - die Weighted Matrix Factorization ( WMF ). In diesem Artikel wurde vorgeschlagen, das Modell fast nicht zu ändern ( $\hat{r}_{ui} = p^T_u q_i$ ) und ändern Sie den Lernprozess. Für Bewertungen zuweisen $r_{ui}$ das wissen wir nicht (d. h. für Paare $(u, i) \notin \mathcal{D}$ ) der Wert ist 0. Und dann für jedes Paar $(u, i)$ Geben Sie den Parameter ein $c_{ui}$ , $r_{ui}$ . , . - . YouTube , . , , , . , , , :

\sum_{(u, i)} c_{u i} (r_{u i} - {\hat{r}}_{u i})^{2} + λ \sum_{θ \in Θ} ‖ θ ‖^{2} .

$\sum_{(u, i)} c_{ui}(r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 .$

: $c_{ui} = 1 + \alpha r_{ui}$ . : $r_{ui}>0$ $r_{ui} = 0$ . $\alpha$ $\alpha = 40$ .

, (ALS) . WMF, ALS, .

Fast Alternating Least Squares

ALS , eALS . , . , . .

, $c_{ui}$ ALS :

c_{u i} = c_{i} + α r_{u i}, c_{i} = c_{0} \frac{f_{i}^{β}}{\sum_{j \in I} f_{j}^{β}},

$c_{ui} = c_i + \alpha r_{ui}, \quad\quad\quad\quad c_i = c_0 \frac{f_i^{\beta}}{\sum_{j \in I} f_j^{\beta}} ,$

$c_0$ $\beta$ , .

Sparse Linear Methods (SLIM)

Sparse Linear Methods (SLIM) . , SVD . . SLIM :

{\hat{a}}_{u i} = a_{u}^{T} w_{i} \hat{A} = A W

$\hat{a}_{ui} = a^T_u w_i \quad\quad\quad\quad \hat{A} = AW$

$W \in \mathbb{R}^{m \times m}$ . : $W \geq 0$ $\text{diag}(W) = 0$ . :

\frac{1}{2} ‖ A - A W ‖_{F}^{2} + \frac{β}{2} ‖ W ‖_{F}^{2} + λ ‖ W ‖_{1}

$\frac{1}{2}\|A - AW\|^2_F + \frac{\beta}{2}\|W\|^2_F + \lambda\|W\|_1$

$W$ .

Factorization Machines (FM)

, Factorization Machines (FM). , ( 2- ). :

\hat{r} (x) = w_{0} + \sum_{i = 1}^{n} w_{i} x_{i} + \sum_{i = 1}^{n} \sum_{i = j + 1}^{n} v_{i}^{T} v_{j} x_{i} x_{j}, w_{0} \in R w \in R^{n} V \in R^{n \times k} .

$\hat{r}(x) = w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{i=j+1}^{n} v^T_i v_j ~ x_i x_j, \quad\quad\quad\quad w_0 \in \mathbb{R} ~~~ w \in \mathbb{R}^n ~~~ V \in \mathbb{R}^{n \times k} .$

(SGD) ( ). , $x$ $(u, i)$ . . , — . — ( ). ( ).

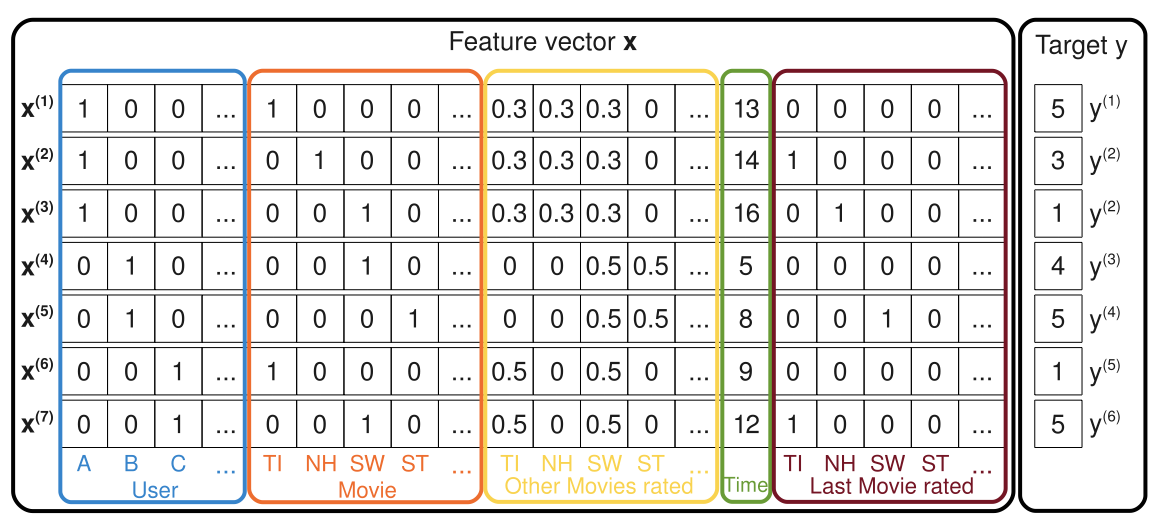
, SVD, SVD++ — FM. SVD , :

n = | U \cup I |, x_{j} = δ (j = u \lor j = i) .

$n = | U \cup I |, \quad\quad\quad x_j = \delta (j = u ~\lor~ j = i) .$

$\delta$ — . .. $x$ $u$ $i$ . FM :

\hat{r} (x) = w_{0} + w_{u} + w_{i} + v_{u}^{T} v_{i} .

$\hat{r}(x) = w_0 + w_u + w_i + v^T_u v_i .$

, $x$ : , . , , , , , , . .

Probabilistic Matrix Factorization (PMF)

, , , .

(PMF), . , SVD: $p_u$ $q_i$ — . , :

p (r | P, Q, σ) = \prod_{(u, i) \in D} N (r_{u i} | g (p_{u}^{T} q_{i}), σ^{2}),

$p(r | P, Q, \sigma) = \prod_{(u, i) \in \mathcal{D}}\mathcal{N}(r_{ui}| g(p_u^Tq_i), \sigma^2) ,$

$\mathcal{N}$ — , a $g(x) = \frac{1}{1 + e^{-x}}$ — (). , , :

p (P | σ_{p}) = \prod_{u \in U} p (p_{u} | 0, σ_{p}^{2} I), p (Q | σ_{q}^{2}) = \prod_{i \in I} p (q_{i} | 0, σ_{q}^{2} I) .

$p(P| \sigma_p) = \prod_{u \in U} p(p_u| 0, \sigma^2_p \mathbf{I}), \quad\quad\quad\quad p(Q| \sigma^2_q) = \prod_{i \in I} p(q_i| 0, \sigma_q^2 \mathbf{I}) .$

( ) , :

\frac{1}{2} \sum_{(u, i) \in D} (r_{u i} - p_{u}^{T} q_{i})^{2} + \frac{λ_{p}}{2} \sum_{u \in U} ‖ p_{u} ‖^{2} + \frac{λ_{q}}{2} \sum_{i \in I} ‖ q_{i} ‖^{2},

$\frac{1}{2} \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p_u^T q_i)^2 + \frac{\lambda_p}{2} \sum_{u \in U} \|p_u\|^2 + \frac{\lambda_q}{2} \sum_{i \in I} \|q_i\|^2 ,$

$\lambda_p = \frac{\sigma_p}{\sigma}$ $\lambda_q = \frac{\sigma_q}{\sigma}$ — . , SVD , .

Constrained PMF

PMF Constrained PMF. , SVD SVD++. , , $p_u$ :

p_{u} + \frac{\sum_{i \in R (u)} y_{i}}{| R (u) |},

$p_u + \frac{\sum_{i \in R(u)} y_i}{|R(u)|} ,$

$R(u)$ — , $u$ .

Bayesian Probabilistic Matrix Factorization (BPMF)

PMF BPMF. PMF , , . :

p (P | μ_{p}, Λ_{p}) = \prod_{u \in U} p (p_{u} | μ_{p}, Λ_{p}), p (Q | μ_{q}, Λ_{q}) = \prod_{i \in I} p (q_{i} | μ_{q}, Λ_{q}) .

$p(P| \mu_p, \Lambda_p) = \prod_{u \in U} p(p_u| \mu_p, \Lambda_p) ,\quad\quad\quad\quad p(Q| \mu_q, \Lambda_q) = \prod_{i \in I} p(q_i| \mu_q, \Lambda_q) .$

$\Theta_p = \{ \mu_p, \Lambda_p \}$ $\Theta_q = \{ \mu_q, \Lambda_q \}$ - $\Theta_0 = \{ \mu_0, \nu_0, W_0 \}$ . , .

Bayesian Factorization Machines (BFM)

, Bayesian, . , $\Theta = \{ w_0, w_i, v_i\} .$ , - . : $\Theta_H = \{ \lambda_{\theta}, \mu_{\theta} | \theta \in \Theta \}$ . .

Gaussian Process Factorization Machines (GPFM)

GPFM . $f$ $\theta$ . $\theta_u$ , , :

{\hat{r}}_{u i} = f (q_{i}, θ_{u})

$\hat{r}_{ui} = f(q_i, \theta_u)$

, . , $f$ , . , , , .

: Bayesian Personalized Ranking (BPR)

BPR , "". , BPR — , , Bayesian Personalized Ranking. . , , $i$ $j$ $u$ . $(u, i)$ $r_{ui}$ $(u, i, j)$ $i$ $j$ ((+) $i$ , $j$ (-) ). $\mathcal{D}_S$ . . ( personalized ):

p (i <_{u} j | Θ) = σ ({\hat{r}}_{u i j} (Θ)),

$p(i <_u j | \Theta) = \sigma(\hat{r}_{uij}(\Theta)) ,$

$\sigma$ — , a $\hat{r}_{uij}$ — . (MLE), , :

min_{Θ} \sum_{(u, i, j) \in D_{S}} \ln σ ({\hat{r}}_{u i j}) - λ ‖ Θ ‖^{2}

$\min_{\Theta} \sum_{(u, i, j) \in \mathcal{D}_S}\ln{\sigma(\hat{r}_{uij})} - \lambda \|\Theta\|^2$

(SGD):

Θ \leftarrow Θ + α (\frac{e^{- {\hat{r}}_{u i j}}}{1 + e^{- {\hat{r}}_{u i j}}} \cdot \frac{\partial}{\partial Θ} {\hat{r}}_{u i j} + λ Θ)

$\Theta \leftarrow \Theta + \alpha\left(\frac{e^{-\hat{r}_{uij}}}{1 + e^{-\hat{r}_{uij}}} \cdot \frac{\partial}{\partial \Theta}\hat{r}_{uij} + \lambda \Theta \right)$

, . , , . SVD:

{\hat{r}}_{u i j} = {\hat{r}}_{u i} - {\hat{r}}_{u j} {\hat{r}}_{u i} = p_{u}^{T} q_{i}

$\hat{r}_{uij} = \hat{r}_{ui} - \hat{r}_{uj} \quad\quad\quad\quad \hat{r}_{ui} = p_u^T q_i$

\frac{\partial}{\partial Θ} {\hat{r}}_{u i j} = {\begin{cases} (q_{i k} - q_{j k}) if θ = p_{u k} \\ p_{u k} if θ = q_{i k} \\ - p_{u k} if θ = q_{j k} \end{cases}

$\frac{\partial}{\partial \Theta}\hat{r}_{uij} =\begin{cases} (q_{ik} - q_{jk})~~~\text{if } \theta = p_{uk}\\ p_{uk}~~~~~~~~~~~~~~~\text{if } \theta = q_{ik}\\ -p_{uk}~~~~~~~~~~~~\text{if } \theta = q_{jk} \end{cases}$

BPR ( ) , . , . . , (pairwise approach) (pointwise approach). . , 5 , . , , . — BPR - , . , .

Show must go on

Dieses Mal haben wir viele Faktorisierungsmethoden in Empfehlungssystemen diskutiert , aber die Graphen- und Neuronalen Netze , die auch viele interessante Dinge enthalten , blieben unberührt .

Menschen treffen auf Empfehlungssysteme. Faktorisierung