تخيل الموقف - أنت تشتري سيارة ، ويتوفر لك خياران: الدفع على أقساط لعدة أشهر أو سداد المبلغ بالكامل على الفور وبخصم صغير. أيهما أكثر ربحية؟أو ، على سبيل المثال ، تريد تقديم مساهمة لمدة عام. يمكنك تحديد المدة بأكملها بنسبة عالية أو لفترات قصيرة فردية بسعر أقل. أيهما أفضل وكم؟جميع الإجابات تحت القط. ومرحبا بكم في عالم حيث الوقت هو المال دائما. كنت تعرف ذلك من قبل ، ولكن الآن - بالتفصيل والأمثلة.اسمي ماريا أبراشكينا ، أنا عالم رياضيات ومالك منتج في فريق حساب مخاطر المحفظة. وكذلك أحد مؤلفي دورة الفيديو عن الرياضيات المالية (الجزء الأول - أنواع حساب الفائدة ، الجزء الثاني - الخصم ، الجزء الثالث - أسعار الفائدة الآجلة ). في هذا المنشور سأتحدث عن قيمة المال وأسعار الفائدة والسندات . ستساعدك هذه المعرفة في المستقبل على اتخاذ قرارات مالية بناءً على حساب دقيق ، باستخدام رياضيات بسيطة.رقم 1. القيمة الزمنية للنقود. أنواع الفائدة المستحقة
أولاً ، لنتحدث عن القيمة الزمنية للنقود ، أو القيمة الزمنية للنقود (TVM) ، ولماذا يكون للنقود قيمة وأنواع الفائدة الموجودة.تُظهر الصورة أدناه قائمة بالأفلام ذات الحد الأقصى لشباك التذاكر.هل يمكننا مقارنتها بهذه الأرقام؟ بالنظر إلى أن الأفلام تم إصدارها في سنوات مختلفة ، فمن غير المرجح أن تكون هذه المقارنة صحيحة. كيف تكوندعونا نلقي نظرة على مثال أبسط. افترض أن لديك ألف روبل ، وأطلب منك هذا المبلغ بالدين. كم تريد مني أن أعطيك في السنة؟ ربما ستعتقد أنه بالنسبة لهذا الألف روبل ، يمكنك الآن شراء زجاجة من النبيذ اللذيذ أو أي شيء آخر. يمكنك أيضًا أن تفترض أنه بعد مرور عام على نفس الألف روبل ، من غير المحتمل أن تتمكن من شراء هذا المنتج بسبب التضخم. بالإضافة إلى ذلك ، هناك خطر من أنني لن أعيد المال. لذلك ، على الأرجح ، ستحتاج إلى تعويض عن حقيقة أنك لن تشتري زجاجة من النبيذ أو أي شيء آخر. تحتاج أيضًا إلى حافز لتبرير خطر عدم إعادة الأموال إليك. ربما ستطلب مني إعادة المال مع نوع من البدل ، أي بنسبة مئوية.لذا ، فإن المال له قيمة لأن مالكه يريد تعويضًا عن حقيقة أنه لا يستطيع شراء أي منتج أو خدمة ، وخطر تحمله ، وإعطاء المال في الدين.
في لغة الرياضيات ، سيبدو الأمر كما يلي:PV = 1000الآن تعطيني ألف روبل. تشير إلى أنه PV (Present Value). لنفترض أن المعدل (r)هو 5٪ ، وتعطيني المال لمدة عام واحد. ثم إعادة المال FV (Future Value)، يجب أن أضيف 50 روبل إلى المبلغ الأصلي.إذا قمت بكتابة هذه الصيغة بشكل عام ، فإن القيمة المستقبلية تساوي مبلغ الدين مضروبًا في واحد بالإضافة إلى سعر الفائدة.ولكن ماذا لو تم احتساب الفائدة أكثر من مرة في السنة ، ولكن في كثير من الأحيان؟ أو ماذا لو تراكمت الفائدة لمدة سنتين أو ثلاث أو عشر سنوات؟ في هذه الحالة ، نحتاج دائمًا إلى توضيح كيفية تراكم الفائدة ، في نهاية المدة أو مع بعض التكرار وعدد السنوات.فائدة بسيطة
ضع في اعتبارك المثال حيث يتم استحقاق الفائدة في نهاية مدة الإيداع. ستكون القيمة المستقبلية مساوية للقيمة الحالية بالإضافة إلى القيمة الحالية مضروبة في معدل الفائدة السنوي. سيتم إضافة سعر الفائدة السنوي إلى مبلغ الوديعة لدينا عدة مرات لعدد السنوات التي قدمنا فيها مساهمة.النتيجة - القيمة الحالية مضروبة في مجموع واحد مضافًا إليه سعر الفائدة (r)مضروبًا في عدد سنوات المساهمة (T). تسمى طريقة حساب الفائدة هذه بفائدة بسيطة .إذا تم احتساب سعر الفائدة كل عام ، فستبدو الصيغة مختلفة.
النظر في الوضع مع الاستحقاق على مدى عدة سنوات. نعتقد أن سعر الفائدة الحالي طوال الفترة سيكون هو نفسه. ثم تأخذ الصيغة الشكل التالي: القيمة الحالية مضروبة في مجموع الوحدة بالإضافة إلى سعر الفائدة ، ثم مرة أخرى في مجموع الوحدة وسعر الفائدة ، إلخ. اضرب عدة مرات في عدد سنوات المساهمة. بشكل عام ، ستبدو الصيغة كما يلي:يرجى ملاحظة أنه في الحالة الأولى ، يتم إضافة مبلغ الفائدة إلى وديعتنا كل عام (كما في المثال الأول ، حيث تمت إضافة 50 روبل إلى مبلغ الإيداع) ، ففي حالة فرض رسوم سنوية بقيمة 50 روبل تمت إضافتها في الفترة الأولى ، فإننا نفرض رسومًا في كل مرة نسبه مئويه.من المهم دائمًا الانتباه إلى كيفية حساب الفائدة. يمكن أن تتراكم الفائدة ليس مرة واحدة فقط في السنة ، ولكن أيضًا مرة واحدة كل ستة أشهر ، كل يوم. ومن حيث المبدأ ، لا شيء يمنعنا من تحصيل هذه النسب بشكل مستمر.استحقاق الفائدة المستمرة
دعونا نلقي نظرة على كيف ستبدو صيغة حساب الفائدة أكثر من مرة في السنة. في هذه الحالة ، ستكون القيمة المستقبلية مساوية للقيمة الحالية مضروبة في مبلغ واحد بالإضافة إلى معدل الفائدة السنوي مقسومًا على عدد فترات الاستحقاق في السنة (n)في الدرجة nT. إذا تم عمل الاستحقاقات كل ستة أشهر ، ثم n=2إذا كان كل يوم ، ثم n=365.كيف ستبدو الصيغة إذا أردنا تحقيق الفائدة بشكل مستمر؟ هنا عليك أن تتذكر الرياضيات المدرسية. ستكون الصيغة كما يلي:من أجل جعل حدودنا على شكل مناسب ، نحتاج إلى إجراء استبدال. ونتيجة لذلك نحصل على ما يلي:بالنظر إلى أن حدنا يساوي رقم أويلر (e = 2.71) ، يتم تحويل صيغتنا إلى تعبير بسيط للغاية. يتم ضرب القيمة الحالية لمساهمتنا في الأس ، والتي يتم رفعها إلى الحد الذي يمثله منتج سعر الفائدة وعدد السنوات التي تراكمت فيها حصتنا.دعنا نقارن كيف تبدو المدفوعات حسب تواتر المستحقات. يوضح الجدول القيمة المستقبلية لمساهمة مائة ألف روبل ، والتي يتم طرحها لمدة عشر سنوات بمعدل عشرين بالمائة.كما ترى ، سيتلقى المودع 300 ألف روبل في حالة إجراء الاستحقاقات في نهاية مدة الإيداع.وبالتالي ، فإن مبلغ الوديعة عند حساب الفائدة سنويًا يضاعف مبلغ الوديعة عند دفع الفائدة مرة واحدة في نهاية المدة.
إذا تم عمل المستحقات بشكل مستمر ، فإن مبلغ الإيداع هو أكثر من 700 ألف روبل مقابل 300 ألف روبل مع حساب فائدة بسيط.يوضح الرسم البياني أدناه بوضوح كيف ينمو المبلغ الإجمالي للودائع بطرق مختلفة لحساب الفائدة.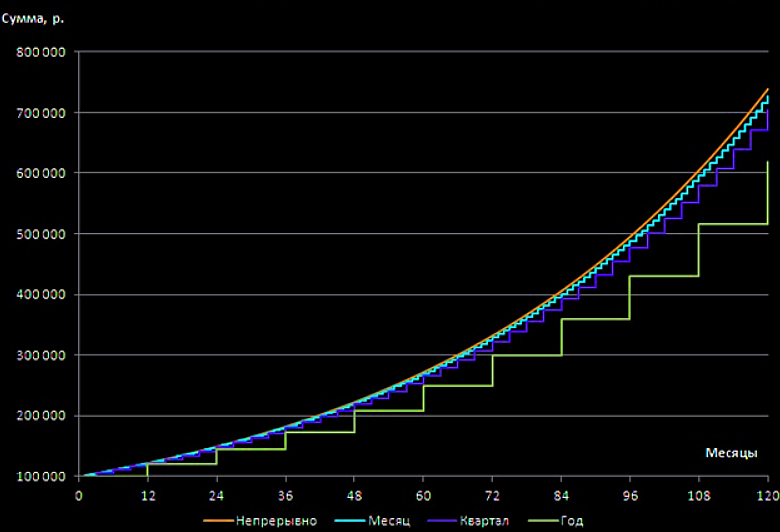
من هذا من الضروري الاستنتاج:عند اختيار مساهمة ، من المهم أن ننظر ليس فقط في حجم سعر الفائدة ، ولكن أيضًا في وتيرة استحقاق الفائدة. سعر الفائدة المرتفع ليس دائمًا مفيدًا حقًا.
لذلك ، قبل القيام باختيارك ، من المنطقي إجراء حسابات صغيرة لمعرفة المبلغ الإجمالي للمساهمة في ظل ظروف معينة.# 2 الخصم (يساعد على فهم أيهما أفضل: خذ خطة تقسيط أو ادفع الآن بخصم)
درسنا ما هي المعدلات وما هي طرق حساب الفائدة. إذا تم دفع الفائدة في نهاية مدة الإيداع ، فإن الفائدة تسمى بسيطة ، إذا تم دفع الفائدة في بعض الفترات ، فإن هذه الفائدة تسمى معقدة .دعونا حل المشكلة العكسية. لنفترض أننا نعرف المبلغ الذي سيتم دفعه لنا في المستقبل (على سبيل المثال ، وعدنا أحد الأشخاص بدفع ثمن منتج ما). نحن نعلم أيضًا ما هو سعر الفائدة الآن. كيف نحسب السعر الحالي لهذا المنتج؟كما ذكرنا سابقًا ، فإن القيمة المستقبلية لمبلغ الدفع ستكون مساوية للقيمة الحالية مضروبة في قيمة واحدة بالإضافة إلى سعر الفائدة. إذا عبرنا عن القيمة الحالية من هذه الصيغة ، فسوف تساوي القيمة المستقبلية مقسومة على واحد بالإضافة إلى سعر الفائدة.إذا تراكمت الفائدة مع بعض الفترات الدورية ، فستبدو الصيغة بشكل عام كما يلي:T- هذا هو عدد فترات دفع رسوم الفائدة. عملية قسمة القيمة المستقبلية على قيمة واحدة ، بالإضافة إلى سعر الفائدة ، إلى درجة Tتسمى الخصم . والعامل ، الوحدة مقسومة على مجموع الوحدة بالإضافة rإلى الطاقة T، يسمى معامل الخصم .دعنا نعود إلى المهمة التي من الأفضل أن تختار قسطها. اعتمادًا على طريقة المكافأة ، قد يختلف مبلغ المدفوعات. ومع ذلك ، ليس من الواضح دائمًا الطريقة الأفضل. لإعطاء الإجابة الصحيحة ، من الضروري حل مشكلة رياضية. لنفترض أن لدينا الفرصة لأخذ 105 ألف روبل في نهاية العام بسعر فائدة 5 في المائة. أو يمكننا اختيار طريقة أخرى للمكافأة عندما نتلقى 50 ألف روبل كل ستة أشهر بنفس سعر الفائدة.قارن بين هاتين الدفعتين. للقيام بذلك ، نحسب القيمة الحالية لكل من هذه المدفوعات. باستخدام الصيغة لإيجاد القيمة الحالية ، نحتاج إلى خصم 105 ألف بمعدل خمسة بالمائة (في هذه الحالة ، T = 1). نحصل على 100 ألف.للعثور على القيمة الحالية للمدفوعات كل ستة أشهر ، نحتاج إلى خصم 50000 روبل (التي سنحصل عليها في غضون ستة أشهر) بمعدل شهرين ونصف في المئة (لأن الاستحقاق يحدث فقط في الأشهر الستة الأولى. بالمعنى الدقيق للكلمة ، فإن معدل 6 أشهر لا يساوي نصف المعدل السنوي. N (1 + x) (1 + x) = N (1 + 0.05) => x = 2.4695٪ نستثمر لمدة 6 أشهر ، ثم مرة أخرى لـ 6 وهذا مطابق للاستثمار لمدة عام) ، خمسة بالمائة سنويًا ، مقسومًا على اثنين زائدا 50 الف مستلمة في نهاية العام ونقوم بخصمها بمعدل 5 بالمئة. نتيجة للحسابات ، نحصل على سعر الدفعة الأولى لمدة ستة أشهر بمبلغ 48،780 روبل 49 كوبيل والدفعة الثانية - 47،619 روبل 5 كوبيل. كمية الأشياء الثمينة هي 96،399 روبل 54 كوبيل.من الواضح أن اقتراح تلقي 105 ألف روبل في السنة أكثر ربحية من الحصول على 50 ألف روبل كل ستة أشهر. على الرغم من الحدس ، قد يبدو لك أن الاختلاف غير ذي أهمية ، على الرغم من حقيقة أنك ستتلقى الأموال بشكل أسرع. تقول لنا الرياضيات إن الأمر ليس كذلك.إنه أكثر ربحية الحصول على 105 ألف روبل من خلال الانتظار لفترة أطول.
يعمل هذا المبدأ عند تقييم مواقف الحياة المختلفة.على سبيل المثال ، عندما يُعرض عليك شراء سيارة بالتقسيط أو دفع المبلغ بالكامل الآن مع نوع من الخصم. تحتاج إلى أخذ المبلغ المستقبلي الذي تدفعه ، وإحضاره إلى القيمة الحالية ، ثم مقارنة المدفوعات التي تحدث في نفس الوقت.
في هذه الحالة ، ستكون المقارنة صحيحة.# 3 أسعار الفائدة الآجلة
لنفترض أننا نتفق على سعر الفائدة. عند سعر الفائدة هذا ، في السنة سأقترض المال منك ، والذي سأقوم بسداده خلال عامين ، بالإضافة إلى الفائدة. ما يجب أن يكون سعر الفائدة لكي تكون عادلة؟ سنصف هذا المثال بمزيد من التفصيل.نحن الآن في الوقت صفر. في غضون عام ، xسآخذ المال منك بمعدل وأعيده إليك في غضون عامين. كيف تحسب العطاء x؟ لدينا عدة خيارات. يمكنك الآن وضع الأموال بمعدل r1 في السنة ، ثم إعادة استثمارها بمعدل x.أو ضع المال على الفور بمعدل r2 لمدة عامين.هناك شرط عدم المراجحة في السوق المالية . تقول أنه إذا تلقينا في نهاية المدة نفس المدفوعات ، فعندئذٍ بالنسبة للأدوات ذات المخاطر نفسها ، فيجب أن يكون المبلغ الأولي هو نفسه. لنوقع عليه أيضًا. ستكون القيمة المستقبلية لخيار الاستثمار الأول FV1 مساوية للقيمة الحالية مضروبة في مجموع واحد و rT1 (نفترض أن لدينا حساب فائدة بسيط).لحظة الوقت T1 تساوي سنة واحدة. بعد ذلك ، سنقوم بإعادة استثمار المبلغ ، وسنضع فترة من T2 - T1 ، مضروبة في سعر الفائدة لدينا x. T2 - هذه نقطة زمنية ، في حالتنا ، سنتان.أو القيمة مستقبل FV2 وتساوي القيمة الحالية PVمضروبة واحد زائد r2 مرات T2 . وفقًا لشرط عدم التحكيم ، يجب أن يساوي FV1 FV2 .من هذا نحصل على ما يلي:الصيغة معقدة للغاية. دعنا نحسب مثالًا باستخدام هذه الصيغة ، ثم نفكر فيما يمكننا القيام به لجعله يبدو أبسط.ليكن سعر الفائدة لدينا r1 = 4٪ ؛ r2 = 6٪. في هذه الحالة لدينا ما يلي:x=(1+0,06*2)/(1+0,04*1)-1 = 1,077-1 = 0,077 = 7,7%
قد يبدو غريباً أن المعدل لمدة عامين يساوي ستة بالمائة ، ولعام واحد يساوي أربعة بالمائة ، ومن سنة إلى سنتين نحصل على معدل أكثر من سبعة بالمائة. هذا يفسر كالتالي. نظرًا لأن لدينا في العام الأول معدلًا سنويًا أقل من عامين ، في السنة التالية يجب أن يكون أعلى من هذين المعدلين. هذا ضروري من أجل تعويض نقص الفائدة في السنة الأولى ، وبعد إعادة الاستثمار يمكن للمرء أن يحصل على نفس المبلغ كما هو الحال عند الاستثمار لمدة عامين بمعدل أعلى. يسمى هذا السعر سعر الفائدة الآجل.لتسهيل حياتك ، دعنا نبسط هذه الصيغة. إذا استخدمنا صيغة حساب الفائدة المستمرة ( FV=PVerT ) ، فيمكننا إعادة كتابة شرط غياب التحكيم على النحو التالي:PVer 2 T 2 = PVer 1 T 1 e (T 2 -T 1 ) xإذا أخذنا اللوغاريتم من كلا الجانبين من المساواة وقمنا بتقليل الثوابت ، نحصل على:r2 T2 = r1 T1 +(T2 -T1)xالتالي ، من السهل العثور على x:x=(r2 T2 - r1 T1 )/(T2 -T1)موافق ، هذه الصيغة لأسعار الفائدة المستقبلية أسهل بكثير وأكثر ملاءمة للاستخدام.يمكنك طرح سؤال - لماذا هذا المنتج الغريب ومن يستخدمه؟تخيل موقفًا ستتلقى فيه أنت أو شركتك أموالًا في غضون عام. ترغب الآن في حماية نفسك من مخاطر التغيرات في أسعار الفائدة. أنت تدرك أنه في عام قد يزيد سعر الفائدة ويصبح أكثر ربحية ، ولكنك أيضًا تفهم أنه يمكن أن ينخفض. وأنت مرتاح للغاية مع سعر الفائدة الآجل الذي يعمل في السوق. ثم يمكنك إبرام عقد ، مشيراً فيه إلى أنه مقابل الأموال التي سيتم استلامها في المستقبل في غضون عام ، فإنك تبرم عقدًا بسعر معين. السعر ثابت ، ولم تعد تقلق بشأن كيفية حدوث التغييرات في أسعار الفائدة في السوق.يرجى ملاحظة أن سعر الفائدة الآجل ليس بأي حال من الأحوال توقعًا للسعر المستقبلي. هذا لا يعني على الإطلاق أن أسعار الفائدة ستكون مساوية لـ 7.7٪ في السنة ، عندما نجد أنفسنا عند النقطة T 1 . يمكنهم أخذ أي قيمة ، ولهذا السبب. في اللحظة التي نحسب فيها سعر الفائدة الآجل من الأسعار المعمول بها في السوق ، يمكننا القول أن هذا السعر هو توقع السوق فيما يتعلق بالأسعار المستقبلية. ولكن بحلول الوقت الذي ننتقل فيه إلى المستقبل ، تحدث أحداث جديدة ، تتم إضافة معلومات جديدة ، ويتغير السوق بطريقة أو بأخرى. لذلك ، لن تتزامن أسعار الفائدة في السنة مع الأسعار الآجلة المحسوبة للسنة الآن.مقالات أخرى في هذه السلسلة :- سندات من الألف إلى الياء ليكبيز لأحد المهوسين ، الجزء 2 (سيتوفر قريبًا)