 في الجزء السابق ، اكتشفنا كيفية عرض كائنات ثنائية الأبعاد ، مثل بكسل وخط (مقطع) ، ولكنك تريد حقًا إنشاء شيء ثلاثي الأبعاد بسرعة. في هذه المقالة ، سنحاول للمرة الأولى عرض كائن ثلاثي الأبعاد على الشاشة والتعرف على كائنات رياضية جديدة ، مثل متجه ومصفوفة ، بالإضافة إلى بعض العمليات عليها ، ولكن فقط تلك التي تنطبق على الممارسة.في الجزء الثاني سننظر في:
في الجزء السابق ، اكتشفنا كيفية عرض كائنات ثنائية الأبعاد ، مثل بكسل وخط (مقطع) ، ولكنك تريد حقًا إنشاء شيء ثلاثي الأبعاد بسرعة. في هذه المقالة ، سنحاول للمرة الأولى عرض كائن ثلاثي الأبعاد على الشاشة والتعرف على كائنات رياضية جديدة ، مثل متجه ومصفوفة ، بالإضافة إلى بعض العمليات عليها ، ولكن فقط تلك التي تنطبق على الممارسة.في الجزء الثاني سننظر في:- نظم الإحداثيات
- النقطة والمتجه
- المصفوفة
- القمم والفهارس
- ناقل التصور
نظم الإحداثيات
تجدر الإشارة إلى أن بعض الأمثلة والعمليات في المقالات يتم تقديمها بشكل غير دقيق ومبسّط بشكل كبير لتحسين فهم المادة ، وإدراك الجوهر ، يمكنك العثور بشكل مستقل على أفضل حل أو إصلاح الأخطاء وعدم الدقة في التعليمات البرمجية التجريبية. قبل أن نرسم شيئًا ثلاثي الأبعاد ، من المهم أن نتذكر أن جميع الأبعاد الثلاثة على الشاشة يتم عرضها بالبكسل ثنائي الأبعاد. من أجل أن تبدو الكائنات المرسومة بالبكسل ثلاثية الأبعاد ، نحتاج إلى إجراء بعض الحسابات الرياضية. لن ننظر في الصيغ والكائنات دون رؤية تطبيقها. هذا هو السبب ، سيتم وضع جميع العمليات الرياضية التي ستواجهها في هذه المقالة موضع التنفيذ ، مما يبسط فهمها. أول شيء يجب فهمه هو نظام الإحداثيات. دعونا نرى ما هي أنظمة الإحداثيات المستخدمة ، وأيضًا اختيار النظام الذي نستخدمه لنا.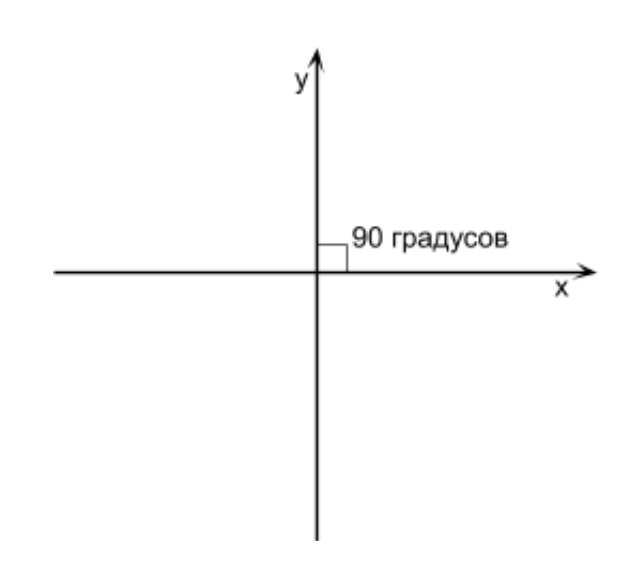 ما هو نظام الإحداثيات؟ هذه طريقة لتحديد موضع نقطة أو شخصية في لعبة تتكون من نقاط باستخدام أرقام. يحتوي نظام الإحداثيات على اتجاهين للمحاور (سنشير إليها على أنها X ، Y) إذا عملنا مع رسومات ثنائية الأبعاد. إذا قمنا بتعيين كائن ثنائي الأبعاد بحجم Y أكبر وأصبح أعلى مما كان عليه من قبل ، فهذا يعني أن المحور Y يكون صعوديًا. إذا أعطينا الكائن X أكبر وأصبح أكثر يمينًا ، فهذا يعني أن المحور X موجه إلى اليمين. هذا هو اتجاه المحاور ، ويطلق عليهم معًا نظام الإحداثيات. إذا تم تشكيل زاوية 90 درجة عند تقاطع محوري X و Y ، فإن نظام الإحداثيات هذا يسمى مستطيل (يسمى أيضًا نظام الإحداثيات الديكارتية) (انظر الشكل أعلاه).
ما هو نظام الإحداثيات؟ هذه طريقة لتحديد موضع نقطة أو شخصية في لعبة تتكون من نقاط باستخدام أرقام. يحتوي نظام الإحداثيات على اتجاهين للمحاور (سنشير إليها على أنها X ، Y) إذا عملنا مع رسومات ثنائية الأبعاد. إذا قمنا بتعيين كائن ثنائي الأبعاد بحجم Y أكبر وأصبح أعلى مما كان عليه من قبل ، فهذا يعني أن المحور Y يكون صعوديًا. إذا أعطينا الكائن X أكبر وأصبح أكثر يمينًا ، فهذا يعني أن المحور X موجه إلى اليمين. هذا هو اتجاه المحاور ، ويطلق عليهم معًا نظام الإحداثيات. إذا تم تشكيل زاوية 90 درجة عند تقاطع محوري X و Y ، فإن نظام الإحداثيات هذا يسمى مستطيل (يسمى أيضًا نظام الإحداثيات الديكارتية) (انظر الشكل أعلاه).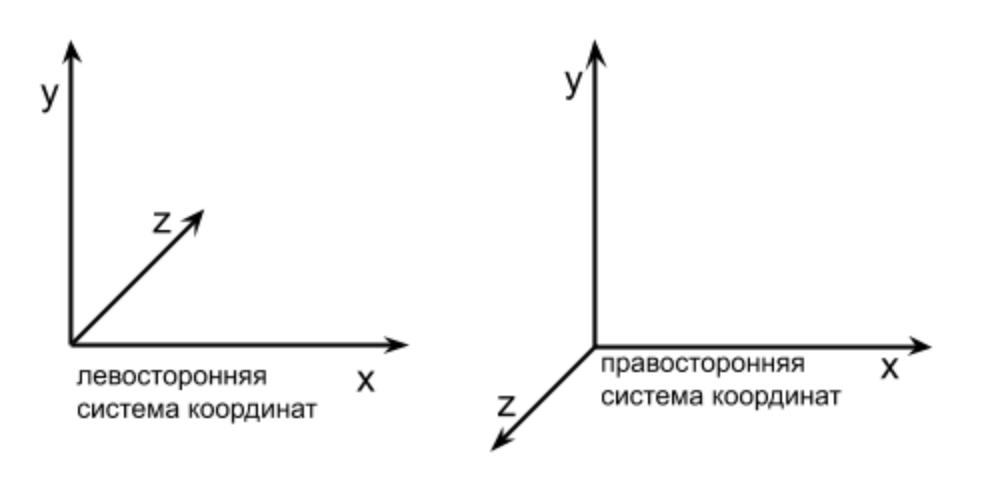
النقطة والمتجه
الآن أنت تعرف ما هي أنظمة الإحداثيات وما هي اتجاهات المحور. بعد ذلك ، تحتاج إلى تحليل ما هي النقطة والمتجه ، لأن سنحتاج إليها في هذه المقالة للممارسة. النقطة في الفضاء ثلاثي الأبعاد هي موقع محدد من خلال [X، Y، Z]. على سبيل المثال ، نريد أن نضع شخصيتنا في الأصل (ربما في وسط النافذة) ، فسيكون موقعه هو [0 ، 0 ، 0] ، أو يمكننا القول أنه موجود في النقطة [0 ، 0 ، 0]. الآن ، نريد وضع الخصم على يسار اللاعب 20 وحدة (على سبيل المثال ، بكسل) ، مما يعني أنه سيكون موجودًا عند النقطة [-20 ، 0 ، 0]. سنعمل باستمرار مع النقاط ، لذلك سنحللها بمزيد من التفصيل لاحقًا. ما هو الناقل؟ هذا هو الاتجاه. في الفضاء ثلاثي الأبعاد ، يتم وصفه ، كنقطة ، بثلاث قيم [X ، Y ، Z]. على سبيل المثال ، نحتاج إلى نقل الحرف لأعلى 5 وحدات كل ثانية ، لذلك سنقوم بتغيير Y ، بإضافة 5 إليه كل ثانية ، لكننا لن نلمس X و Z ، يمكن كتابة هذه الحركة كمتجه [0 ، 5 ، 0]. إذا تحركت شخصيتنا باستمرار إلى أسفل بمقدار وحدتين وإلى اليمين بمقدار 1 ، فإن ناقل حركته سيبدو كما يلي: [1، -2، 0]. كتبنا -2 لأن ينخفض Y إلى أسفل.الناقل ليس له موضع ، وتشير [X ، Y ، Z] إلى الاتجاه. يمكن إضافة ناقل إلى نقطة من أجل الحصول على نقطة جديدة تتحول بواسطة ناقل. على سبيل المثال ، لقد ذكرت بالفعل أعلاه أنه إذا أردنا تحريك كائن ثلاثي الأبعاد (على سبيل المثال ، شخصية لعبة) كل 5 وحدات لأعلى ، فسيكون ناقل الإزاحة على هذا النحو: [0 ، 5 ، 0]. ولكن كيف تستخدمه للتحرك؟ افترض أن الحرف عند النقطة [5 ، 7 ، 0] وأن ناقل الإزاحة هو [0 ، 5 ، 0]. إذا أضفنا متجهًا إلى النقطة ، نحصل على وضع لاعب جديد. يمكنك إضافة نقطة مع متجه ، أو متجه مع متجه وفقًا للقاعدة التالية.مثال على إضافة نقطة و ناقلات :[ 5، 7، 0 ] + [ 0، 5، 0 ] = [ 5 + 0، 7 + 5 ، 0 + 0 ] = [5، 12، 0] - هذا هو الموضع الجديد لشخصيتنا. كما ترون ، تحركت شخصيتنا 5 وحدات لأعلى ، من هنا يظهر مفهوم جديد - طول المتجه. كل متجه لديه ، باستثناء المتجه [0 ، 0 ، 0] ، والذي يسمى المتجه صفر ، مثل هذا المتجه ليس له أيضًا اتجاه. بالنسبة للمتجه [0 ، 5 ، 0] ، الطول هو 5 ، لأنه مثل هذا المتجه يغير النقطة 5 لأعلى. يبلغ طول المتجه [0، 0، 10] 10 لأنه يمكنها تحويل النقطة بمقدار 10 بطول المحور Z ، لكن المتجه [12 ، 3 ، -4] لا يخبرك بالطول ، لذا سنستخدم الصيغة لحساب طول المتجه. السؤال الذي يطرح نفسه ، لماذا نحتاج إلى طول ناقلات؟ أحد التطبيقات هو معرفة إلى أي مدى ستتحرك الشخصية ، أو لمقارنة سرعات الشخصيات التي لديها ناقل إزاحة أطول ، فهذا أسرع. يستخدم الطول أيضًا لبعض العمليات على المتجهات.يمكن حساب طول المتجه باستخدام الصيغة التالية من الجزء الأول (تمت إضافة Z فقط):
دعونا نحسب طول المتجه باستخدام الصيغة أعلاه [6 ، 3 ، -8] ؛
يبلغ طول المتجه [6 ، 3 ، -8] حوالي 10.44.نحن نعلم بالفعل ما هي النقطة ، المتجه ، وكيفية جمع نقطة ومتجه (أو متجهين) ، وكيفية حساب طول المتجه. دعنا نضيف فئة متجهة وننفذ حساب الجمع والطول فيها. أريد أيضًا الانتباه إلى حقيقة أننا لن ننشئ فئة لنقطة ، إذا احتجنا إلى نقطة ، فسوف نستخدم فئة المتجه ، لأن كل من النقطة ومتجر المتجه X ، Y ، Z ، فقط للنقطة في هذا الموضع ، وللناقل الاتجاه.أضف فئة المتجه إلى المشروع من المقالة السابقة ، يمكنك إضافته أسفل فئة الدرج. اتصلت بـ Vector صفي وأضفت 3 خصائص X ، Y ، Z إليها:class Vector {
x = 0;
y = 0;
z = 0;
constructor(x, y, z) {
this.x = x;
this.y = y;
this.z = z;
}
}
لاحظ أن الحقول x ، y ، z بدون وظائف "الموصلات" ، حتى نتمكن من الوصول مباشرة إلى البيانات الموجودة في الكائن ، يتم ذلك للوصول بشكل أسرع. في وقت لاحق ، سنقوم بتحسين هذا الرمز أكثر من ذلك ، ولكن في الوقت الحالي ، نتركه لتحسين القراءة.الآن نقوم بتنفيذ جمع المتجهات. ستستغرق الوظيفة متجهين ملخصين ، لذلك أفكر في جعلها ثابتة. سيعمل نص الوظيفة وفقًا للصيغة أعلاه. نتيجة جمعنا هي ناقل جديد ، سنعود به:static add(v1, v2) {
return new Vector(
v1.x + v2.x,
v1.y + v2.y,
v1.z + v2.z,
);
}
يبقى تنفيذ وظيفة حساب طول المتجه. مرة أخرى ، ننفذ كل شيء وفقًا للصيغ التي كانت أعلى:getLength() {
return Math.sqrt(
this.x * this.x + this.y * this.y + this.z * this.z
);
}
الآن دعونا نلقي نظرة على عملية أخرى على الناقل ، والتي ستكون مطلوبة بعد ذلك بقليل في هذا الموضوع والكثير في المقالات اللاحقة - "تطبيع الناقل". افترض أن لدينا شخصية في اللعبة نتحرك باستخدام مفاتيح الأسهم. إذا ضغطنا لأعلى ، فسينتقل إلى المتجه [0 ، 1 ، 0] ، إذا كان لأسفل ، ثم [0 ، -1 ، 0] ، إلى اليسار [-1 ، 0 ، 0] وإلى اليمين [1 ، 0 ، 0]. يمكن أن نرى بوضوح هنا أن أطوال كل متجهات هي 1 ، أي أن سرعة الشخصية هي 1. ودعنا نضيف حركة قطرية ، إذا قام اللاعب بتثبيت السهم لأعلى وإلى اليمين ، فماذا سيكون ناقل الإزاحة؟ الخيار الأكثر وضوحا هو المتجه [1 ، 1 ، 0]. ولكن إذا حسبنا طوله ، فسوف نرى أنه يساوي تقريبًا 1.414. اتضح أن شخصيتنا سوف تسير بشكل أسرع قطريًا؟ هذا الخيار غير مناسب ، ولكن لكي تسير شخصيتنا بشكل قطري بسرعة 1 ، يجب أن يكون الناقل هو:[0.707 ، 0.707 ، 0]. من أين حصلت على مثل هذا الناقل؟ أخذت المتجه [1 ، 1 ، 0] وقمت بتطبيعته ، وبعد ذلك حصلت على [0.707 ، 0.707 ، 0]. بمعنى ، التطبيع هو تقليل المتجه إلى طول 1 (طول الوحدة) دون تغيير اتجاهه. لاحظ أن المتجهات [0.707 ، 0.707 ، 0] و [1 ، 1 ، 0] تشير في نفس الاتجاه ، أي أن الحرف سوف يتحرك في كلتا الحالتين بدقة إلى اليمين ، ولكن المتجه [0.707 ، 0.707 ، 0] يتم تطبيعه وسرعة الحرف الآن ستكون مساوية لـ 1 ، مما يزيل الخلل بحركة قطرية متسارعة. يوصى دائمًا بتطبيع المتجه قبل أي حسابات لتجنب أنواع مختلفة من الأخطاء. دعونا نرى كيفية تطبيع ناقلات. من الضروري تقسيم كل من مكوناته (X ، Y ، Z) على طوله. وظيفة إيجاد الطول موجودة بالفعل ، تم إنجاز نصف العمل ،الآن نكتب دالة تطبيع المتجه (داخل فئة المتجه):normalize() {
const length = this.getLength();
this.x /= length;
this.y /= length;
this.z /= length;
return this;
}
تعمل طريقة التطبيع على تطبيع المتجه وإعادته (هذا) ، وهذا ضروري حتى يكون من الممكن في المستقبل استخدام التطبيع في التعبيرات.الآن بعد أن عرفنا ما هو تطبيع ناقل ، ونعلم أنه من الأفضل القيام به قبل استخدام الناقل ، يطرح السؤال. إذا كان تطبيع المتجه هو تقليل إلى طول الوحدة ، أي أن سرعة حركة الجسم (الحرف) ستكون مساوية 1 ، فكيف تسريع الشخصية؟ على سبيل المثال ، عند تحريك شخصية قطريًا لأعلى / لليمين بسرعة 1 ، سيكون متجهه [0.707 ، 0.707 ، 0] ، وما هو المتجه إذا أردنا تحريك الشخصية أسرع 6 مرات؟ للقيام بذلك ، هناك عملية تسمى "ضرب متجه بمقياس." العدد هو العدد المعتاد الذي يتم فيه ضرب المتجه. إذا كان العدد يساوي 6 ، فسيصبح المتجه أطول 6 مرات ، وشخصيتنا أسرع 6 مرات ، على التوالي. كيف يتم الضرب العددي؟ لهذا ، من الضروري مضاعفة كل مكون للمتجه في العدد. على سبيل المثال ، نحل المشكلة أعلاه ،عندما يحتاج حرف ينتقل إلى متجه [0.707 ، 0.707 ، 0] (السرعة 1) إلى التسريع 6 مرات ، أي ضرب المتجه في العدد 6. صيغة ضرب المتجه "V" في العدد "s" هي كما يلي:
في حالتنا ، سيكون:- متجه إزاحة جديد يبلغ طوله 6. منالمهم معرفة أن العدد الإيجابي يقيس متجهًا دون تغيير اتجاهه ؛ إذا كان العدد سلبيًا ، فإنه يقيس أيضًا متجهًا (يزيد طوله) ولكن بالإضافة إلى ذلك يغير اتجاه المتجه إلى العكس.دعونا ننفذ وظيفة multiplyByScalarضرب متجه بمقياس في فئة المتجه الخاصة بنا:multiplyByScalar(s) {
this.x *= s;
this.y *= s;
this.z *= s;
return this;
}
المصفوفة
اكتشفنا قليلاً مع المتجهات وبعض العمليات عليها التي ستكون مطلوبة في هذه المقالة. بعد ذلك ، تحتاج إلى التعامل مع المصفوفات.يمكننا أن نقول أن المصفوفة هي الصفيف ثنائي الأبعاد الأكثر شيوعًا. إنه فقط في البرمجة يستخدمون مصطلح "صفيف ثنائي الأبعاد" ، وفي الرياضيات يستخدمون "المصفوفة". لماذا المصفوفات مطلوبة في البرمجة ثلاثية الأبعاد؟ سنحلل هذا بمجرد أن نتعلم العمل معهم قليلاً. سنستخدم المصفوفات العددية فقط (مجموعة من الأرقام). كل مصفوفة لها حجمها الخاص (مثل أي مصفوفة ثنائية الأبعاد). فيما يلي بعض الأمثلة على المصفوفات:من بين جميع عمليات المصفوفات ، نعتبر الآن الضرب فقط (الباقي لاحقًا). اتضح أن ضرب المصفوفة ليس أسهل عملية ، يمكن أن يخلط بسهولة إذا لم تتبع ترتيب الضرب بعناية. ولكن لا تقلق ، ستنجح ، لأنه هنا سنقوم فقط بالضرب والتلخيص. بادئ ذي بدء ، نحتاج إلى تذكر بعض ميزات الضرب التي نحتاجها:- إذا حاولنا ضرب الرقم A في الرقم B ، فهذا هو نفس B * A. إذا أعدنا ترتيب المعاملات ولم تتغير النتيجة تحت أي إجراء ، فإنهم يقولون أن العملية تبادلية. مثال: أ + ب = ب + أ العملية تبادلية ، أ - ب- ب - أ العملية غير تبادلية ، أ * ب = ب * أ عملية ضرب الأعداد تبادلية. لذا ، فإن عملية ضرب المصفوفة غير تبادلية ، على النقيض من ضرب الأرقام. أي أن ضرب المصفوفة M في المصفوفة N لن يساوي ضرب المصفوفة N في M.
- يمكن مضاعفة المصفوفة إذا كان عدد أعمدة المصفوفة الأولى (الموجودة على اليسار) يساوي عدد الصفوف في المصفوفة الثانية (التي على اليمين).
سنلقي الآن نظرة على الميزة الثانية لضرب المصفوفة (عندما يكون الضرب ممكنًا). فيما يلي بعض الأمثلة التي توضح متى يكون الضرب ممكنًا وعندما لا يكون:أعتقد أن هذه الأمثلة أوضحت الصورة قليلاً عندما يكون الضرب ممكنًا. ستكون نتيجة ضرب المصفوفة دائمًا مصفوفة ، وعدد الصفوف التي تساوي عدد صفوف المصفوفة الأولى ، وعدد الأعمدة يساوي عدد أعمدة المصفوفة الثانية. على سبيل المثال ، إذا قمنا بضرب المصفوفة 2 في 6 و 6 في 8 ، نحصل على مصفوفة من الحجم 2 في 8. والآن ننتقل مباشرة إلى الضرب نفسه.من أجل الضرب ، من المهم أن نتذكر أن الأعمدة والصفوف في المصفوفة مرقمة بدءًا من 1 ، وفي المصفوفة من 0. يشير الفهرس الأول في عنصر المصفوفة إلى رقم الصف ، والثاني رقم العمود. بمعنى ، إذا تمت كتابة عنصر المصفوفة (عنصر الصفيف) على النحو التالي: m28 ، فهذا يعني أننا ننتقل إلى الصف الثاني والعمود الثامن. ولكن نظرًا لأننا سنعمل مع المصفوفات في الشفرة ، فستبدأ جميع فهرسة الصفوف والأعمدة عند 0.دعونا نحاول ضرب مصفوفتين A و B بأحجام وعناصر محددة:
يمكن ملاحظة أن المصفوفة A لها حجم 3 × 2 ، والمصفوفة B لها حجم 2 × 2 ، الضرب ممكن:
كما ترى ، لدينا مصفوفة 3 في 2 ، الضرب مربك في البداية ، ولكن إذا كان هناك هدف لتعلم كيفية الضرب "بدون ضغط" ، فيجب حل عدة أمثلة. هنا مثال آخر لضرب المصفوفات A و B:
إذا لم يكن الضرب واضحًا تمامًا ، فلا بأس ، لأنه لا يجب أن نضرب بالأوراق. سنكتب بمجرد دالة ضرب المصفوفة وسنستخدمها. بشكل عام ، كل هذه الوظائف مكتوبة بالفعل ، لكننا نفعل كل شيء بمفردنا.الآن بعض المصطلحات الأخرى التي سيتم استخدامها في المستقبل:- المصفوفة المربعة هي مصفوفة يكون فيها عدد الصفوف مساويًا لعدد الأعمدة ، وهنا مثال للمصفوفات المربعة:
- يسمى القطر الرئيسي للمصفوفة المربعة جميع عناصر المصفوفة التي يساوي رقم صفها رقم العمود. أمثلة على الأقطار (في هذا المثال ، يمتلئ القطر الرئيسي بتسعة):
- مصفوفة الوحدة هي مصفوفة مربعة تكون فيها جميع عناصر القطر الرئيسي 1 وجميع العناصر الأخرى 0. أمثلة لمصفوفات الوحدة:
من المهم أيضًا تذكر هذه الخاصية أنه إذا قمنا بضرب أي مصفوفة M في مصفوفة وحدة مناسبة في الحجم ، على سبيل المثال ، نسميها I ، نحصل على المصفوفة الأصلية M ، على سبيل المثال: M * I = M أو I * M = M. لا يؤثر ضرب المصفوفة في مصفوفة الهوية على النتيجة. سنعود إلى مصفوفة الهوية لاحقًا. في البرمجة ثلاثية الأبعاد ، سنستخدم غالبًا مصفوفة مربعة 4 × 4.الآن دعونا نلقي نظرة على سبب حاجتنا للمصفوفات ولماذا نضربها؟ في البرمجة ثلاثية الأبعاد ، هناك العديد من المصفوفات 4 × 4 المختلفة التي ، إذا تم ضربها في متجه أو نقطة ، ستقوم بالإجراءات التي نحتاجها. على سبيل المثال ، نحتاج إلى تدوير الحرف في مساحة ثلاثية الأبعاد حول المحور X ، كيف نفعل ذلك؟ اضرب المتجه في مصفوفة خاصة ، تكون مسؤولة عن التدوير حول المحور X. إذا كنت بحاجة إلى تحريك وتدوير نقطة حول الأصل ، فأنت بحاجة إلى ضرب هذه النقطة في مصفوفة خاصة. المصفوفات لها خاصية ممتازة - الجمع بين التحولات (سننظر في هذه المقالة). لنفترض أننا نحتاج إلى حرف يتكون من 100 نقطة (القمم ، ولكن هذا سيكون أيضًا أقل قليلاً) في التطبيق ، قم بزيادة 5 مرات ، ثم قم بتدوير 90 درجة X ، ثم حركه لأعلى 30 وحدة.كما ذكرنا سابقًا ، بالنسبة إلى الإجراءات المختلفة ، هناك بالفعل مصفوفات خاصة سننظر فيها. لإنجاز المهمة المذكورة أعلاه ، فإننا ، على سبيل المثال ، ندور في كل 100 نقطة وكل نقطة نضربها في المصفوفة الأولى لزيادة الشخصية ، ثم نضرب في المصفوفة الثانية لتدوير 90 درجة في X ، ثم نضرب في 3 عشر لنقل 30 وحدة للأعلى. إجمالاً ، لكل نقطة لدينا 3 مضاعفات مصفوفة ، و 100 نقطة ، مما يعني أنه سيكون هناك 300 مضاعف. ولكن إذا أخذنا المصفوفات وضاعفناها بيننا لزيادة 5 مرات ، فقم بتدوير 90 درجة على طول X والتحرك بمقدار 30 وحدة. يصل ، نحصل على مصفوفة تحتوي على كل هذه الإجراءات. بضرب نقطة في هذه المصفوفة ، ستكون النقطة حيث هناك حاجة إليها. الآن دعونا نحسب عدد الإجراءات التي يتم تنفيذها: مضاعفتان لـ 3 مصفوفات ، و 100 عملية ضرب لـ 100 نقطة ،ما مجموعه 102 مضاعفات أفضل بالتأكيد من 300 مضاعف قبل ذلك. اللحظة التي قمنا فيها بضرب 3 مصفوفات لدمج الإجراءات المختلفة في مصفوفة واحدة - تسمى مجموعة من التحولات وسنفعلها بالتأكيد بمثال.درسنا كيفية ضرب المصفوفة في المصفوفة ، ولكن قراءة الفقرة أعلاه تتحدث عن ضرب المصفوفة بنقطة أو متجه. لمضاعفة نقطة أو متجه ، يكفي تمثيلها كمصفوفة.على سبيل المثال ، لدينا متجه [10 ، 2 ، 5] وهناك مصفوفة:
يمكن ملاحظة أن المتجه يمكن تمثيله بمصفوفة 1 × 3 أو مصفوفة 3 × 1. لذلك ، يمكننا ضرب المتجه بمصفوفة بطريقتين:كما ترى ، يمكننا تمثيل المتجه كمتجه صف وضربه في مصفوفة ، أو تمثيل المتجه كمتجه عمود وضرب المصفوفة به. دعونا نتحقق مما إذا كانت نتيجة الضرب ستكون هي نفسها في كلتا الحالتين:اضرب متجه الصف في المصفوفة:
الآن ، اضرب المصفوفة في متجه العمود:
نرى أن ضرب متجه الصف في المصفوفة والمصفوفة في متجه العمود ، حصلنا على نتائج مختلفة تمامًا (نتذكر التبادلية). لذلك ، في البرمجة الثلاثية الأبعاد ، توجد مصفوفات مصممة ليتم ضربها في متجه صف فقط ، أو في متجه عمود فقط. إذا قمنا بضرب المصفوفة المخصصة لمتجه الصف في متجه العمود ، نحصل على نتيجة لن تعطينا أي شيء. استخدم تمثيل المتجه / النقطة المناسب لك (الصف أو العمود) ، فقط في المستقبل ، استخدم المصفوفات المناسبة لتمثيل المتجه / النقطة. يستخدم Direct3D ، على سبيل المثال ، تمثيل سلسلة من المتجهات ، وتم تصميم جميع المصفوفات في Direct3D لضرب متجه الصف في المصفوفة. يستخدم OpenGL تمثيل متجه (أو نقطة) كعمود ،وقد تم تصميم جميع المصفوفات لضرب المصفوفة في متجه عمود. في المقالات سنستخدم متجه العمود وسنقوم بضرب المصفوفة في متجه العمود.لتلخيص ما نقرأه عن المصفوفة.- لتنفيذ إجراء على ناقل (أو نقطة) ، هناك مصفوفات خاصة ، سنرى بعضها في هذه المقالة.
- لدمج التحويل (الإزاحة ، الدوران ، إلخ) ، يمكننا مضاعفة مصفوفات كل تحويل مع بعضها البعض والحصول على مصفوفة تحتوي على جميع التحولات معًا.
- في البرمجة ثلاثية الأبعاد ، سنستخدم باستمرار مصفوفات مربعة 4 × 4.
- يمكننا ضرب المصفوفة بموجه (أو نقطة) من خلال تمثيلها كعمود أو صف. ولكن بالنسبة لمتجه العمود ومتجه الصف ، تحتاج إلى استخدام مصفوفات مختلفة.
بعد تحليل بسيط للمصفوفات ، دعنا نضيف فئة مصفوفة 4 × 4 ونطبق طرق لضرب المصفوفة بالمصفوفة ، والمتجه بالمصفوفة. سنستخدم حجم المصفوفة 4 × 4 ، لأن جميع المصفوفات القياسية المستخدمة في الإجراءات المختلفة (الحركة ، الدوران ، المقياس ، ...) هي من هذا الحجم ، لا نحتاج إلى مصفوفات ذات حجم مختلف. دعنا نضيف فئة Matrix إلى المشروع. لا يزال أحيانًا يسمى الفصل الدراسي للعمل مع مصفوفات 4 × 4 Matrix4 ، ويخبرنا هذا 4 في العنوان عن حجم المصفوفة (يقولون أيضًا مصفوفة الترتيب الرابع). سيتم تخزين جميع بيانات المصفوفة في صفيف ثنائي الأبعاد 4 × 4.ننتقل إلى تنفيذ عمليات الضرب. لا أوصي باستخدام حلقات لهذا. لتحسين الأداء ، يتعين علينا جميعًا مضاعفة سطرًا تلو الآخر - سيحدث هذا نظرًا لحقيقة أن جميع المضاعفات ستحدث مع مصفوفات ذات حجم ثابت. سأستخدم دورات لعملية الضرب ، فقط لحفظ كمية التعليمات البرمجية ، يمكنك كتابة جميع عمليات الضرب بدون دورات على الإطلاق. كود الضرب الخاص بي يبدو كالتالي:class Matrix {
static multiply(a, b) {
const m = [
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
];
for (let i = 0; i < 4; i++) {
for (let j = 0; j < 4; j++) {
m[i][j] = a[i][0] * b[0][j] +
a[i][1] * b[1][j] +
a[i][2] * b[2][j] +
a[i][3] * b[3][j];
}
}
return m;
}
}
كما ترون ، تأخذ الطريقة المصفوفات a و b ، وتضربهم وتعيد النتيجة في نفس المصفوفة 4 في 4. في بداية الطريقة قمت بإنشاء مصفوفة m مليئة بالأصفار ، لكن هذا ليس ضروريًا ، لذلك أردت أن أري الأبعاد التي ستكون النتيجة ، أنت يمكنك إنشاء صفيف 4 × 4 بدون أي بيانات.الآن تحتاج إلى تنفيذ عملية ضرب المصفوفة بواسطة متجه العمود ، كما هو موضح أعلاه. ولكن إذا كنت تمثل المتجه كعمود ، فستحصل على مصفوفة من النموذج:الذي سنحتاج من خلاله إلى الضرب في 4 في 4 مصفوفات لأداء إجراءات مختلفة. ولكن في هذا المثال ، يُلاحظ بوضوح أنه لا يمكن إجراء مثل هذا الضرب ، لأن ناقل العمود يحتوي على 3 صفوف ، وللمصفوفة 4 أعمدة. ثم ماذا تفعل؟ هناك حاجة إلى بعض العناصر الرابعة ، ثم سيكون للمتجه 4 صفوف ، والتي ستكون مساوية لعدد الأعمدة في المصفوفة. دعنا نضيف معلمة رابعة إلى المتجه ونطلق عليه W ، والآن لدينا جميع المتجهات ثلاثية الأبعاد للنموذج [X ، Y ، Z ، W] ويمكن ضرب هذه المتجهات بالفعل في المصفوفة 4 في 4. في الواقع ، المكون W غرض أعمق ، لكننا سنتعرف عليه في الجزء التالي (ليس من أجل لا شيء لدينا مصفوفة 4 × 4 ، وليس مصفوفة 3 × 3). أضف إلى فئة Vector ، التي أنشأناها فوق المكون w. الآن تبدو بداية فئة Vector كما يلي:class Vector {
x = 0;
y = 0;
z = 0;
w = 1;
constructor(x, y, z, w = 1) {
this.x = x;
this.y = y;
this.z = z;
this.w = w;
}
لقد قمت بتهيئة W إلى واحد ، ولكن لماذا 1؟ إذا نظرنا إلى كيفية مضاعفة مكونات المصفوفة والمتجه (مثال الرمز أدناه) ، يمكنك أن ترى أنه إذا قمت بتعيين W إلى 0 أو أي قيمة أخرى غير 1 ، فعند ضرب هذا W سيؤثر على النتيجة ، لكننا لا نحن نعرف كيفية استخدامه ، وإذا قمنا بعمله 1 ، فسيكون في المتجه ، ولكن النتيجة لن تتغير بأي شكل من الأشكال. الآن نعود إلى المصفوفة وتنفيذها في فئة المصفوفة (يمكنك أيضًا في فئة المتجهات ، لا يوجد فرق) المصفوفة مضروبة في متجه ، وهو ممكن بالفعل ، بفضل W:static multiplyVector(m, v) {
return new Vector(
m[0][0] * v.x + m[0][1] * v.y + m[0][2] * v.z + m[0][3] * v.w,
m[1][0] * v.x + m[1][1] * v.y + m[1][2] * v.z + m[1][3] * v.w,
m[2][0] * v.x + m[2][1] * v.y + m[2][2] * v.z + m[2][3] * v.w,
m[3][0] * v.x + m[3][1] * v.y + m[3][2] * v.z + m[3][3] * v.w,
)
}
يرجى ملاحظة أننا قدمنا المصفوفة كمصفوفة 4 × 4 ، والمتجه ككائن له الخصائص x ، y ، z ، w ، في المستقبل سنقوم بتغيير المتجه وسيتم تمثيله أيضًا بمصفوفة 1 × 4 ، لأنه سوف تسريع عملية الضرب. ولكن الآن ، من أجل رؤية أفضل لكيفية حدوث الضرب وتحسين فهم الشفرة ، لن نقوم بتغيير المتجه.قمنا بكتابة كود ضرب المصفوفة فيما بيننا وضرب المصفوفات المتجهية ، ولكن لا يزال من غير الواضح كيف سيساعدنا ذلك في الرسومات ثلاثية الأبعاد.أريد أيضًا أن أذكرك بأنني أسمي المتجه بنقطة (موضع في الفضاء) واتجاه ، لأن يحتوي كلا الكائنين على نفس بنية البيانات x و y و z و w التي تم تقديمها حديثًا. دعونا نلقي نظرة على بعض المصفوفات التي تؤدي العمليات الأساسية على المتجهات. وستكون مصفوفة الترجمة الأولى من هذه المصفوفات. بضرب مصفوفة الإزاحة بواسطة متجه (موقع) ، فإنها ستتحول بعدد محدد من الوحدات في الفضاء. وهنا مصفوفة الإزاحة:
حيث تعني dx و dy و dz الإزاحة على طول المحاور x و y و z على التوالي ، فقد تم تصميم هذه المصفوفة ليتم ضربها في متجه عمود. يمكن العثور على هذه المصفوفات على الإنترنت أو في أي أدب عن البرمجة ثلاثية الأبعاد ، لا نحتاج إلى إنشائها بأنفسنا ، خذها الآن ، مثل الصيغ التي تستخدمها من المدرسة التي تحتاج فقط إلى معرفتها أو فهم سبب استخدامها. دعونا نتحقق مما إذا كان ضرب هذه المصفوفة في الواقع متجهًا ، فسيحدث الإزاحة. خذ كمتجه سنقوم بتحريك المتجه [10 ، 10 ، 10 ، 1] (نترك دائمًا المعلمة الرابعة W دائمًا 1) ، لنفترض أن هذا هو موقف شخصيتنا في اللعبة ونريد نقله 10 وحدات لأعلى ، 5 وحدات على اليمين ، وعلى بعد وحدة واحدة من الشاشة. ثم سيكون ناقل الإزاحة على هذا النحو [10 ، 5 ، -1] (-1 لأن لدينا نظام إحداثيات يمينًا و Z إضافي ،أصغر هو). إذا قمنا بحساب النتيجة بدون مصفوفات ، عن طريق الجمع المعتاد للمتجهات. سيؤدي ذلك إلى النتيجة التالية: [10 + 10 ، 10 + 5 ، 10 + -1 ، 1] = [20 ، 15 ، 9 ، 1] - هذه هي الإحداثيات الجديدة لشخصيتنا. بضرب المصفوفة أعلاه بالإحداثيات الأولية [10 ، 10 ، 10 ، 1] ، يجب أن نحصل على نفس النتيجة ، دعنا نتحقق من ذلك في الكود ، نكتب الضرب بعد فئات الدرج ، المتجه والمصفوفة:const translationMatrix = [
[1, 0, 0, 10],
[0, 1, 0, 5],
[0, 0, 1, -1],
[0, 0, 0, 1],
]
const characterPosition = new Vector(10, 10, 10)
const newCharacterPosition = Matrix.multiplyVector(
translationMatrix, characterPosition
)
console.log(newCharacterPosition)
في هذا المثال ، استبدلنا إزاحة الحرف المطلوبة (translationMatrix) في مصفوفة الإزاحة ، وقمنا بتهيئة موضعها الأولي (CharacterPosition) ثم قمنا بضربه في المصفوفة ، وكانت النتيجة هي الإخراج عبر console.log (هذا هو إخراج التصحيح في JS). إذا كنت تستخدم لغة ليست JS ، فقم بإخراج X و Y و Z بنفسك باستخدام أدوات لغتك. النتيجة التي حصلنا عليها في وحدة التحكم: [20 ، 15 ، 9 ، 1] ، كل شيء يتفق مع النتيجة التي حسبناها أعلاه. قد يكون لديك سؤال ، لماذا تحصل على نفس النتيجة عن طريق ضرب المتجه في مصفوفة خاصة ، إذا حصلنا عليه أسهل بكثير عن طريق جمع المتجه بمقابل تعويض. الجواب ليس أبسط وسنناقشه بمزيد من التفصيل ، ولكن الآن يمكننا أن نلاحظ أنه ، كما تمت مناقشته سابقًا ، يمكننا دمج المصفوفات مع التحولات المختلفة فيما بينها ،وبالتالي تقليص العديد من الحسابات. في المثال أعلاه ، أنشأنا مصفوفة translationMatrix يدويًا واستبدلنا الإزاحة اللازمة هناك ، ولكن نظرًا لأننا غالبًا ما نستخدم هذه المصفوفات والمصفوفات الأخرى ، فلنضعها في طريقة في فئة Matrix وننقل الإزاحة إليها بالحجج:static getTranslation(dx, dy, dz) {
return [
[1, 0, 0, dx],
[0, 1, 0, dy],
[0, 0, 1, dz],
[0, 0, 0, 1],
]
}
ألق نظرة عن كثب على مصفوفة الإزاحة ، سترى أن dx ، dy ، dz موجودة في العمود الأخير وإذا نظرنا إلى رمز ضرب المصفوفة بواسطة متجه ، فسوف نلاحظ أن هذا العمود مضروب في المكون W للمتجه. وإذا كانت ، على سبيل المثال ، 0 ، ثم dx ، dy ، dz ، فسنضرب في 0 ولن تعمل الخطوة. لكن يمكننا أن نفعل W يساوي 0 إذا أردنا تخزين الاتجاه في فئة Vector ، لأن من المستحيل تحريك الاتجاه ، لذا فإننا نحمي أنفسنا ، وحتى إذا قمنا بمضاعفة مثل هذا الاتجاه في مصفوفة الإزاحة ، فإن هذا لن يكسر اتجاه الاتجاه ، لأنه سيتم ضرب كل حركة في 0.المجموع يمكننا تطبيق مثل هذه القاعدة ، نقوم بإنشاء موقع مثل هذا:new Vector(x, y, z, 1)
وسنقوم بإنشاء الاتجاه مثل هذا:new Vector(x, y, z, 0)
حتى نتمكن من التمييز بين الموقع والاتجاه ، وعندما نضرب الاتجاه في مصفوفة الإزاحة ، فإننا لا نكسر متجه الاتجاه عن طريق الخطأ.القمم والفهارس
قبل أن نرى ما هي المصفوفات الأخرى ، سننظر قليلاً في كيفية تطبيق معرفتنا الحالية لعرض شيء ثلاثي الأبعاد على الشاشة. كل ما استخلصناه قبل ذلك هو الخطوط والبكسل. لكن دعونا الآن نستخدم هذه الأدوات لاشتقاق ، على سبيل المثال ، مكعب. من أجل القيام بذلك ، نحتاج إلى معرفة ما يتكون نموذج ثلاثي الأبعاد. العنصر الأساسي في أي نموذج ثلاثي الأبعاد هو النقاط (سنطلق عليها الرؤوس أدناه) التي يمكننا رسمها على طولها ؛ هذه ، في الواقع ، الكثير من نواقل الموقع ، والتي إذا ربطناها بشكل صحيح مع الخطوط ، نحصل على نموذج ثلاثي الأبعاد (شبكة النموذج ) على الشاشة ، سيكون بدون نسيج وبدون العديد من الخصائص الأخرى ، ولكن كل شيء له وقته. ألق نظرة على المكعب الذي نريد إخراجه وحاول فهم عدد القمم التي يحتوي عليها: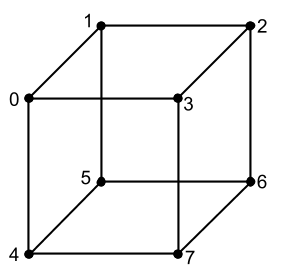
const vertices = [
new Vector(-1, 1, 1),
new Vector(-1, 1, -1),
new Vector(1, 1, -1),
new Vector(1, 1, 1),
new Vector(-1, -1, 1),
new Vector(-1, -1, -1),
new Vector(1, -1, -1),
new Vector(1, -1, 1),
];
أضع كل قمة في مثيل لفئة Vector ، وهذا ليس أفضل خيار للأداء (أفضل في مصفوفة) ، ولكن هدفنا الآن هو معرفة كيفية عمل كل شيء.لنأخذ الآن إحداثيات رؤوس المكعب على شكل وحدات بكسل سنرسمها على الشاشة ، في هذه الحالة نرى أن حجم المكعب 2 × 2 × 2 بكسل. لقد أنشأنا مثل هذا المكعب الصغير بحيث ننظر إلى عمل مصفوفة التحجيم ، والتي سنزيد بها. في المستقبل ، من الممارسات الجيدة جدًا جعل النماذج صغيرة ، حتى أصغر من نماذجنا ، من أجل زيادتها إلى الحجم المطلوب بدون مقاييس مختلفة تمامًا.الأمر فقط أن رسم نقاط المكعب بالبكسل ليس واضحًا جدًا ، لأنه كل ما سنراه هو 8 بكسل ، واحدة لكل قمة ، من الأفضل بكثير رسم مكعب مع خطوط باستخدام وظيفة drawLine من المقالة السابقة. لكن من أجل هذا نحتاج أن نفهم من أي القمم التي نمر إليها الخطوط. ألق نظرة على صورة المكعب مع المؤشرات مرة أخرى وسنرى أنها تتكون من 12 خطًا (أو حوافًا). من السهل أيضًا رؤية أننا نعرف إحداثيات بداية ونهاية كل سطر. على سبيل المثال ، يجب رسم أحد الخطوط (الجزء العلوي القريب) من القمة 0 إلى القمة 3 ، أو من الإحداثيات [-1 ، 1 ، 1] إلى الإحداثيات [1 ، 1 ، 1]. سيتعين علينا كتابة معلومات حول كل سطر في الكود بالنظر يدويًا إلى صورة المكعب ، ولكن كيف نفعل ذلك بشكل صحيح؟ إذا كان لدينا 12 سطرًا وكان لكل سطر بداية ونهاية ، أي نقطتين ، إذن ،لرسم مكعب نحتاج 24 نقطة؟ هذه هي الإجابة الصحيحة ، ولكن دعنا نلقي نظرة على صورة المكعب مرة أخرى وننتبه إلى حقيقة أن كل سطر في المكعب يحتوي على رؤوس مشتركة ، على سبيل المثال ، في الرأس 0 3 خطوط متصلة ، وهكذا مع كل قمة. يمكننا حفظ الذاكرة وعدم كتابة إحداثيات بداية ونهاية كل سطر ، فقط قم بإنشاء مصفوفة وحدد مؤشرات قمة الرأس من مصفوفة الذروة التي تبدأ فيها هذه الخطوط وتنتهي. دعونا ننشئ مثل هذا المصفوفة ونصفها فقط بمؤشرات القمة ، 2 فهرس لكل سطر (بداية السطر والنهاية). وأكثر قليلاً ، عندما نرسم هذه الخطوط ، يمكننا بسهولة الحصول على إحداثياتهم من مجموعة القمم. مجموعتي من الخطوط (أسميتها حواف ، لأن هذه هي حواف المكعب) لقد أنشأت مصفوفة من القمم أدناه وتبدو على النحو التالي:ولكن دعونا نلقي نظرة على صورة المكعب مرة أخرى وننتبه إلى حقيقة أن كل سطر من المكعب يحتوي على رؤوس مشتركة ، على سبيل المثال ، في vertex 0 3 خطوط متصلة ، وهكذا مع كل قمة. يمكننا حفظ الذاكرة وعدم كتابة إحداثيات بداية ونهاية كل سطر ، فقط قم بإنشاء مصفوفة وحدد مؤشرات قمة الرأس من مصفوفة الذروة التي تبدأ فيها هذه الخطوط وتنتهي. دعونا ننشئ مثل هذا المصفوفة ونصفها فقط بمؤشرات القمة ، 2 فهرس لكل سطر (بداية السطر والنهاية). وأكثر قليلاً ، عندما نرسم هذه الخطوط ، يمكننا بسهولة الحصول على إحداثياتهم من مجموعة القمم. مجموعتي من الخطوط (أسميتها حواف ، لأن هذه هي حواف المكعب) لقد أنشأت مصفوفة من القمم أدناه وتبدو على النحو التالي:ولكن دعونا نلقي نظرة على صورة المكعب مرة أخرى وننتبه إلى حقيقة أن كل سطر من المكعب يحتوي على رؤوس مشتركة ، على سبيل المثال ، في vertex 0 3 خطوط متصلة ، وهكذا مع كل قمة. يمكننا حفظ الذاكرة وعدم كتابة إحداثيات بداية ونهاية كل سطر ، فقط قم بإنشاء مصفوفة وحدد مؤشرات قمة الرأس من مصفوفة الذروة التي تبدأ فيها هذه الخطوط وتنتهي. دعونا ننشئ مثل هذا المصفوفة ونصفها فقط بمؤشرات القمة ، 2 فهرس لكل سطر (بداية السطر والنهاية). وأكثر قليلاً ، عندما نرسم هذه الخطوط ، يمكننا بسهولة الحصول على إحداثياتهم من مجموعة القمم. مجموعتي من الخطوط (أسميتها حواف ، لأن هذه هي حواف المكعب) لقد أنشأت مصفوفة من القمم أدناه وتبدو على النحو التالي:وهكذا مع كل قمة. يمكننا حفظ الذاكرة وعدم كتابة إحداثيات بداية ونهاية كل سطر ، فقط قم بإنشاء مصفوفة وحدد مؤشرات قمة الرأس من مصفوفة الذروة التي تبدأ فيها هذه الخطوط وتنتهي. دعونا ننشئ مثل هذا المصفوفة ونصفها فقط بمؤشرات القمة ، 2 فهرس لكل سطر (بداية السطر والنهاية). وأكثر قليلاً ، عندما نرسم هذه الخطوط ، يمكننا بسهولة الحصول على إحداثياتهم من مجموعة القمم. مجموعتي من الخطوط (أسميتها حواف ، لأن هذه هي حواف المكعب) لقد أنشأت مصفوفة من القمم أدناه وتبدو على النحو التالي:وهكذا مع كل قمة. يمكننا حفظ الذاكرة وعدم كتابة إحداثيات بداية ونهاية كل سطر ، فقط قم بإنشاء مصفوفة وحدد مؤشرات قمة الرأس من مصفوفة الذروة التي تبدأ فيها هذه الخطوط وتنتهي. دعونا ننشئ مثل هذا المصفوفة ونصفها فقط بمؤشرات القمة ، 2 فهرس لكل سطر (بداية السطر والنهاية). وأكثر قليلاً ، عندما نرسم هذه الخطوط ، يمكننا بسهولة الحصول على إحداثياتهم من مجموعة القمم. مجموعتي من الخطوط (أسميتها حواف ، لأن هذه هي حواف المكعب) لقد أنشأت مصفوفة من القمم أدناه وتبدو على النحو التالي:2 فهرس في كل سطر (بداية السطر ونهايته). وأكثر قليلاً ، عندما نرسم هذه الخطوط ، يمكننا بسهولة الحصول على إحداثياتهم من مجموعة القمم. مجموعتي من الخطوط (أسميتها حواف ، لأن هذه هي حواف المكعب) لقد أنشأت مصفوفة من القمم أدناه وتبدو على النحو التالي:2 فهرس في كل سطر (بداية السطر ونهايته). وأكثر قليلاً ، عندما نرسم هذه الخطوط ، يمكننا بسهولة الحصول على إحداثياتهم من مجموعة القمم. مجموعتي من الخطوط (أسميتها حواف ، لأن هذه هي حواف المكعب) لقد أنشأت مصفوفة من القمم أدناه وتبدو على النحو التالي:
const edges = [
[0, 1],
[1, 2],
[2, 3],
[3, 0],
[0, 4],
[1, 5],
[2, 6],
[3, 7],
[4, 5],
[5, 6],
[6, 7],
[7, 4],
];
يوجد 12 زوجا من المؤشرات في هذا الصفيف ، 2 مؤشر قمة في كل سطر.دعونا نتعرف على مصفوفة أخرى من شأنها زيادة المكعب الخاص بنا ، وأخيرًا ، حاول رسمه على الشاشة. تبدو مصفوفة المقياس كما يلي:
المعلمات sx و sy و sz على القطر الرئيسي تعني عدد المرات التي نريد زيادة الكائن فيها. إذا استبدلنا 10 ، 10 ، 10 في المصفوفة بدلاً من sx ، sy ، sz ، وضربنا هذه المصفوفة برؤوس المكعب ، فإن هذا سيجعل المكعب أكبر بعشر مرات ولن يكون 2 × 2 × 2 ، ولكن 20 × 20 في 20.بالنسبة لمصفوفة القياس ، وكذلك لمصفوفة الإزاحة ، نقوم بتنفيذ الطريقة في فئة Matrix ، والتي ستعيد المصفوفة مع الوسيطات التي تم استبدالها بالفعل:static getScale(sx, sy, sz) {
return [
[sx, 0, 0, 0],
[0, sy, 0, 0],
[0, 0, sz, 0],
[0, 0, 0, 1],
]
}
ناقل التصور
إذا حاولنا الآن رسم مكعب بخطوط باستخدام الإحداثيات الحالية للقمم ، فسوف نحصل على مكعب صغير جدًا ثنائي البكسل في الزاوية اليسرى العلوية من الشاشة ، لأن أصل اللوحة موجود. دعنا ننتقل عبر جميع رؤوس المكعب ونضربها في مصفوفة التحجيم لجعل المكعب أكبر ، ثم بمصفوفة الإزاحة لرؤية المكعب ليس في الزاوية اليسرى العليا ، ولكن في منتصف الشاشة ، لدي كود لتعداد الذروات مع ضرب المصفوفة أدناه مجموعة من الحواف ، وتبدو كما يلي:const sceneVertices = []
for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
Matrix.getScale(100, 100, 100),
vertices[i]
);
vertex = Matrix.multiplyVector(
Matrix.getTranslation(400, -300, 0),
vertex
);
sceneVertices.push(vertex);
}
يرجى ملاحظة أننا لا نغير الرؤوس الأولية للمكعب ، ولكننا نحفظ نتيجة الضرب في المشهد Vertices المصفوفة ، لأننا قد نرسم عدة مكعبات بأحجام مختلفة بإحداثيات مختلفة ، وإذا قمنا بتغيير الإحداثيات الأولية ، فلن نتمكن من رسم المكعب التالي ، ر .إلى. لا يوجد شيء نبدأ منه ، فإن الإحداثيات الأولية ستفسد بالمكعب الأول. في الكود أعلاه ، قمت بزيادة المكعب الأصلي بمقدار 100 مرة في جميع الاتجاهات ، عن طريق ضرب جميع القمم في مصفوفة التحجيم بالحجج 100 ، 100 ، 100 ، وقمت أيضًا بنقل جميع رؤوس المكعب إلى اليمين وأقل بمقدار 400 و -300 بكسل ، على التوالي ، لأن لدينا أحجام اللوحات من المادة السابقة هي 800 × 600 ، وستكون فقط نصف عرض وارتفاع منطقة الرسم ، وبعبارة أخرى ، المركز.لقد انتهينا من القمم حتى الآن ، لكننا ما زلنا بحاجة إلى رسم كل هذا باستخدام drawLine ومجموعة الحواف ، دعنا نكتب حلقة أخرى أسفل حلقة القمم لتكرارها على الحواف ونرسم جميع الخطوط فيها:drawer.clearSurface()
for (let i = 0, l = edges.length ; i < l ; i++) {
const e = edges[i]
drawer.drawLine(
sceneVertices[e[0]].x,
sceneVertices[e[0]].y,
sceneVertices[e[1]].x,
sceneVertices[e[1]].y,
0, 0, 255
)
}
ctx.putImageData(imageData, 0, 0)
تذكر أنه في المقالة الأخيرة بدأنا في الرسم بالكامل عن طريق مسح الشاشة من الحالة السابقة عن طريق استدعاء طريقة clearSurface ، ثم أقوم بالتكرار على جميع وجوه المكعب وأرسم المكعب بخطوط زرقاء (0 ، 0 ، 255) ، وأخذ إحداثيات الخطوط من المشهد مصفوفة Vertices ، t .إلى. هناك بالفعل رؤوس متدرجة ومتحركة في الدورة السابقة ، لكن مؤشرات هذه القمم تتزامن مع مؤشرات القمم الأصلية من مصفوفة القمم ، لأن قمت بمعالجتها ووضعها في مجموعة المشهد sceneVertices دون تغيير الترتيب. إذا قمنا بتشغيل الكود الآن ، فلن نرى أي شيء على الشاشة. هذا لأنه في نظام الإحداثيات الخاص بنا ، ينظر Y للأعلى ، وفي نظام الإحداثيات ، تبدو اللوحة القماشية لأسفل. اتضح أن هناك مكعبنا ، ولكنه خارج الشاشة ولإصلاح ذلك ، نحتاج إلى قلب الصورة في Y (مرآة) قبل رسم بكسل في فئة درج. حتى الآن ، سيكون هذا الخيار كافيًا بالنسبة لنا ، ونتيجة لذلك ، يبدو رمز رسم بكسل بالنسبة لي كما يلي:drawPixel(x, y, r, g, b) {
const offset = (this.width * -y + x) * 4;
if (x >= 0 && x < this.width && -y >= 0 && y < this.height) {
this.surface[offset] = r;
this.surface[offset + 1] = g;
this.surface[offset + 2] = b;
this.surface[offset + 3] = 255;
}
}
يمكن ملاحظة أنه في صيغة الحصول على الإزاحة ، يكون Y الآن بعلامة ناقص ويظهر المحور الآن في الاتجاه الذي نحتاج إليه ، وفي هذه الطريقة أيضًا أضفت فحصًا لتجاوز حدود صفيف البكسل. ظهرت بعض التحسينات الأخرى في فئة Drawer بسبب التعليقات على المقالة السابقة ، لذلك أنشر فئة Drawer بأكملها مع بعض التحسينات ويمكنك استبدال الدرج القديم بهذا:رمز فئة درج محسنclass Drawer {
surface = null;
width = 0;
height = 0;
constructor(surface, width, height) {
this.surface = surface;
this.width = width;
this.height = height;
}
drawPixel(x, y, r, g, b) {
const offset = (this.width * -y + x) * 4;
if (x >= 0 && x < this.width && -y >= 0 && y < this.height) {
this.surface[offset] = r;
this.surface[offset + 1] = g;
this.surface[offset + 2] = b;
this.surface[offset + 3] = 255;
}
}
drawLine(x1, y1, x2, y2, r = 0, g = 0, b = 0) {
const round = Math.trunc;
x1 = round(x1);
y1 = round(y1);
x2 = round(x2);
y2 = round(y2);
const c1 = y2 - y1;
const c2 = x2 - x1;
const length = Math.max(
Math.abs(c1),
Math.abs(c2)
);
const xStep = c2 / length;
const yStep = c1 / length;
for (let i = 0 ; i <= length ; i++) {
this.drawPixel(
Math.trunc(x1 + xStep * i),
Math.trunc(y1 + yStep * i),
r, g, b,
);
}
}
clearSurface() {
const surfaceSize = this.width * this.height * 4;
for (let i = 0; i < surfaceSize; i++) {
this.surface[i] = 0;
}
}
}
const drawer = new Drawer(
imageData.data,
imageData.width,
imageData.height
);
إذا قمت بتشغيل الكود الآن ، فستظهر الصورة التالية على الشاشة:هنا يمكنك أن ترى أن هناك مربع في المركز ، على الرغم من أننا توقعنا الحصول على مكعب ، ما الأمر؟ في الواقع - هذا هو المكعب ، إنه يقف تمامًا محاذاة تمامًا تمامًا مع أحد الوجوه (الجانب) تجاهنا ، لذلك لا نرى ما تبقى منه. أيضًا ، لم نتعرف بعد على الإسقاطات ، وبالتالي لا يصبح الوجه الخلفي للمكعب أصغر مع المسافة ، كما هو الحال في الحياة الحقيقية. من أجل التأكد من أن هذا هو مكعب بالفعل ، دعنا نديره قليلاً حتى يبدو وكأنه الصورة التي رأيناها سابقًا عندما قمنا بتشكيل مصفوفة الذروة. من أجل تدوير الصورة ثلاثية الأبعاد ، يمكنك استخدام 3 مصفوفات خاصة ، لأن يمكننا التدوير حول أحد المحاور X أو Y أو Z ، مما يعني أنه لكل محور سيكون هناك مصفوفة دوران خاصة به (هناك طرق أخرى للتدوير ، ولكن هذا هو موضوع المقالات التالية). إليك ما تبدو عليه هذه المصفوفات:إذا قمنا بضرب رؤوس المكعب بإحدى هذه المصفوفات ، فسيتم تدوير المكعب بالزاوية المحددة (أ) حول المحور ، مصفوفة الدوران التي سنختار حولها. هناك بعض الميزات عند تدوير عدة محاور في وقت واحد ، وسنلقي نظرة عليها أدناه. كما ترى من مثال المصفوفة ، يستخدمون دالتين sin و cos ، ولدى JavaScript بالفعل وظيفة لحساب Math.sin (a) و Math.cos (a) ، لكنهما يعملان بقياس راديان للزوايا ، والتي قد لا تبدو الأكثر ملاءمة إذا أردنا تدوير النموذج. على سبيل المثال ، من الأنسب بالنسبة لي تحويل شيء 90 درجة (مقياس درجة) ، وهو ما يعنيه مقياس راديانPi / 2(هناك أيضًا قيمة Pi تقريبية في JS ، وهذا هو Math.PI الثابت). دعنا نضيف 3 طرق إلى فئة Matrix للحصول على مصفوفات الدوران ، بزاوية دوران مقبولة بالدرجات ، والتي سنحولها إلى وحدات راديان ، لأن إنها ضرورية لكي تعمل دالات sin / cos:static getRotationX(angle) {
const rad = Math.PI / 180 * angle;
return [
[1, 0, 0, 0],
[0, Math.cos(rad), -Math.sin(rad), 0],
[0, Math.sin(rad), Math.cos(rad), 0],
[0, 0, 0, 1],
];
}
static getRotationY(angle) {
const rad = Math.PI / 180 * angle;
return [
[Math.cos(rad), 0, Math.sin(rad), 0],
[0, 1, 0, 0],
[-Math.sin(rad), 0, Math.cos(rad), 0],
[0, 0, 0, 1],
];
}
static getRotationZ(angle) {
const rad = Math.PI / 180 * angle;
return [
[Math.cos(rad), -Math.sin(rad), 0, 0],
[Math.sin(rad), Math.cos(rad), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
];
}
تبدأ جميع الطرق الثلاث بتحويل الدرجات إلى راديان ، وبعد ذلك نستبدل زاوية الدوران بالراديان في مصفوفة الدوران ، لتمرير الزوايا إلى دالتي sin و cos. لماذا تكون المصفوفة بهذه الصفة ، يمكنك قراءة المزيد على المحور في المقالات المواضيعية ، مع شرح مفصل للغاية ، وإلا يمكنك أن تدرك هذه المصفوفات كصيغ تم حسابها لنا ويمكننا التأكد من أنها تعمل.أعلاه في الكود ، نفذنا دورتين ، الأولى تحول القمم ، والثانية ترسم خطوطًا بمؤشرات القمة ، ونتيجة لذلك ، نحصل على صورة من القمم على الشاشة ، ودعنا نسمي هذا القسم من الكود خط أنابيب التصور. الناقل لأننا نأخذ الذروة ونقوم بدورنا بعمليات مختلفة معها ، الحجم ، التحول ، الدوران ، التقديم ، كما هو الحال في الناقل الصناعي العادي. الآن دعنا نضيف إلى الدورة الأولى في خط أنابيب التصور ، بالإضافة إلى القياس ، الدوران حول المحاور. أولاً ، سوف أقوم باستدارة X ، ثم حول Y ، ثم زيادة النموذج ونقله (آخر إجراءين موجودان بالفعل) ، لذلك سيكون رمز الحلقة بالكامل كما يلي:for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
Matrix.getRotationX(20),
vertices[i]
);
vertex = Matrix.multiplyVector(
Matrix.getRotationY(20),
vertex
);
vertex = Matrix.multiplyVector(
Matrix.getScale(100, 100, 100),
vertex
);
vertex = Matrix.multiplyVector(
Matrix.getTranslation(400, -300, 0),
vertex
);
sceneVertices.push(vertex);
}
في هذا المثال ، قمت بتدوير جميع القمم حول المحور X بمقدار 20 درجة ، ثم حول Y بمقدار 20 درجة وكان لدي بالفعل تحويلان متبقيان. إذا فعلت كل شيء بشكل صحيح ، فيجب أن يبدو المكعب ثلاثي الأبعاد الآن:الدوران حول المحاور له ميزة واحدة ، على سبيل المثال ، إذا قمت بتدوير المكعب أولاً حول المحور Y ، ثم حول المحور X ، فستختلف النتائج:هناك ميزات أخرى ، على سبيل المثال ، إذا قمت بتدوير المكعب 90 درجة على المحور X ، ثم 90 درجة على المحور Y ، وأخيرًا 90 درجة حول المحور Z ، فإن الدوران الأخير حول Z سيلغي الدوران حول X ، وتحصل على نفس تكون النتيجة كما لو كنت قد قمت للتو بتدوير الشكل 90 درجة حول المحور Y. لمعرفة سبب حدوث ذلك ، خذ أي كائن مستطيل (أو مكعب) في يديك (على سبيل المثال ، مكعب روبيك المجمع) ، وتذكر الوضع الأولي للجسم وقم بتدويره 90 درجة أولاً حول X التخيلي ، ثم 90 درجة حول Y و 90 درجة حول Z وتذكر أي جانب أصبح لك ، ثم ابدأ من الموضع الأولي الذي تذكرته سابقًا وافعل الشيء نفسه ، بإزالة المنعطفين من X و Z ، الدوران فقط ص - سترى أن النتيجة هي نفسها.الآن لن نقوم بحل هذه المشكلة وندخل تفاصيلها ، مثل هذا التناوب في الوقت الحالي يناسبنا تمامًا ، لكننا سنذكر هذه المشكلة في الجزء الثالث (إذا كنت ترغب في فهم المزيد الآن ، فحاول البحث عن مقالات على المحور بواسطة الاستعلام "قفل مفصلي") .لنقم الآن بتحسين الكود الخاص بنا قليلاً ، فقد ذكر أعلاه أنه يمكن دمج تحويلات المصفوفة مع بعضها البعض عن طريق ضرب مصفوفات التحويل. دعونا نحاول عدم ضرب كل متجه أولاً في مصفوفة الدوران حول X ، ثم حول Y ، ثم القياس وفي نهاية الحركة ، أولاً ، قبل الحلقة ، نضرب جميع المصفوفات ، وفي الحلقة سنقوم بضرب كل قمة في مصفوفة واحدة فقط ، ولدي الكود خرج مثل هذا:let matrix = Matrix.getRotationX(20);
matrix = Matrix.multiply(
Matrix.getRotationY(20),
matrix
);
matrix = Matrix.multiply(
Matrix.getScale(100, 100, 100),
matrix,
);
matrix = Matrix.multiply(
Matrix.getTranslation(400, -300, 0),
matrix,
);
const sceneVertices = [];
for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
matrix,
vertices[i]
);
sceneVertices.push(vertex);
}
في هذا المثال ، يتم تنفيذ مجموعة التحولات مرة واحدة قبل الدورة ، وبالتالي لدينا مضاعفة مصفوفة واحدة فقط مع كل قمة. إذا قمت بتشغيل هذا الرمز ، يجب أن يبقى نمط المكعب كما هو.دعنا نضيف أبسط الرسوم المتحركة ، أي أننا سنغير زاوية الدوران حول المحور Y في الفاصل الزمني ، على سبيل المثال ، سنقوم بتغيير زاوية الدوران حول المحور Y بمقدار درجة واحدة ، كل 100 مللي ثانية. للقيام بذلك ، ضع رمز خط التصور في دالة setInterval ، التي استخدمناها أولاً في المقالة الأولى. يبدو رمز مسار الرسوم المتحركة كما يلي:let angle = 0
setInterval(() => {
let matrix = Matrix.getRotationX(20)
matrix = Matrix.multiply(
Matrix.getRotationY(angle += 1),
matrix
)
matrix = Matrix.multiply(
Matrix.getScale(100, 100, 100),
matrix,
)
matrix = Matrix.multiply(
Matrix.getTranslation(400, -300, 0),
matrix,
)
const sceneVertices = []
for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
matrix,
vertices[i]
)
sceneVertices.push(vertex)
}
drawer.clearSurface()
for (let i = 0, l = edges.length ; i < l ; i++) {
const e = edges[i]
drawer.drawLine(
sceneVertices[e[0]].x,
sceneVertices[e[0]].y,
sceneVertices[e[1]].x,
sceneVertices[e[1]].y,
0, 0, 255
)
}
ctx.putImageData(imageData, 0, 0)
}, 100)
يجب أن تكون النتيجة كما يلي:آخر شيء سنفعله في هذا الجزء هو عرض محاور نظام الإحداثيات على الشاشة بحيث تكون مرئية حولها حيث يدور مكعبنا. نرسم المحور Y من المركز إلى الأعلى ، بطول 200 بكسل ، والمحور X إلى اليمين ، بطول 200 بكسل أيضًا ، والمحور Z ، ونرسم 150 بكسل لأسفل ولليسار (قطريًا) ، كما هو موضح في بداية المقالة في شكل نظام الإحداثيات الأيمن . لنبدأ بالجزء الأبسط ، هذه هي المحاور X ، Y ، لأن يتغير خطهم في اتجاه واحد فقط. بعد الحلقة التي ترسم المكعب (حلقة الحواف) أضف عرض المحور X ، Y:const center = new Vector(400, -300, 0)
drawer.drawLine(
center.x, center.y,
center.x, center.y + 200,
150, 150, 150
)
drawer.drawLine(
center.x, center.y,
center.x + 200, center.y,
150, 150, 150
)
المتجه المركزي هو منتصف نافذة الرسم ، لأنه أشرنا إلى أن الأبعاد الحالية هي 800 × 600 ، و -300 بالنسبة لـ Y ، لأن تقلب وظيفة drawPixel Y وتجعل اتجاهها مناسبًا للقماش (في اللوحة ، تبدو Y لأسفل). ثم نرسم محورين باستخدام drawLine ، ونحرك أولاً Y 200 بكسل لأعلى (نهاية خط المحور Y) ، ثم X 200 بكسل إلى اليمين (نهاية خط المحور X). نتيجة:الآن دعونا نرسم خط المحور Z ، فهو قطري لأسفل \ اليسار ومتجه الإزاحة سيكون [-1 ، -1 ، 0] ونحتاج أيضًا إلى رسم خط بطول 150 بكسل ، أي يجب أن يكون متجه الإزاحة [-1 ، -1 ، 0] 150 طولًا ، والخيار الأول هو [-150 ، -150 ، 0] ، ولكن إذا حسبنا طول هذا المتجه ، فسيكون حوالي 212 بكسل. ناقشنا سابقًا في هذه المقالة كيفية الحصول على متجه للطول المطلوب بشكل صحيح. بادئ ذي بدء ، نحن بحاجة إلى تطبيعه من أجل أن يؤدي إلى طول 1 ، ثم ضرب العدد الذي نريد أن نحصل عليه ، في حالتنا هو 150. وأخيرًا ، نجمع إحداثيات مركز الشاشة ومتجه الإزاحة للمحور Z ، لذلك نصل إلى حيث يجب أن ينتهي خط المحور Z. دعنا نكتب الكود ، بعد الكود الناتج من محورين سابقين لرسم خط المحور Z:const zVector = new Vector(-1, -1, 0);
const zCoords = Vector.add(
center,
zVector.normalize().multiplyByScalar(150)
);
drawer.drawLine(
center.x, center.y,
zCoords.x, zCoords.y,
150, 150, 150
);
ونتيجة لذلك ، تحصل على جميع المحاور الثلاثة للطول المطلوب:في هذا المثال ، يُظهر المحور Z فقط نظام الإحداثيات الذي لدينا ، قمنا برسمه قطريًا بحيث يمكن رؤيته ، لأن المحور Z الحقيقي عمودي على نظرتنا ، ويمكننا رسمه بنقطة على الشاشة ، والتي لن تكون جميلة.في المجموع ، في هذه المقالة ، فهمنا بشكل أساسي أنظمة الإحداثيات والمتجهات ومع بعض العمليات عليها والمصفوفات وأدوارها في تحويلات الإحداثيات وفرز القمم وكتب ناقلًا بسيطًا لتصور مكعب ومحاور نظام الإحداثيات ، وتثبيت النظرية بالممارسة. كل كود التطبيق متاح تحت المفسد:رمز التطبيق بالكاملconst ctx = document.getElementById('surface').getContext('2d');
const imageData = ctx.createImageData(800, 600);
class Vector {
x = 0;
y = 0;
z = 0;
w = 1;
constructor(x, y, z, w = 1) {
this.x = x;
this.y = y;
this.z = z;
this.w = w;
}
multiplyByScalar(s) {
this.x *= s;
this.y *= s;
this.z *= s;
return this;
}
static add(v1, v2) {
return new Vector(
v1.x + v2.x,
v1.y + v2.y,
v1.z + v2.z,
);
}
getLength() {
return Math.sqrt(
this.x * this.x + this.y * this.y + this.z * this.z
);
}
normalize() {
const length = this.getLength();
this.x /= length;
this.y /= length;
this.z /= length;
return this;
}
}
class Matrix {
static multiply(a, b) {
const m = [
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
];
for (let i = 0 ; i < 4 ; i++) {
for(let j = 0 ; j < 4 ; j++) {
m[i][j] = a[i][0] * b[0][j] +
a[i][1] * b[1][j] +
a[i][2] * b[2][j] +
a[i][3] * b[3][j];
}
}
return m;
}
static getRotationX(angle) {
const rad = Math.PI / 180 * angle;
return [
[1, 0, 0, 0],
[0, Math.cos(rad), -Math.sin(rad), 0],
[0, Math.sin(rad), Math.cos(rad), 0],
[0, 0, 0, 1],
];
}
static getRotationY(angle) {
const rad = Math.PI / 180 * angle;
return [
[Math.cos(rad), 0, Math.sin(rad), 0],
[0, 1, 0, 0],
[-Math.sin(rad), 0, Math.cos(rad), 0],
[0, 0, 0, 1],
];
}
static getRotationZ(angle) {
const rad = Math.PI / 180 * angle;
return [
[Math.cos(rad), -Math.sin(rad), 0, 0],
[Math.sin(rad), Math.cos(rad), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
];
}
static getTranslation(dx, dy, dz) {
return [
[1, 0, 0, dx],
[0, 1, 0, dy],
[0, 0, 1, dz],
[0, 0, 0, 1],
];
}
static getScale(sx, sy, sz) {
return [
[sx, 0, 0, 0],
[0, sy, 0, 0],
[0, 0, sz, 0],
[0, 0, 0, 1],
];
}
static multiplyVector(m, v) {
return new Vector(
m[0][0] * v.x + m[0][1] * v.y + m[0][2] * v.z + m[0][3] * v.w,
m[1][0] * v.x + m[1][1] * v.y + m[1][2] * v.z + m[1][3] * v.w,
m[2][0] * v.x + m[2][1] * v.y + m[2][2] * v.z + m[2][3] * v.w,
m[3][0] * v.x + m[3][1] * v.y + m[3][2] * v.z + m[3][3] * v.w,
);
}
}
class Drawer {
surface = null;
width = 0;
height = 0;
constructor(surface, width, height) {
this.surface = surface;
this.width = width;
this.height = height;
}
drawPixel(x, y, r, g, b) {
const offset = (this.width * -y + x) * 4;
if (x >= 0 && x < this.width && -y >= 0 && -y < this.height) {
this.surface[offset] = r;
this.surface[offset + 1] = g;
this.surface[offset + 2] = b;
this.surface[offset + 3] = 255;
}
}
drawLine(x1, y1, x2, y2, r = 0, g = 0, b = 0) {
const round = Math.trunc;
x1 = round(x1);
y1 = round(y1);
x2 = round(x2);
y2 = round(y2);
const c1 = y2 - y1;
const c2 = x2 - x1;
const length = Math.max(
Math.abs(c1),
Math.abs(c2)
);
const xStep = c2 / length;
const yStep = c1 / length;
for (let i = 0 ; i <= length ; i++) {
this.drawPixel(
Math.trunc(x1 + xStep * i),
Math.trunc(y1 + yStep * i),
r, g, b,
);
}
}
clearSurface() {
const surfaceSize = this.width * this.height * 4;
for (let i = 0; i < surfaceSize; i++) {
this.surface[i] = 0;
}
}
}
const drawer = new Drawer(
imageData.data,
imageData.width,
imageData.height
);
const vertices = [
new Vector(-1, 1, 1),
new Vector(-1, 1, -1),
new Vector(1, 1, -1),
new Vector(1, 1, 1),
new Vector(-1, -1, 1),
new Vector(-1, -1, -1),
new Vector(1, -1, -1),
new Vector(1, -1, 1),
];
const edges = [
[0, 1],
[1, 2],
[2, 3],
[3, 0],
[0, 4],
[1, 5],
[2, 6],
[3, 7],
[4, 5],
[5, 6],
[6, 7],
[7, 4],
];
let angle = 0;
setInterval(() => {
let matrix = Matrix.getRotationX(20);
matrix = Matrix.multiply(
Matrix.getRotationY(angle += 1),
matrix
);
matrix = Matrix.multiply(
Matrix.getScale(100, 100, 100),
matrix,
);
matrix = Matrix.multiply(
Matrix.getTranslation(400, -300, 0),
matrix,
);
const sceneVertices = [];
for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
matrix,
vertices[i]
);
sceneVertices.push(vertex);
}
drawer.clearSurface();
for (let i = 0, l = edges.length ; i < l ; i++) {
const e = edges[i];
drawer.drawLine(
sceneVertices[e[0]].x,
sceneVertices[e[0]].y,
sceneVertices[e[1]].x,
sceneVertices[e[1]].y,
0, 0, 255
);
}
const center = new Vector(400, -300, 0)
drawer.drawLine(
center.x, center.y,
center.x, center.y + 200,
150, 150, 150
);
drawer.drawLine(
center.x, center.y,
center.x + 200, center.y,
150, 150, 150
);
const zVector = new Vector(-1, -1, 0, 0);
const zCoords = Vector.add(
center,
zVector.normalize().multiplyByScalar(150)
);
drawer.drawLine(
center.x, center.y,
zCoords.x, zCoords.y,
150, 150, 150
);
ctx.putImageData(imageData, 0, 0);
}, 100);
ماذا بعد؟
في الجزء التالي ، سننظر في كيفية التحكم في الكاميرا وكيفية عمل الإسقاط (كلما كان الكائن أصغر ، كلما كان أصغر) ، والتعرف على المثلثات ومعرفة كيفية بناء نماذج ثلاثية الأبعاد منها ، وتحليل ما هي المعايير الطبيعية ولماذا هناك حاجة إليها.