تحسبًا لبدء الدورة التدريبية "خوارزميات للمطورين" أعدت لك ترجمة لمواد أخرى مفيدة.
ترميز هوفمان هو خوارزمية ضغط البيانات التي تصيغ الفكرة الأساسية لضغط الملف. في هذه المقالة ، سوف نتحدث عن الترميز الثابت والمتغير الطول ، والرموز التي تم فك تشفيرها بشكل فريد ، وقواعد البادئة ، وبناء شجرة هوفمان.نحن نعلم أن كل حرف يتم تخزينه كتسلسل من 0 و 1 ويستغرق 8 بتات. وهذا ما يسمى ترميز بطول ثابت لأن كل حرف يستخدم نفس عدد البتات الثابت للتخزين.لنفترض أن النص معطى. كيف يمكننا تقليل مقدار المساحة المطلوبة لتخزين حرف واحد؟الفكرة الأساسية هي الترميز بطول متغير. يمكننا استخدام حقيقة أن بعض الأحرف في النص أكثر شيوعًا من غيرها ( انظر هنا ) لتطوير خوارزمية تمثل نفس تسلسل الأحرف بتات أقل. عند ترميز طول متغير ، نقوم بتعيين عدد متغير من البتات للأحرف اعتمادًا على تكرار ظهورها في هذا النص. في النهاية ، قد تستغرق بعض الشخصيات 1 بت فقط ، والبعض الآخر 2 بت ، 3 أو أكثر. إن مشكلة تشفير الطول المتغير ليست سوى فك الشفرة اللاحق للتسلسل.كيف ، مع معرفة تسلسل البتات ، لفك تشفيرها بشكل فريد؟خذ بعين الاعتبار سلسلة "aabacdab" . يحتوي على 8 أحرف ، وعند ترميز طول ثابت ، ستكون هناك حاجة إلى 64 بت لتخزينه. لاحظ أن تردد الحروف "a" و "b" و "c" و "d" هو 4 و 2 و 1 و 1 على التوالي. دعونا نحاول أن نتخيل "aabacdab" بتات أقل ، باستخدام حقيقة أن "a" أكثر شيوعًا من "b" و "b" أكثر شيوعًا من "c" و "d" . بادئ ذي بدء ، نقوم بتشفير "a" باستخدام بت واحد يساوي 0 ، "b" ، نعين رمزًا من بتين 11 ، وباستخدام ثلاثة بتات 100 و 011 ، نقوم بتشفير "c" و"D" .ونتيجة لذلك ، سننجح:وبالتالي ، نقوم بترميز السلسلة "aabacdab" بالشكل 00110100011011 (0 | 0 | 11 | 0 | 100 | 011 | 0 | 11) باستخدام الرموز الموضحة أعلاه. ومع ذلك ، فإن المشكلة الرئيسية ستكون فك التشفير. عندما نحاول فك ترميز الخط 00110100011011 ، نحصل على نتيجة غامضة ، حيث يمكن تمثيلها على النحو التالي:0|011|0|100|011|0|11 adacdab
0|0|11|0|100|0|11|011 aabacabd
0|011|0|100|0|11|0|11 adacabab
...إلخ.لتجنب هذا الغموض ، يجب أن نتأكد من أن تشفيرنا يفي بمفهوم مثل قاعدة البادئة ، مما يعني بدوره أنه يمكن فك الشفرات بطريقة فريدة واحدة فقط. تضمن قاعدة البادئة عدم وجود رمز لبادئة أخرى. نقصد بالشفرة البتات المستخدمة لتمثيل شخصية معينة. في المثال أعلاه ، 0 هي البادئة 011 ، التي تنتهك قاعدة البادئة. لذا ، إذا كانت رموزنا تفي بقاعدة البادئة ، فيمكننا فك تشفيرها بشكل فريد (والعكس صحيح).دعنا نراجع المثال أعلاه. هذه المرة سوف نخصص الأحرف "a" و "b" و "c" و "d" الرموز التي تلبي قاعدة البادئة.باستخدام هذا الترميز ، سيتم ترميز السلسلة "aabacdab" بالشكل 00100100011010 (0 | 0 | 10 | 0 | 100 | 011 | 0 | 10) . وهنا 00100100011010 يمكننا فك شفرة والعودة إلى خطنا الأصلي "aabacdab" .ترميز هوفمان
الآن بعد أن اكتشفنا الترميز بطول متغير وقاعدة بادئة ، دعنا نتحدث عن ترميز هوفمان.تعتمد الطريقة على إنشاء أشجار ثنائية. في ذلك ، يمكن أن تكون العقدة محدودة أو داخلية. في البداية ، تعتبر جميع العقد أوراقًا (أوراق) ، والتي تمثل الرمز نفسه ووزنه (أي تكرار الحدوث). تحتوي العقد الداخلية على وزن الشخصية وتشير إلى عقدتين منحدر. بالاتفاق العام ، يمثل البت "0" متابعة على الفرع الأيسر ، ويمثل "1" على اليمين. في شجرة كاملة هناك N الأوراق و N-1 العقد الداخلية. من المستحسن عند بناء شجرة هوفمان ، التخلص من الأحرف غير المستخدمة للحصول على رموز الطول الأمثل.سنستخدم قائمة انتظار الأولوية لبناء شجرة هوفمان ، حيث ستُمنح العقدة ذات التردد الأقل أولوية قصوى. يتم وصف خطوات البناء أدناه:- قم بإنشاء عقدة طرفية لكل حرف وإضافتها إلى قائمة انتظار الأولوية.
- عندما تكون في الطابور لأكثر من ورقة واحدة ، قم بما يلي:
- إزالة العقدتين بأعلى أولوية (بأقل تردد) من قائمة الانتظار ؛
- قم بإنشاء عقدة داخلية جديدة حيث تكون هاتان العقدتان ورثة ، وسيكون تواتر الحدوث مساوياً لمجموع ترددات هاتين العقدتين.
- قم بإضافة عقدة جديدة إلى قائمة انتظار الأولوية.
- العقدة الوحيدة المتبقية ستكون الجذر ، وهذا سينهي بناء الشجرة.
تخيل أن لدينا نصًا يتكون فقط من الأحرف "a" و "b" و "c" و "d" و "e" وترددات ظهورها هي 15 و 7 و 6 و 6 و 5 على التوالي. فيما يلي الرسوم التوضيحية التي تعكس خطوات الخوارزمية.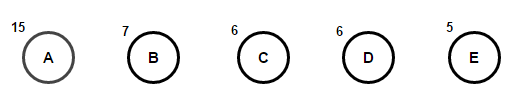
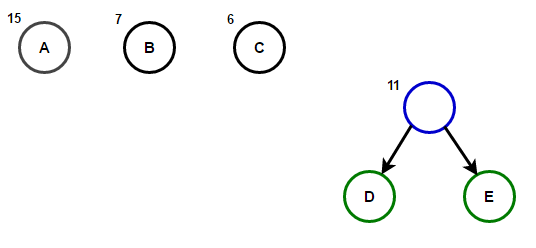
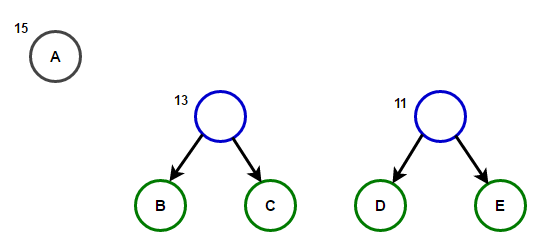
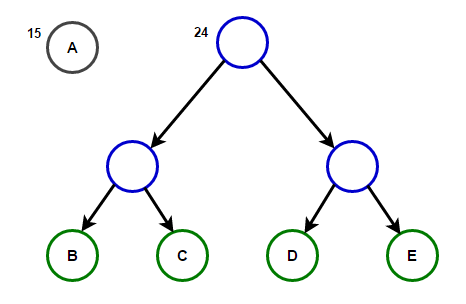
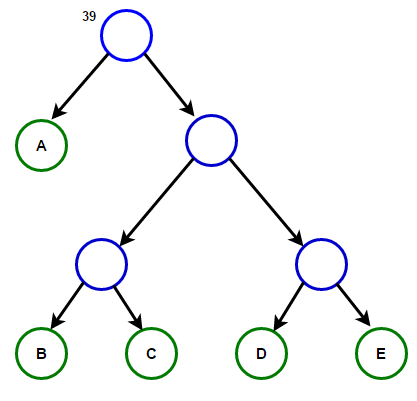 سيخزن المسار من الجذر إلى أي عقدة نهاية رمز البادئة الأمثل (المعروف أيضًا باسم رمز Huffman) المطابق للحرف المرتبط بهذه العقدة الطرفية.
سيخزن المسار من الجذر إلى أي عقدة نهاية رمز البادئة الأمثل (المعروف أيضًا باسم رمز Huffman) المطابق للحرف المرتبط بهذه العقدة الطرفية.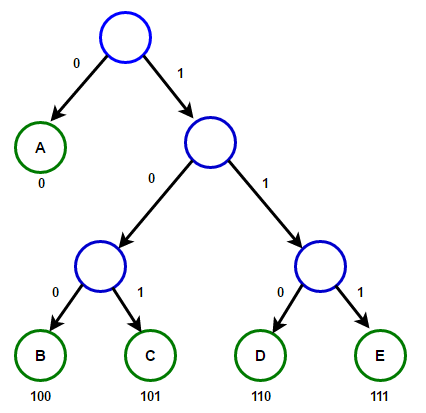 Huffman Treeأدناه ستجد تنفيذ خوارزمية ضغط Huffman في C ++ و Java:
Huffman Treeأدناه ستجد تنفيذ خوارزمية ضغط Huffman في C ++ و Java:#include <iostream>
#include <string>
#include <queue>
#include <unordered_map>
using namespace std;
struct Node
{
char ch;
int freq;
Node *left, *right;
};
Node* getNode(char ch, int freq, Node* left, Node* right)
{
Node* node = new Node();
node->ch = ch;
node->freq = freq;
node->left = left;
node->right = right;
return node;
}
struct comp
{
bool operator()(Node* l, Node* r)
{
return l->freq > r->freq;
}
};
void encode(Node* root, string str,
unordered_map<char, string> &huffmanCode)
{
if (root == nullptr)
return;
if (!root->left && !root->right) {
huffmanCode[root->ch] = str;
}
encode(root->left, str + "0", huffmanCode);
encode(root->right, str + "1", huffmanCode);
}
void decode(Node* root, int &index, string str)
{
if (root == nullptr) {
return;
}
if (!root->left && !root->right)
{
cout << root->ch;
return;
}
index++;
if (str[index] =='0')
decode(root->left, index, str);
else
decode(root->right, index, str);
}
void buildHuffmanTree(string text)
{
unordered_map<char, int> freq;
for (char ch: text) {
freq[ch]++;
}
priority_queue<Node*, vector<Node*>, comp> pq;
for (auto pair: freq) {
pq.push(getNode(pair.first, pair.second, nullptr, nullptr));
}
while (pq.size() != 1)
{
Node *left = pq.top(); pq.pop();
Node *right = pq.top(); pq.pop();
int sum = left->freq + right->freq;
pq.push(getNode('\0', sum, left, right));
}
Node* root = pq.top();
unordered_map<char, string> huffmanCode;
encode(root, "", huffmanCode);
cout << "Huffman Codes are :\n" << '\n';
for (auto pair: huffmanCode) {
cout << pair.first << " " << pair.second << '\n';
}
cout << "\nOriginal string was :\n" << text << '\n';
string str = "";
for (char ch: text) {
str += huffmanCode[ch];
}
cout << "\nEncoded string is :\n" << str << '\n';
int index = -1;
cout << "\nDecoded string is: \n";
while (index < (int)str.size() - 2) {
decode(root, index, str);
}
}
int main()
{
string text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
return 0;
}
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;
class Node
{
char ch;
int freq;
Node left = null, right = null;
Node(char ch, int freq)
{
this.ch = ch;
this.freq = freq;
}
public Node(char ch, int freq, Node left, Node right) {
this.ch = ch;
this.freq = freq;
this.left = left;
this.right = right;
}
};
class Huffman
{
public static void encode(Node root, String str,
Map<Character, String> huffmanCode)
{
if (root == null)
return;
if (root.left == null && root.right == null) {
huffmanCode.put(root.ch, str);
}
encode(root.left, str + "0", huffmanCode);
encode(root.right, str + "1", huffmanCode);
}
public static int decode(Node root, int index, StringBuilder sb)
{
if (root == null)
return index;
if (root.left == null && root.right == null)
{
System.out.print(root.ch);
return index;
}
index++;
if (sb.charAt(index) == '0')
index = decode(root.left, index, sb);
else
index = decode(root.right, index, sb);
return index;
}
public static void buildHuffmanTree(String text)
{
Map<Character, Integer> freq = new HashMap<>();
for (int i = 0 ; i < text.length(); i++) {
if (!freq.containsKey(text.charAt(i))) {
freq.put(text.charAt(i), 0);
}
freq.put(text.charAt(i), freq.get(text.charAt(i)) + 1);
}
PriorityQueue<Node> pq = new PriorityQueue<>(
(l, r) -> l.freq - r.freq);
for (Map.Entry<Character, Integer> entry : freq.entrySet()) {
pq.add(new Node(entry.getKey(), entry.getValue()));
}
while (pq.size() != 1)
{
Node left = pq.poll();
Node right = pq.poll();
int sum = left.freq + right.freq;
pq.add(new Node('\0', sum, left, right));
}
Node root = pq.peek();
Map<Character, String> huffmanCode = new HashMap<>();
encode(root, "", huffmanCode);
System.out.println("Huffman Codes are :\n");
for (Map.Entry<Character, String> entry : huffmanCode.entrySet()) {
System.out.println(entry.getKey() + " " + entry.getValue());
}
System.out.println("\nOriginal string was :\n" + text);
StringBuilder sb = new StringBuilder();
for (int i = 0 ; i < text.length(); i++) {
sb.append(huffmanCode.get(text.charAt(i)));
}
System.out.println("\nEncoded string is :\n" + sb);
int index = -1;
System.out.println("\nDecoded string is: \n");
while (index < sb.length() - 2) {
index = decode(root, index, sb);
}
}
public static void main(String[] args)
{
String text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
}
}
ملاحظة: الذاكرة المستخدمة في سلسلة الإدخال هي 47 * 8 = 376 بت ، والسلسلة المشفرة لا تأخذ سوى 194 بت ، أي يتم ضغط البيانات بحوالي 48٪. في برنامج C ++ أعلاه ، نستخدم فئة السلسلة لتخزين السلسلة المشفرة لجعل البرنامج قابل للقراءة.نظرًا لأن هياكل البيانات الفعالة لقائمة انتظار الأولوية تتطلب إدخال وقت O (تسجيل (N)) ، وفي شجرة ثنائية كاملة بأوراق N هناك عقد 2N-1 ، وشجرة Huffman هي شجرة ثنائية كاملة ، تعمل الخوارزمية لـ O (Nlog (N )) الوقت ، حيث N هو عدد الأحرف.مصادر:
en.wikipedia.org/wiki/Huffman_codingen.wikipedia.org/wiki/Variable-length_codewww.youtube.com/watch?v=5wRPin4oxCo
.