 هل يبدو هذا مألوفًا: "لقد بدأت في تطوير الويب بعد أخذ الدورات"؟ربما تريد تحسين معرفتك بأساسيات علوم الكمبيوتر من حيث هياكل البيانات والخوارزميات. سنتحدث اليوم عن بعض هياكل البيانات الأكثر شيوعًا باستخدام مثال JS.
هل يبدو هذا مألوفًا: "لقد بدأت في تطوير الويب بعد أخذ الدورات"؟ربما تريد تحسين معرفتك بأساسيات علوم الكمبيوتر من حيث هياكل البيانات والخوارزميات. سنتحدث اليوم عن بعض هياكل البيانات الأكثر شيوعًا باستخدام مثال JS.1. مكدس (مكالمات) (مكدس)
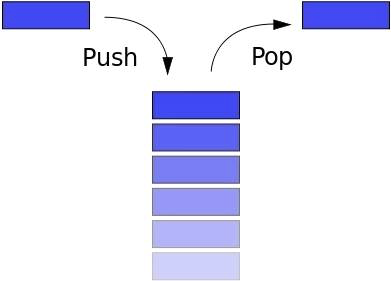 المكدس يتبع مبدأ LIFO (Last In First Out - Last In ، First Out). إذا قمت بتكديس الكتب فوق بعضها البعض وأردت أن تأخذ أقل كتاب ، فخذ أولاً الكتاب الأول ، ثم الكتاب التالي ، إلخ. يتيح لك الزر "رجوع" في المتصفح الانتقال (العودة) إلى الصفحة السابقة.يحتوي المكدس على الطرق التالية:
المكدس يتبع مبدأ LIFO (Last In First Out - Last In ، First Out). إذا قمت بتكديس الكتب فوق بعضها البعض وأردت أن تأخذ أقل كتاب ، فخذ أولاً الكتاب الأول ، ثم الكتاب التالي ، إلخ. يتيح لك الزر "رجوع" في المتصفح الانتقال (العودة) إلى الصفحة السابقة.يحتوي المكدس على الطرق التالية:- دفع: إضافة عنصر جديد
- pop: إزالة العنصر العلوي وإعادته
- نظرة خاطفة: عودة العنصر العلوي
- الطول: إرجاع عدد العناصر على المكدس
يحتوي المصفوفة في JS على سمات مكدس ، ولكننا سننشئها من البداية باستخدام الوظيفة Stack ():function Stack() {
this.count = 0
this.storage = {}
this.push = function(value) {
this.storage[this.count] = value
this.count++
}
this.pop = function() {
if (this.count === 0) return undefined
this.count--
let result = this.storage[this.count]
delete this.storage[this.count]
return result
}
this.peek = function() {
return this.storage[this.count - 1]
}
this.size = function() {
return this.count
}
}
2. قائمة الانتظار (قائمة الانتظار)
 يشبه قائمة الانتظار مكدس. الفرق هو أن قائمة الانتظار تتبع مبدأ FIFO (First In First Out - First in ، First out). عندما تقف في الطابور ، سيكون الأول فيه دائمًا.قائمة الانتظار بالطرق التالية:
يشبه قائمة الانتظار مكدس. الفرق هو أن قائمة الانتظار تتبع مبدأ FIFO (First In First Out - First in ، First out). عندما تقف في الطابور ، سيكون الأول فيه دائمًا.قائمة الانتظار بالطرق التالية:- enqueue: أدخل قائمة الانتظار ، أضف عنصرًا إلى النهاية
- dequeue: اترك قائمة الانتظار ، واحذف العنصر الأول وأعده
- الجبهة: احصل على العنصر الأول
- isEmpty: تحقق مما إذا كانت قائمة الانتظار فارغة
- الحجم: الحصول على عدد العناصر في قائمة الانتظار
يحتوي المصفوفة في JS على بعض سمات قائمة الانتظار ، لذا يمكننا استخدامها للتوضيح:function Queue() {
let collection = []
this.print = function() {
console.log(collection)
}
this.enqueue = function(element) {
collection.push(element)
}
this.dequeue = function() {
return collection.shift()
}
this.front = function() {
return collection[0]
}
this.isEmpty = function() {
return collection.length === 0
}
this.size = function() {
return collection.length
}
}
ترتيب الأولوية (الأولوية)
قائمة الانتظار لديها نسخة متقدمة. قم بتعيين أولوية لكل عنصر وسيتم فرز العناصر وفقًا لذلك:function PriorityQueue() {
...
this.enqueue = function(element) {
if (this.isEmpty()) {
collection.push(element)
} else {
let added = false
for (let i = 0; i < collection.length; i++) {
if (element[1] < collection[i][1]) {
collection.splice(i, 0, element)
added = true
break;
}
}
if (!added) {
collection.push(element)
}
}
}
}
اختبارات:let pQ = new PriorityQueue()
pQ.enqueue([gannicus, 3])
pQ.enqueue([spartacus, 1])
pQ.enqueue([crixus, 2])
pQ.enqueue([oenomaus, 4])
pQ.print()
نتيجة:[
[spartacus, 1],
[crixus, 2],
[gannicus, 3],
[oenomaus, 4]
]
3. قائمة مرتبطة (قائمة مرتبطة بالعُقد والروابط أو المؤشرات) (قائمة مرتبطة)
 حرفيا ، القائمة المرتبطة هي بنية بيانات متسلسلة حيث تتكون كل عقدة من جزأين: البيانات من العقدة والمؤشر إلى العقدة التالية. القائمة المرتبطة والصفيف الشرطي هي هياكل بيانات خطية مع تخزين متسلسل. الاختلافات هي كما يلي:تحتوي القائمة المرتبطة بشكل فردي على الطرق التالية:
حرفيا ، القائمة المرتبطة هي بنية بيانات متسلسلة حيث تتكون كل عقدة من جزأين: البيانات من العقدة والمؤشر إلى العقدة التالية. القائمة المرتبطة والصفيف الشرطي هي هياكل بيانات خطية مع تخزين متسلسل. الاختلافات هي كما يلي:تحتوي القائمة المرتبطة بشكل فردي على الطرق التالية:- الحجم: إرجاع عدد العقد
- الرأس: إرجاع العنصر الأول (الرأس - الرأس)
- إضافة: إضافة عنصر إلى النهاية (الذيل - الذيل)
- إزالة: إزالة عدة عقد
- indexOf: فهرس عقدة الإرجاع
- elementAt: إرجاع العقدة حسب الفهرس
- addAt: أدخل عقدة في مكان معين (حسب الفهرس)
- removeAt: إزالة عقدة معينة (حسب الفهرس)
function Node(element) {
this.element = element
this.next = null
}
function LinkedList() {
let length = 0
let head = null
this.size = function() {
return length
}
this.head = function() {
return head
}
this.add = function(element) {
let node = new Node(element)
if (head === null) {
head = node
} else {
let currentNode = head
while (currentNode.next) {
currentNode = currentNode.next
}
currentNode.next = node
}
length++
}
this.remove = function(element) {
let currentNode = head
let previousNode
if (currentNode.element !== element) {
head = currentNode.next
} else {
while (currentNode.element !== element) {
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
}
this.isEmpty = function() {
return length === 0
}
this.indexOf = function(element) {
let currentNode = head
let index = -1
while (currentNode) {
index++
if (currentNode.element === element) {
return index
}
currentNode = currentNode.next
}
return -1
}
this.elementAt = function(index) {
let currentNode = head
let count = 0
while (count < index) {
count++
currentNode = currentNode.next
}
return currentNode.element
}
this.addAt = function(index, element) {
let node = new Node(element)
let currentNode = head
let previousNode
let currentIndex = 0
if (index > length) return false
if (index === 0) {
node.next = currentNode
head = node
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
node.next = currentNode
previousNode.next = node
}
length++
}
this.removeAt = function(index) {
let currentNode = head
let previousNode
let currentIndex = 0
if (index < 0 || index >= length) return null
if (index === 0) {
head = currentIndex.next
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
return currentNode.element
}
}
4. جمع (القيم) (مجموعة)
 مجموعة (العديد) هي واحدة من المفاهيم الأساسية للرياضيات: مجموعة من الأشياء المحددة والمعزولة بشكل جيد. قدم ES6 مجموعة تحمل بعض التشابه مع صفيف. ومع ذلك ، لا تسمح المجموعة بتضمين عناصر مكررة ولا تحتوي على فهارس.تحتوي المجموعة القياسية على الطرق التالية:
مجموعة (العديد) هي واحدة من المفاهيم الأساسية للرياضيات: مجموعة من الأشياء المحددة والمعزولة بشكل جيد. قدم ES6 مجموعة تحمل بعض التشابه مع صفيف. ومع ذلك ، لا تسمح المجموعة بتضمين عناصر مكررة ولا تحتوي على فهارس.تحتوي المجموعة القياسية على الطرق التالية:- القيم: إرجاع جميع العناصر الموجودة في المجموعة
- الحجم: إرجاع عدد العناصر
- has: تحقق من وجود عنصر في المجموعة
- إضافة: إضافة عنصر
- إزالة: إزالة عنصر
- الاتحاد: إعادة منطقة تقاطع مجموعتين
- الفرق: إرجاع الاختلافات بين المجموعتين
- مجموعة فرعية: تحقق مما إذا كانت مجموعة واحدة مجموعة فرعية من مجموعة أخرى
function MySet() {
let collection = []
this.has = function(element) {
return (collection.indexOf(element) !== -1)
}
this.values = function() {
return collection
}
this.size = function() {
return collection.length
}
this.add = function(element) {
if (!this.has(element)) {
collection.push(element)
return true
}
return false
}
this.remove = function(element) {
if (this.has(element)) {
index = collection.indexOf(element)
collection.splice(index, 1)
return true
}
return false
}
this.union = function(otherSet) {
let unionSet = new MySet()
let firstSet = this.values()
let secondSet = otherSet.values()
firstSet.forEach(i => unionSet.add(i))
secondSet.forEach(i => unionSet.add(i))
}
this.intersection = function(otherSet) {
let intersectionSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (otherSet.has(e)) {
intersectionSet.add(e)
}
})
return intersectionSet
}
this.difference = function(otherSet) {
let differenceSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (!otherSet.has(e)) {
differenceSet.add(e)
}
})
return differenceSet
}
this.subset = function(otherSet) {
lat firstSet = this.values()
return firstSet.every(value => otherSet.has(value))
}
}
5. جدول التجزئة (جدول التجزئة)
 جدول التجزئة هو بنية بيانات مبنية على أساس القيمة الأساسية. نظرًا للسرعة العالية للبحث عن القيم حسب المفتاح ، يتم استخدامه في هياكل مثل الخريطة والقاموس والكائن. كما هو موضح في الشكل ، يحتوي جدول التجزئة على وظيفة التجزئة التي تحول المفاتيح إلى قائمة من الأرقام التي يتم استخدامها كأسماء (قيم) للمفاتيح. يمكن أن يصل وقت البحث عن القيمة الرئيسية إلى O (1). يجب أن تُرجع المفاتيح المتطابقة نفس القيمة - وهذا هو جوهر دالة التجزئة.يحتوي جدول التجزئة على الطرق التالية:
جدول التجزئة هو بنية بيانات مبنية على أساس القيمة الأساسية. نظرًا للسرعة العالية للبحث عن القيم حسب المفتاح ، يتم استخدامه في هياكل مثل الخريطة والقاموس والكائن. كما هو موضح في الشكل ، يحتوي جدول التجزئة على وظيفة التجزئة التي تحول المفاتيح إلى قائمة من الأرقام التي يتم استخدامها كأسماء (قيم) للمفاتيح. يمكن أن يصل وقت البحث عن القيمة الرئيسية إلى O (1). يجب أن تُرجع المفاتيح المتطابقة نفس القيمة - وهذا هو جوهر دالة التجزئة.يحتوي جدول التجزئة على الطرق التالية:- إضافة: إضافة زوج مفتاح / قيمة
- إزالة: إزالة زوج
- بحث: البحث عن القيمة حسب المفتاح
function hash(string, max) {
let hash = 0
for (let i = 0; i < string.length; i++) {
hash += string.charCodeAt(i)
}
return hash % max
}
function HashTable() {
let storage = []
const storageLimit = 4
this.add = function(key, value) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
storage[index] = [
[key, value]
]
} else {
let inserted = false
for (let i = 0; i < storage[index].len; i++) {
if (storage[index][i][0] === key) {
storage[index][i][1] = value
inserted = true
}
}
if (inserted === false) {
storage[index].push([key, value])
}
}
}
this.remove = function(key) {
let index = hash(key, storageLimit)
if (storage[index].length === 1 && storage[index][0][0] === key) {
delete storage[index]
} else {
for (let i = 0; i < storage[index]; i++) {
if (storage[index][i][0] === key) {
delete storage[index][i]
}
}
}
}
this.lookup = function(key) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
return undefined
} else {
for (let i = 0; i < storage[index].length; i++) {
if (storage[index][i][0] === key) {
return storage[index][i][1]
}
}
}
}
}
6. شجرة
 هيكل الشجرة هو هيكل متعدد الطبقات (متعدد المستويات). وهي أيضًا بنية غير خطية ، على عكس المصفوفة والمكدس وقائمة الانتظار. هذا الهيكل فعال للغاية من حيث إضافة العناصر والبحث عنها. فيما يلي بعض مفاهيم هيكل الشجرة:
هيكل الشجرة هو هيكل متعدد الطبقات (متعدد المستويات). وهي أيضًا بنية غير خطية ، على عكس المصفوفة والمكدس وقائمة الانتظار. هذا الهيكل فعال للغاية من حيث إضافة العناصر والبحث عنها. فيما يلي بعض مفاهيم هيكل الشجرة:- الجذر: عنصر الجذر ، ليس له أصل
- العقدة الأصلية: عقدة مباشرة للطبقة العليا (المستوى) ، يمكن أن تكون واحدة فقط
- العقدة الفرعية: عقدة مباشرة من المستوى الأدنى ، قد تكون هناك عدة
- الأشقاء: أبناء عقدة أم واحدة
- ورقة: عقدة بدون "أطفال"
- الحافة: فرع أو رابط (رابط) بين العقد
- المسار: المسار (مجموعة روابط) من عقدة البداية إلى العنصر الهدف
- ارتفاع الشجرة: عدد ارتباطات المسار الأطول من عنصر معين إلى عقدة ليس لها أطفال
- عمق العقدة: عدد الروابط من العقدة الجذرية إلى عنصر معين.
- درجة العقدة: عدد الأحفاد
فيما يلي مثال لشجرة بحث ثنائية (BST). لكل عقدة نسلان فقط ، العقدة اليسرى (التابعة) أصغر من العقدة (الأصل) الحالية ، والعقدة الأكبر أكبر: طرق هذه الشجرة هي كما يلي:
طرق هذه الشجرة هي كما يلي:- إضافة: إضافة عقدة
- findMin: احصل على العقدة الدنيا
- findMax: احصل على العقدة القصوى
- العثور على: العثور على عقدة معينة
- isPresent: تحقق من وجود عقدة معينة
- إزالة: إزالة العقدة
class Node {
constructor(data, left = null, right = null) {
this.data = data
this.left = left
this.right = right
}
}
class BST {
constructor() {
this.root = null
}
add(data) {
const node = this.root
if (node === null) {
this.root = new Node(data)
return
} else {
const searchTree = function(node) {
if (data < node.data) {
if (node.left === null) {
node.left = new Node(data)
return
} else if (node.left !== null) {
return searchTree(node.left)
}
} else if (data > node.data) {
if (node.right === null) {
node.right = new Node(data)
return
} else if (node.right !== null) {
return searchTree(node.right)
}
} else {
return null
}
}
return searchTree(node)
}
}
findMin() {
let current = this.root
while (current.left !== null) {
current = current.left
}
return current.data
}
findMax() {
let current = this.root
while (current.right !== null) {
current = current.right
}
return current.data
}
find(data) {
let current = this.root
while (current.data !== data) {
if (data < current.data) {
current = current.left
} else {
current = current.right
}
if (current === null) {
return null
}
}
return current
}
isPresent(data) {
let current = this.root
while (current) {
if (data === current.data) {
return true
}
data < current.data ? current = current.left : current = current.right
}
return false
}
remove(data) {
const removeNode = function(node, data) {
if (node === null) return null
if (data === node.data) {
if (node.left === null && node.right === null) return null
if (node.left === null) return node.right
if (node.right === null) return node.left
let tempNode = node.right
while (tempNode.left !== null) {
tempNode = tempNode.left
}
node.data = tempNode.data
node.right = removeNode(node.right, tempNode.data)
return node
} else if (data < node.data) {
node.left = removeNode(node.right, data)
return node
} else {
node.right = removeNode(node.right, data)
return node
}
}
this.root = removeNode(this.root, data)
}
}
اختبارات:const bst = new BST()
bst.add(4)
bst.add(2)
bst.add(6)
bst.add(1)
bst.add(3)
bst.add(5)
bst.add(7)
bst.remove(4)
console.log(bst.findMin())
console.log(bst.findMax())
bst.remove(7)
console.log(bst.findMax())
console.log(bst.isPresent(4))
نتيجة:1
7
6
false
7. شجرة محملة (بادئة) (Trie ، تقرأ كـ "try")
 شجرة البادئة هي نوع من شجرة البحث. يتم تخزين البيانات الموجودة فيه بالتسلسل (خطوة بخطوة) - تمثل كل عقدة شجرة خطوة واحدة. يتم استخدام شجرة البادئة في القواميس ، لأنها تسرع البحث بشكل كبير.كل عقدة شجرة هي حرف الأبجدية ، بعد فرع يؤدي إلى تشكيل كلمة. يحتوي أيضًا على "مؤشر منطقي" لتحديد أن العقدة الحالية هي الحرف الأخير.لدى شجرة البادئة الطرق التالية:
شجرة البادئة هي نوع من شجرة البحث. يتم تخزين البيانات الموجودة فيه بالتسلسل (خطوة بخطوة) - تمثل كل عقدة شجرة خطوة واحدة. يتم استخدام شجرة البادئة في القواميس ، لأنها تسرع البحث بشكل كبير.كل عقدة شجرة هي حرف الأبجدية ، بعد فرع يؤدي إلى تشكيل كلمة. يحتوي أيضًا على "مؤشر منطقي" لتحديد أن العقدة الحالية هي الحرف الأخير.لدى شجرة البادئة الطرق التالية:- إضافة: إضافة كلمة إلى القاموس
- isWord: تحقق من وجود كلمة
- طباعة: إرجاع جميع الكلمات
function Node() {
this.keys = new Map()
this.end = false
this.setEnd = function() {
this.end = true
}
this.isEnd = function() {
return this.end
}
}
function Trie() {
this.root = new Node()
this.add = function(input, node = this.root) {
if (input.length === 0) {
node.setEnd()
return
} else if (!node.keys.has(input[0])) {
node.keys.set(input[0], new Node())
return this.add(input.substr(1), node.key.get(input[0]))
} else {
return this.add(input.substr(1), node.keys.get(input[0]))
}
}
this.isWord = function(word) {
let node = this.root
while (word.length > 1) {
if (node.keys.has(word[0])) {
return false
} else {
node = node.keys.get(word[0])
word = word.substr(1)
}
}
return (node.keys.has(word) && node.keys.get(word).isEnd()) ? true : false
}
this.print = function() {
let words = new Array()
let search = function(node = this.root, string) {
if (node.keys.size !== 0) {
for (let letter of node.keys.keys()) {
search(node.keys.get(letter), string.concat(letter))
}
if (node.isEnd()) {
words.push(string)
}
} else {
string.length > 0 ? words.push(string) : undefined
return
}
}
search(this.root, new String())
return words.length > 0 ? words : null
}
}
8. الرسم البياني (الرسم البياني) (الرسم البياني)
 الرسم البياني ، المعروف أيضًا باسم الشبكة ، عبارة عن مجموعة من العقد المترابطة. هناك نوعان من الرسوم البيانية - موجه وغير موجه ، اعتمادًا على ما إذا كانت الروابط لها اتجاه. تُستخدم الرسوم البيانية في كل مكان ، على سبيل المثال ، لحساب أفضل مسار في تطبيقات الملاحة أو لإنشاء قائمة توصيات على الشبكات الاجتماعية.يمكن تقديم الرسوم البيانية في شكل قائمة أو مصفوفة.
الرسم البياني ، المعروف أيضًا باسم الشبكة ، عبارة عن مجموعة من العقد المترابطة. هناك نوعان من الرسوم البيانية - موجه وغير موجه ، اعتمادًا على ما إذا كانت الروابط لها اتجاه. تُستخدم الرسوم البيانية في كل مكان ، على سبيل المثال ، لحساب أفضل مسار في تطبيقات الملاحة أو لإنشاء قائمة توصيات على الشبكات الاجتماعية.يمكن تقديم الرسوم البيانية في شكل قائمة أو مصفوفة.قائمة
في هذه الحالة ، تقع جميع العقد الرئيسية على اليسار ، وأطفالهم على اليمين.
المصفوفة
في هذه الحالة ، يتم توزيع العقد في صفوف وأعمدة ، ويظهر تقاطع الصف والعمود العلاقة بين العقد: 0 يعني أن العقد غير متصلة ، 1 - العقد متصلة. يتم البحث في الرسم البياني بطريقتين - البحث الأول (البحث عن النفس أولاً ، BFS) والبحث العميق (البحث عن العمق ، DFS).خذ بعين الاعتبار BFS:
يتم البحث في الرسم البياني بطريقتين - البحث الأول (البحث عن النفس أولاً ، BFS) والبحث العميق (البحث عن العمق ، DFS).خذ بعين الاعتبار BFS:function bfs(graph, root) {
let nodesLen = {}
for (let i = 0; i < graph.length; i++) {
nodesLen[i] = Infinity
}
nodesLen[root] = 0
let queue = [root]
let current
while (queue.length !== 0) {
current = queue.shift()
let curConnected = graph[current]
let neighborIdx = []
let idx = curConnected.indexOf(1)
while (idx !== -1) {
neighborIdx.push(idx)
idx = curConnected.indexOf(1, idx + 1)
}
for (let i = 0; i < neighborIdx.length; i++) {
if (nodesLen[neighborIdx[i]] === Infinity) {
nodesLen[neighborIdx[i]] = nodesLen[current] + 1
queue.push(neighborIdx[i])
}
}
}
return nodesLen
}
اختبارات:let graph = [
[0, 1, 1, 1, 0],
[0, 0, 1, 0, 0],
[1, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 1, 0, 0, 0]
]
console.log(bfs(graph, 1))
نتيجة:{
0: 2,
1: 0,
2: 1,
3: 3,
4: Infinity
}
هذا كل شيء بالنسبة لي. آمل أن تجد شيئًا مفيدًا لنفسك. الترميز سعيدة!