F # ، خوارزمية وضع العلامات لمكونات الصورة المتصلة

يعد البحث عن المكونات المتصلة ووضع علامة عليها في الصور الثنائية أحد الخوارزميات الأساسية لتحليل الصور ومعالجتها. على وجه الخصوص ، يمكن استخدام هذه الخوارزمية في رؤية الآلة للبحث عن الهياكل الشائعة في الصورة وحسابها ، مع تحليلها اللاحق.

في إطار هذه المقالة ، سيتم النظر في خوارزميتين لتمييز المكونات المتصلة ، ويظهر تنفيذها في لغة البرمجة F #. وأيضًا تحليل مقارن للخوارزميات والبحث عن نقاط الضعف. تم أخذ المواد المصدر لتنفيذ الخوارزميات من كتاب " رؤية الكمبيوتر" (المؤلفان L. Shapiro، J.Stockman. الترجمة من الإنجليزية بواسطة A. A. Boguslavsky تحرير S. M. Sokolov) .

المقدمة

المكون المتصل بقيمة v هو مجموعة من وحدات البكسل C التي لها قيمة v وكل زوج من هذه البكسلات متصل بقيمة v

يبدو مضللاً ، لذا دعنا نرى الصورة فقط. نفترض أن وحدات البكسل الأمامية للصورة الثنائية تم تمييزها على أنها 1 ، وأن بيكسلات الخلفية تم وضع علامة عليها كـ 0 .

بعد معالجة الصورة باستخدام خوارزمية وضع العلامات للمكونات المتصلة ، نحصل على الصورة التالية. هنا ، بدلاً من البكسل ، يتم تكوين المكونات المتصلة ، والتي تختلف عن بعضها البعض في العدد. في هذا المثال ، تم العثور على 5 مكونات وسيكون من الممكن العمل معها كما هو الحال مع كيانات منفصلة.

الشكل 1: المكونات المتصلة المسماة

$$

$$\begin{matrix} 1 & 1 & 0 & 1 & 1 & 1 & 0 & 2 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 & 2 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 \\ 3 & 3 & 3 & 3 & 0 & 4 & 0 & 2 \\ 0 & 0 & 0 & 3 & 0 & 4 & 0 & 2 \\ 5 & 5 & 0 & 3 & 0 & 0 & 0 & 2 \\ 5 & 5 & 0 & 3 & 0 & 2 & 2 & 2 \end{matrix}$$

سيتم النظر في خوارزميتين يمكن استخدامهما لحل هذه المشكلة أدناه.

خوارزمية وضع العلامات العودية

سنبدأ بالنظر إلى الخوارزمية القائمة على العودية باعتبارها الأكثر وضوحًا. سيكون مبدأ تشغيل هذه الخوارزمية على النحو التالي.

قم بتعيين تسمية ، سنقوم بتمييز المكونات ذات الصلة ، القيمة الأولية.

1. نقوم بفرز جميع النقاط في الجدول ، بدءًا بالإحداثيات 0x0 (الزاوية اليسرى العليا). بعد معالجة النقطة التالية ، قم بزيادة التسمية بواحدة
2. إذا كانت البكسل في الإحداثيات الحالية 1 ، فإننا نقوم بمسح جميع الجيران الأربعة لهذه النقطة (أعلى ، أسفل ، يمين ، يسار)
3. إذا كانت النقطة المجاورة هي 1 أيضًا ، فإن الوظيفة تطالب نفسها بشكل متكرر بمعالجة الجار حتى تصل إلى حدود المصفوفة أو النقطة 0
4. أثناء المعالجة العودية للجار ، يجب التحقق من أن النقطة لم يتم معالجتها بالفعل وتم تمييزها بالعلامة الحالية.

وبالتالي ، فرز جميع النقاط في المصفوفة واستدعاء خوارزمية متكررة لكل منها ، ثم في نهاية البحث نحصل على جدول محدد بالكامل. نظرًا لوجود فحص حول ما إذا تم وضع علامة على نقطة معينة بالفعل ، فستتم معالجة كل نقطة مرة واحدة فقط. يعتمد عمق العودية فقط على عدد الجيران المتصلين بالنقطة الحالية. هذه الخوارزمية مناسبة تمامًا للصور التي لا تحتوي على تعبئة صور كبيرة. بمعنى ، الصور التي بها خطوط رقيقة وقصيرة ، وكل شيء آخر هو صورة خلفية لا تتم معالجتها. علاوة على ذلك ، قد تكون سرعة هذه الخوارزمية أعلى من خوارزمية كل سطر على حدة (سنناقشها لاحقًا في المقالة).

نظرًا لأن الصور الثنائية ثنائية الأبعاد هي مصفوفات ثنائية الأبعاد ، فعند كتابة الخوارزمية ، سأعمل مع مفاهيم المصفوفات ، التي قمت من خلالها بعمل مقالة منفصلة ، يمكنك قراءتها هنا.

البرمجة الوظيفية باستخدام مثال العمل مع المصفوفات من نظرية الجبر الخطي.

ضع في اعتبارك وظيفة F # التي تنفذها خوارزمية وضع العلامات العودية لمكونات الصورة الثنائية المتصلة

let recMarkingOfConnectedComponents matrix =

        let copy = Matrix.clone matrix

        let (|Value|Zero|Out|) (x, y) = 
            if x < 0 || y < 0
                || x > (copy.values.[0, *].Length - 1)
                || y > (copy.values.[*, 0].Length - 1) then
                Out
            else
                let row = copy.values.[y, *]
                match row.[x] with
                    | 0 -> Zero
                    | v -> Value(v)

        let rec markBits x y value =
            match (x, y) with
            | Value(v) ->
                if value > v then
                    copy.values.[y, x] <- value
                    markBits (x + 1) y value
                    markBits (x - 1) y value
                    markBits x (y + 1) value
                    markBits x (y - 1) value
            | Zero | Out -> ()

        let mutable value = 2
        copy.values
        |> Array2D.iteri (fun y x v -> if v = 1 then
                                            markBits x y value
                                            value <- value + 1)

        copy 

نعلن وظيفة recMarkingOfConnectedComponents ، التي تأخذ مصفوفة ثنائية الأبعاد من المصفوفة ، معبأة في سجل من نوع المصفوفة. لن تغير الوظيفة الصفيف الأصلي ، لذا قم أولاً بإنشاء نسخة منه ، والتي ستتم معالجتها بواسطة الخوارزمية وإعادتها.

let copy = Matrix.clone matrix

لتبسيط عمليات التحقق من فهارس النقاط المطلوبة خارج الصفيف ، قم بإنشاء قالب نشط يقوم بإرجاع إحدى القيم الثلاث.

خارج - تجاوز الفهرس المطلوب الصفيف ثنائي الأبعاد
Zero - تحتوي النقطة على بكسل خلفية (يساوي صفر)
القيمة - الفهرس المطلوب موجود داخل الصفيف

سيبسط هذا القالب التحقق من إحداثيات نقطة الصورة في إطار العودية التالي:

let (|Value|Zero|Out|) (x, y) = 
    if x < 0 || y < 0
        || x > (copy.values.[0, *].Length - 1)
        || y > (copy.values.[*, 0].Length - 1) then
        Out
    else
        let row = copy.values.[y, *]
        match row.[x] with
            | 0 -> Zero
            | v -> Value(v)

يتم الإعلان عن وظيفة MarkBits عودية وتعمل على معالجة البكسل الحالي وجميع جيرانه (أعلى ، أسفل ، يسار ، يمين):

let rec markBits x y value =
    match (x, y) with
    | Value(v) ->
        if value > v then
            copy.values.[y, x] <- value
            markBits (x + 1) y value
            markBits (x - 1) y value
            markBits x (y + 1) value
            markBits x (y - 1) value
    | Zero | Out -> ()

تقبل الوظيفة المعلمات التالية كمدخل:

x - رقم الصف
y -
قيمة رقم العمود - قيمة التسمية الحالية لوضع علامة على البكسل

باستخدام المطابقة / مع البناء والقالب النشط (أعلاه) ، يتم فحص إحداثيات البكسل بحيث لا تتجاوز الأبعاد الثنائية مجموعة مصفوفة. إذا كانت النقطة داخل مصفوفة ثنائية الأبعاد ، فإننا نقوم بإجراء فحص أولي حتى لا نعالج النقطة التي تمت معالجتها بالفعل.

if value > v then

خلاف ذلك ، سيحدث العودية اللانهائي ولن تعمل الخوارزمية.

بعد ذلك ، ضع علامة على النقطة بقيمة العلامة الحالية:

copy.values.[y, x] <- value

ونعالج جميع جيرانها ، ونطلق على الوظيفة نفسها بشكل متكرر:

markBits (x + 1) y value
markBits (x - 1) y value
markBits x (y + 1) value
markBits x (y - 1) value

بعد تنفيذ الخوارزمية ، يجب استخدامها. ضع في اعتبارك الرمز بمزيد من التفاصيل.

let mutable value = 2
copy.values
|> Array2D.iteri (fun y x v -> if v = 1 then
                                    markBits x y value
                                    value <- value + 1) 

قبل معالجة الصورة ، قم بتعيين القيمة الأولية للملصق ، والتي ستحدد مجموعات وحدات البكسل المتصلة.

let mutable value = 2

والحقيقة هي أن وحدات البكسل الأمامية في الصورة الثنائية قد تم تعيينها بالفعل على 1 ، لذلك إذا كانت القيمة الأولية للملصق هي 1 أيضًا ، فلن تعمل الخوارزمية. لذلك ، يجب أن تكون القيمة الأولية للملصق أكبر من 1 . هناك طريقة أخرى لحل المشكلة. قبل بدء الخوارزمية ، ضع علامة على جميع وحدات البكسل المعينة على 1 بقيمة أولية -1 . ثم يمكننا ضبط القيمة على 1 . يمكنك القيام بذلك بنفسك إذا كنت ترغب في ذلك.

يستخدم البناء التالي وظيفة Array2D.iteri للتكرار عبر جميع النقاط في المصفوفة ، وإذا تم تعيين نقطة على البحث أثناء 1، فهذا يعني أنه لم تتم معالجته ، ومن ثم تحتاج إلى استدعاء markBits للدالة العودية بقيمة التسمية الحالية. يتم تجاهل جميع وحدات البكسل التي تم تعيينها إلى 0 بواسطة الخوارزمية.

بعد معالجة النقطة بشكل متكرر ، يمكننا أن نفترض أن المجموعة المتصلة بالكامل التي تنتمي إليها هذه النقطة مضمونة ، ويمكنك زيادة قيمة التسمية بمقدار 1 لتطبيقها على النقطة المتصلة التالية.

فكر في مثال لتطبيق مثل هذه الخوارزمية.

let a = array2D [[1;1;0;1;1;1;0;1]
                 [1;1;0;1;0;1;0;1]
                 [1;1;1;1;0;0;0;1]
                 [0;0;0;0;0;0;0;1]
                 [1;1;1;1;0;1;0;1]
                 [0;0;0;1;0;1;0;1]
                 [1;1;0;1;0;0;0;1]
                 [1;1;0;1;0;1;1;1]]
let A = Matrix.ofArray2D a

let t = System.Diagnostics.Stopwatch.StartNew()
let R = Algorithms.recMarkingOfConnectedComponents A
t.Stop()

printfn "origin =\n %A" A.values
printfn "rec markers =\n %A" R.values
printfn "elapsed recurcive = %O" t.Elapsed 

origin =
 [[1; 1; 0; 1; 1; 1; 0; 1]
 [1; 1; 0; 1; 0; 1; 0; 1]
 [1; 1; 1; 1; 0; 0; 0; 1]
 [0; 0; 0; 0; 0; 0; 0; 1]
 [1; 1; 1; 1; 0; 1; 0; 1]
 [0; 0; 0; 1; 0; 1; 0; 1]
 [1; 1; 0; 1; 0; 0; 0; 1]
 [1; 1; 0; 1; 0; 1; 1; 1]]

rec markers =
 [[2; 2; 0; 2; 2; 2; 0; 3]
 [2; 2; 0; 2; 0; 2; 0; 3]
 [2; 2; 2; 2; 0; 0; 0; 3]
 [0; 0; 0; 0; 0; 0; 0; 3]
 [4; 4; 4; 4; 0; 5; 0; 3]
 [0; 0; 0; 4; 0; 5; 0; 3]
 [6; 6; 0; 4; 0; 0; 0; 3]
 [6; 6; 0; 4; 0; 3; 3; 3]]

elapsed recurcive = 00:00:00.0037342

تشمل مزايا الخوارزمية العودية بساطتها في الكتابة والفهم. إنه رائع للصور الثنائية التي تحتوي على خلفية كبيرة وتتخللها مجموعات صغيرة من وحدات البكسل (على سبيل المثال ، الخطوط ، والبقع الصغيرة ، وما إلى ذلك). في هذه الحالة ، قد تكون سرعة معالجة الصورة عالية ، حيث تقوم الخوارزمية بمعالجة الصورة بأكملها بتمريرة واحدة.

العيوب واضحة أيضًا - هذا التكرار. إذا كانت الصورة تتكون من بقع كبيرة أو مغمورة تمامًا ، فإن سرعة المعالجة تنخفض بشكل حاد (بأوامر من الحجم) وهناك خطر من تعطل البرنامج على الإطلاق بسبب عدم وجود مساحة خالية على المكدس.

لسوء الحظ ، لا يمكن تطبيق مبدأ العودية الذيل في هذه الخوارزمية ، لأن العودية الذيل لها متطلبان:

1. يجب على كل إطار العودية إجراء العمليات الحسابية وإضافة النتيجة إلى المجمع ، والتي سيتم نقلها إلى أسفل المكدس.
2. يجب ألا يكون هناك أكثر من استدعاء دالة عودي واحد في إطار العودية واحد.

في حالتنا ، لا يقوم العودية بأي حسابات نهائية ، والتي يمكن تمريرها إلى الإطار التالي من العودية ، ولكنها ببساطة تعدل مصفوفة ثنائية الأبعاد. من حيث المبدأ ، يمكن التحايل على هذا بمجرد إرجاع رقم واحد ، وهو في حد ذاته لا يعني أي شيء. نقوم أيضًا بإجراء 4 مكالمات بشكل متكرر ، حيث نحتاج إلى معالجة جميع الجيران الأربعة للنقطة.

الخوارزمية الكلاسيكية لتمييز المكونات المتصلة بناءً على بنية البيانات لدمج عمليات البحث

تحتوي الخوارزمية أيضًا على اسم آخر ، "خوارزمية العلامات التقدمية" ، وهنا سنحاول تحليلها.

. . . , , .

التعريف أعلاه أكثر إرباكًا ، لذلك سنحاول التعامل مع مبدأ الخوارزمية بطريقة مختلفة والبدء من بعيد.

أولا، سنتعامل مع تعريف أربعة - اتصال و ثماني سنوات متصلة حي من النقطة الحالية. انظر إلى الصور أدناه لفهم ما هو وما هو الفرق.

الشكل 2: المكون رباعي التوصيل
\ يبدأ {matrix} الشكل 2: المكون الثماني المتصل \ يبدأ {matrix} تُظهر الصورة الأولى مكونًا رباعي الاتصال $$\begin{matrix} & 1 & \\ 2 & * & 3 \\ & 4 & \end{matrix}$$


$$\begin{matrix} 1 & 2 & 3 \\ 4 & * & 5 \\ 6 & 7 & 8 \end{matrix}$$
أي أن هذا يعني أن الخوارزمية تعالج 4 جيران للنقطة الحالية (يسار ويمين وأعلى وأسفل). وفقًا لذلك ، يعني المكون الثماني المتصل للنقطة أن لديه 8 جيران. في هذه المقالة ، سنعمل مع أربعة مكونات متصلة.

تحتاج الآن إلى معرفة ما هو هيكل البيانات لدمج البحث ، المبني على بعض المجموعات؟

على سبيل المثال ، افترض أن لدينا مجموعتان

$$

$$(1, 2, 3, 4, 8) (5, 6, 7)$$

يتم تنظيم هذه المجموعات على شكل الأشجار التالية: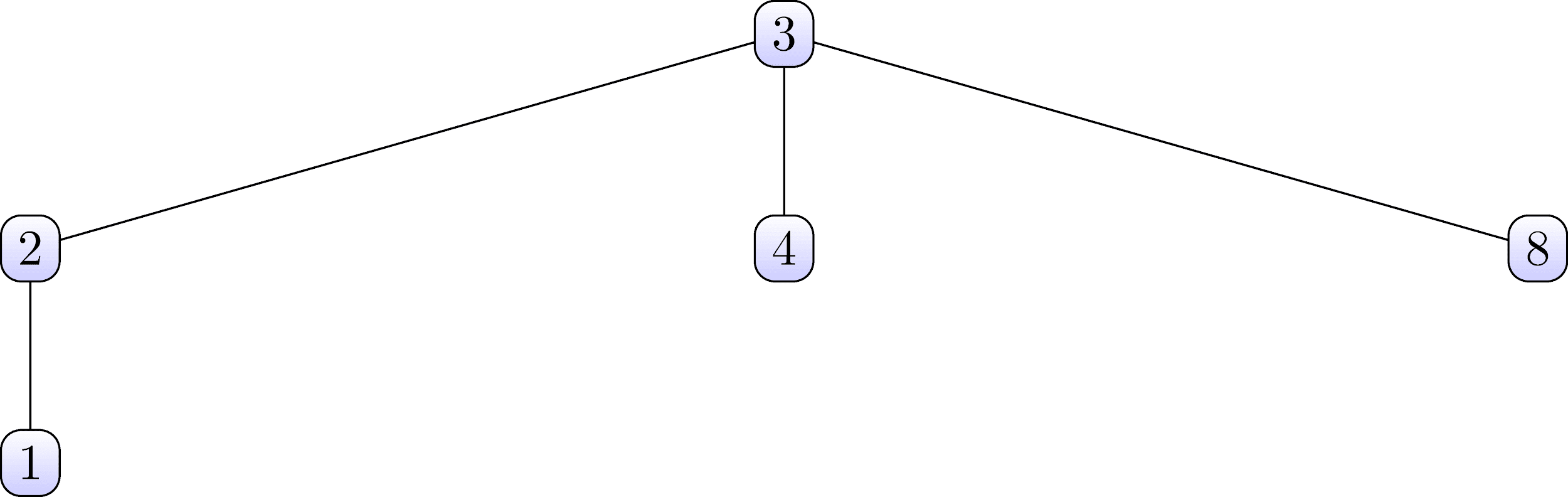





لاحظ أنه في المجموعة الأولى ، تكون العقد 3 هي الجذر ، وفي الثانية العقد 6.

الآن ، نعتبر بنية البيانات لاتحاد البحث ، والتي تحتوي على كلتا المجموعتين ، وننظم أيضًا بنية الشجرة الخاصة بها .

الشكل 4: بنية البيانات لاتحاد البحث
\ تبدأ {matrix} انظر بعناية إلى الجدول أعلاه وحاول إيجاد علاقة مع الأشجار المحددة الموضحة أعلاه. يجب عرض الجدول في أعمدة عمودية. انه مرئي،أن الرقم 3 في السطر الأول يتوافق مع الرقم 0 $$\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 2 & 3 & 0 & 3 & 7 & 7 & 0 & 3 \end{matrix}$$

في السطر الثاني. وفي الشجرة الأولى ، الرقم 3 هو جذر المجموعة الأولى. قياسا على ذلك ، يمكنك أن تجد أن الرقم 7 من السطر الأول يتوافق مع الرقم 0 من السطر الثاني. الرقم 7 هو أيضًا جذر شجرة المجموعة الثانية.

وبالتالي ، نستنتج أن الأرقام من الصف العلوي هي العقد التابعة للمجموعات ، والأرقام المقابلة من الصف السفلي هي العقد الأصلية. تسترشد هذه القاعدة ، يمكنك بسهولة استعادة كلا الشجرتين من الجدول أعلاه.

نقوم بتحليل مثل هذه التفاصيل بحيث يصبح من الأسهل علينا فيما بعد فهم كيفية عمل خوارزمية وضع العلامات التدريجي .. في الوقت الحالي ، دعنا نتحدث عن حقيقة أن سلسلة من الأرقام من الصف الأول هي دائمًا أرقام من 1 إلى حد أقصى معين. في الواقع ، الحد الأقصى لعدد الصف الأول هو الحد الأقصى لقيمة التسميات التي سيتم وضع علامة على المكونات المتصلة الموجودة . والمجموعات الفردية عبارة عن انتقالات بين التسميات التي يتم تشكيلها نتيجة التمرير الأول (سننظر في مزيد من التفاصيل لاحقًا).

قبل المتابعة ، ضع في اعتبارك الرمز الزائف لبعض الوظائف التي ستستخدمها الخوارزمية.

نشير إلى الجدول الذي يمثل بنية البيانات للبحث المشترك باسم PARENT . الوظيفة التالية تسمى Find وستأخذ التسمية X الحالية كمعلماتومجموعة من الوالدين . مؤشرات هذا الإجراء آثار الأم يصل إلى جذر الشجرة ويجد تسمية عقدة جذر الشجرة التي X ينتمي .

 ̆   ̆  .
X —  
PARENT — , ̆    -

procedure find(X, PARENT);
{
j := X;
while PARENT[j] <> 0
    j := PARENT[j]; return(j);
}

ضع في اعتبارك كيف يمكن تنفيذ هذه الوظيفة على F #

let rec find x =
    let index = Array.tryFindIndex ((=)x) parents.[0, *]
    match index with
    | Some(i) -> 
        match parents.[1, i] with
        | p when p <> 0 -> find p
        | _ -> x
    | None -> x 

نحن هنا إعلان وظيفة متكررة من الاكتشاف ، والتي تأخذ التسمية الحالية للX . لا يتم تمرير صفيف PARRENT هنا ، لأننا نمتلكه بالفعل في مساحة الاسم العامة والوظيفة تراه بالفعل ويمكنه العمل معه.

أولاً ، تحاول الوظيفة العثور على فهرس الملصق على السطر العلوي (نظرًا لأنك تحتاج إلى البحث عن أصلها ، الموجود في الخط السفلي.

let index = Array.tryFindIndex ((=)x) parents.[0, *]

إذا نجح البحث ، نحصل على أصله ونقارنه بـ 0 . إذا لم يكن الوالد 0 ، فإن هذه العقدة تحتوي أيضًا على أحد الوالدين والدالة تستدعي نفسها بشكل متكرر حتى يصبح الوالد 0 . هذا يعني أننا وجدنا عقدة الجذر للمجموعة.

match index with
    | Some(i) -> 
        match parents.[1, i] with
        | p when p <> 0 -> find p
        | _ -> x
    | None -> x 

الوظيفة التالية التي نحتاجها تسمى النقابة . يستغرق تسميتين X و Y ، بالإضافة إلى مجموعة من PARENT . هذا الهيكل يعدل (إذا لزم الأمر) الأم الانصهار فرعية تحتوي على تسمية X ، مع مجموعة تضم التسمية Y . يبحث الإجراء عن العقد الجذرية لكلا التصنيفين ، وإذا لم تتطابق ، يتم تعيين عقدة أحد التسميات كعقدة أصل للتسمية الثانية. لذلك هناك اتحاد من مجموعتين.

   .
X — ,   .
Y — ,   .
PARENT — , ̆    -.

procedure union(X, Y, PARENT);
{
j := X;
k := Y;
while PARENT[j] <> 0
    j := PARENT[j];
while PARENT[k]] <> 0
    k := PARENT[k];

if j <> k then PARENT[k] := j;
} 

تنفيذ F # يبدو هكذا

let union x y =
    let j = find x
    let k = find y
    if j <> k then parents.[1, k-1] <- j 

لاحظ أن وظيفة البحث التي قمنا بتنفيذها بالفعل مستخدمة بالفعل هنا .

يتطلب خوارزمية أيضا اثنين من وظائف إضافية، والتي تسمى الدول المجاورة و العلامات . تُرجع وظيفة الجوار مجموعة النقاط المجاورة إلى اليسار والجزء العلوي (حيث تعمل الخوارزمية في حالتنا على مكون رباعي الوصلات) من البكسل المحدد ، وتعيد وظيفة التسميات مجموعة التسميات التي تم تعيينها بالفعل لمجموعة معينة من وحدات البكسل التي أعادتها دالة الجوار . في حالتنا ، لن ننفذ هاتين الوظيفتين ، ولكننا سنقوم بعمل واحدة فقط تجمع بين كل من الوظائف وإرجاع التسميات الموجودة.

let neighbors_labels x y =
    match (x, y) with
    | (0, 0) -> []
    | (0, _) -> [step1.[0, y-1]]
    | (_, 0) -> [step1.[x-1, 0]]
    | _ -> [step1.[x, y-1]; step1.[x-1, y]]
    |> List.filter ((<>)0) 

بالنظر إلى المستقبل ، سأقول على الفور أن المصفوفة step1 التي تستخدم الوظيفة موجودة بالفعل في المساحة العامة وتحتوي على نتيجة معالجة الخوارزمية في التمرير الأول. أريد إيلاء اهتمام خاص لمرشح إضافي.

|> List.filter ((<>)0)

يقطع كل النتائج 0 . أي إذا كان الملصق يحتوي على 0 ، فنحن نتعامل مع نقطة في صورة الخلفية لا تحتاج إلى معالجتها. هذا فارق بسيط مهم للغاية لم يتم ذكره في الكتاب ، والذي نأخذ منه الأمثلة ، ولكن مع ذلك ، لن تعمل الخوارزمية بدون مثل هذا الاختيار.

تدريجياً ، خطوة بخطوة ، نقترب من جوهر الخوارزمية. دعونا ننظر مرة أخرى إلى الصورة التي سنحتاج إلى معالجتها.

الشكل 5: الصورة الثنائية الأصلية
\ تبدأ {matrix} $$\begin{matrix} 1 & 1 & 0 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 & 1 & 1 \end{matrix}$$

قبل المعالجة ، قم بإنشاء مصفوفة فارغة step1 ، حيث سيتم حفظ نتيجة التمرير الأول.

الشكل 6: صفيف الخطوة 1 لتخزين نتائج المعالجة الأساسية
\ ابدأ {matrix} $$\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$

ضع في اعتبارك الخطوات القليلة الأولى لمعالجة البيانات الأولية (فقط الأسطر الثلاثة الأولى من الصورة الثنائية الأصلية).

قبل أن نلقي نظرة على الخوارزمية خطوة بخطوة ، دعنا نلقي نظرة على الكود الزائف الذي يشرح المبدأ العام للتشغيل.

     .
B —   .
LB —   .

procedure classical_with_union-find(B, LB);
{
“  .” initialize();
“  1 ̆  L     .”
for L := 0 to MaxRow
{
“     L  ”
for P := 0 to MaxCol
    LB[L,P] := 0;
“  L.”
for P := 0 to MaxCol
    if B[L,P] == 1 then
    {
        A := prior_neighbors(L,P);
        if isempty(A)
        then {M := label; label := label + 1;};
        else M := min(labels(A));
        LB[L,P] := M;
        for X in labels(A) and X <> M
           union(M, X, PARENT);
    }
}
“  2 ,    1,     .”
for L := 0 to MaxRow
    for P := 0 to MaxCol
        if B[L, P] == 1
        then LB[L,P] := find(LB[L,P], PARENT);
};
      LB ( step1)     ( ).

الشكل 7: الخطوة 1. النقطة (0،0) ، label = 1
\ start {matrix} الشكل 8: الخطوة 2. النقطة (1،0) ، label = 1 \ start {matrix} الشكل 9: الخطوة 2. النقطة (2،0) ، التسمية = 1 \ start {matrix} الشكل 10: الخطوة 4. النقطة (3.0) ، label = 2 \ start {matrix} $$\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$

$$\begin{matrix} 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$

$$\begin{matrix} 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$

$$\begin{matrix} 1 & 1 & 0 & 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$
الشكل 11: الخطوة الأخيرة ، النتيجة النهائية للمرور الأول
\ تبدأ { matrix} لاحظ أنه نتيجة للمعالجة الأولية للصورة الأصلية ، حصلنا على مجموعتين $$\begin{matrix} 1 & 1 & 0 & 2 & 2 & 2 & 0 & 3 \\ 1 & 1 & 0 & 2 & 0 & 2 & 0 & 3 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 \\ 4 & 4 & 4 & 4 & 0 & 5 & 0 & 3 \\ 0 & 0 & 0 & 4 & 0 & 5 & 0 & 3 \\ 6 & 6 & 0 & 4 & 0 & 0 & 0 & 3 \\ 6 & 6 & 0 & 4 & 0 & 7 & 7 & 3 \end{matrix}$$

$$

$$(1,2) - (3,7)$$

بصريا ، يمكن رؤية هذا على أنه اتصال بين العلامة 1 و 2 (إحداثيات النقطتين (1،3) و (2،3) ) والعلامات 3 و 7 (إحداثيات النقاط (7،7) و (7،6) ). من وجهة نظر هيكل البيانات لاتحاد البحث ، يتم الحصول على هذه النتيجة.

الشكل 12: بنية البيانات المحسوبة للانضمام إلى البحث
\ تبدأ {matrix} بعد النهاية معالجة الصور باستخدام بنية البيانات التي تم الحصول عليها ، نحصل على النتيجة التالية. الشكل 13:النتيجة النهائية \ تبدأ {matrix} $$\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 0 & 1 & 0 & 0 & 0 & 0 & 3 \end{matrix}$$



$$\begin{matrix} 1 & 1 & 0 & 1 & 1 & 1 & 0 & 3 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 & 3 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 \\ 4 & 4 & 4 & 4 & 0 & 5 & 0 & 3 \\ 0 & 0 & 0 & 4 & 0 & 5 & 0 & 3 \\ 6 & 6 & 0 & 4 & 0 & 0 & 0 & 3 \\ 6 & 6 & 0 & 4 & 0 & 3 & 3 & 3 \end{matrix}$$
الآن جميع المكونات المتصلة لدينا لدينا تصنيفات فريدة ولها يمكن استخدامها في الخوارزميات اللاحقة للمعالجة.

تنفيذ رمز F # على النحو التالي

let markingOfConnectedComponents matrix =

    // up to 10 markers
    let parents = Array2D.init 2 10 (fun x y -> if x = 0 then y+1 else 0)

    // create a zero initialized copy
    let step1 = (Matrix.cloneO matrix).values

    let rec find x =
        let index = Array.tryFindIndex ((=)x) parents.[0, *]
        match index with
        | Some(i) -> 
            match parents.[1, i] with
            | p when p <> 0 -> find p
            | _ -> x
        | None -> x

    let union x y =
        let j = find x
        let k = find y
        if j <> k then parents.[1, k-1] <- j

    // returns up and left neighbors of pixel
    let neighbors_labels x y =
        match (x, y) with
        | (0, 0) -> []
        | (0, _) -> [step1.[0, y-1]]
        | (_, 0) -> [step1.[x-1, 0]]
        | _ -> [step1.[x, y-1]; step1.[x-1, y]]
        |> List.filter ((<>)0)

    let mutable label = 0
    matrix.values
    |> Array2D.iteri (fun x y v ->
                        if v = 1 then
                            let n = neighbors_labels x y
                            let m = if n.IsEmpty then
                                        label <- label + 1
                                        label
                                    else
                                        n |> List.min
                            n |> List.iter (fun v -> if v <> m then union m v)
                            step1.[x, y] <- m)

    let step2 = matrix.values
                |> Array2D.mapi (fun x y v ->
                        if v = 1 then step1.[x, y] <- find step1.[x, y]
                        step1.[x, y])

    { values = step2 } 

لم يعد تفسير الشفرة سطرا بسطر أي معنى ، حيث تم وصف كل شيء أعلاه. هنا يمكنك ببساطة تعيين رمز F # إلى الرمز الزائف لتوضيح كيفية عمله.

خوارزميات قياس الأداء

دعنا نقارن سرعة معالجة البيانات مع كل من الخوارزميات (العودية والخطيرة).

let a = array2D [[1;1;0;1;1;1;0;1]
                 [1;1;0;1;0;1;0;1]
                 [1;1;1;1;0;0;0;1]
                 [0;0;0;0;0;0;0;1]
                 [1;1;1;1;0;1;0;1]
                 [0;0;0;1;0;1;0;1]
                 [1;1;0;1;0;0;0;1]
                 [1;1;0;1;0;1;1;1]]
let A = Matrix.ofArray2D a

let t1 = System.Diagnostics.Stopwatch.StartNew()
let R1 = Algorithms.markingOfConnectedComponents A
t1.Stop()

let t2 = System.Diagnostics.Stopwatch.StartNew()
let R2 = Algorithms.recMarkingOfConnectedComponents A
t2.Stop()

printfn "origin =\n %A" A.values
printfn "markers =\n %A" R1.values
printfn "rec markers =\n %A" R2.values

printfn "elapsed lines = %O" t1.Elapsed
printfn "elapsed recurcive = %O" t2.Elapsed 

origin =
 [[1; 1; 0; 1; 1; 1; 0; 1]
 [1; 1; 0; 1; 0; 1; 0; 1]
 [1; 1; 1; 1; 0; 0; 0; 1]
 [0; 0; 0; 0; 0; 0; 0; 1]
 [1; 1; 1; 1; 0; 1; 0; 1]
 [0; 0; 0; 1; 0; 1; 0; 1]
 [1; 1; 0; 1; 0; 0; 0; 1]
 [1; 1; 0; 1; 0; 1; 1; 1]]
markers =
 [[1; 1; 0; 1; 1; 1; 0; 3]
 [1; 1; 0; 1; 0; 1; 0; 3]
 [1; 1; 1; 1; 0; 0; 0; 3]
 [0; 0; 0; 0; 0; 0; 0; 3]
 [4; 4; 4; 4; 0; 5; 0; 3]
 [0; 0; 0; 4; 0; 5; 0; 3]
 [6; 6; 0; 4; 0; 0; 0; 3]
 [6; 6; 0; 4; 0; 3; 3; 3]]
rec markers =
 [[2; 2; 0; 2; 2; 2; 0; 3]
 [2; 2; 0; 2; 0; 2; 0; 3]
 [2; 2; 2; 2; 0; 0; 0; 3]
 [0; 0; 0; 0; 0; 0; 0; 3]
 [4; 4; 4; 4; 0; 5; 0; 3]
 [0; 0; 0; 4; 0; 5; 0; 3]
 [6; 6; 0; 4; 0; 0; 0; 3]
 [6; 6; 0; 4; 0; 3; 3; 3]]
elapsed lines = 00:00:00.0081837
elapsed recurcive = 00:00:00.0038338

كما ترى ، في هذا المثال ، تتجاوز سرعة الخوارزمية العودية بشكل كبير سرعة الخوارزمية سطرًا بسطر. لكن كل شيء يتغير بمجرد أن نبدأ في معالجة صورة مليئة بالألوان الصلبة وللتوضيح ، سنقوم أيضًا بزيادة حجمها إلى 100x100 بكسل.

let a = Array2D.create 100 100 1
let A = Matrix.ofArray2D a

let t1 = System.Diagnostics.Stopwatch.StartNew()
let R1 = Algorithms.markingOfConnectedComponents A
t1.Stop()
printfn "elapsed lines = %O" t1.Elapsed

let t2 = System.Diagnostics.Stopwatch.StartNew()
let R2 = Algorithms.recMarkingOfConnectedComponents A
t2.Stop()
printfn "elapsed recurcive = %O" t2.Elapsed 

elapsed lines = 00:00:00.0131790
elapsed recurcive = 00:00:00.2632489

كما ترى ، خوارزمية العودية أبطأ بالفعل 25 مرة من الخوارزمية الخطية. لنقم بزيادة حجم الصورة إلى 200x200 بكسل.

elapsed lines = 00:00:00.0269896
elapsed recurcive = 00:00:06.1033132

الفرق بالفعل مئات المرات. ألاحظ أنه بحجم 300 × 300 بكسل بالفعل ، تتسبب الخوارزمية العودية في تجاوز سعة المكدس وتعطل البرنامج.

ملخص

في إطار هذه المقالة ، تم فحص إحدى الخوارزميات الأساسية لتمييز المكونات المتصلة لمعالجة الصور الثنائية باستخدام اللغة الوظيفية F # كمثال. أعطيت هنا أمثلة على تنفيذ الخوارزميات العودية والكلاسيكية ، وتم شرح مبدأ عملها ، وتم إجراء تحليل مقارن باستخدام أمثلة محددة.

يمكن أيضًا الاطلاع على شفرة المصدر التي تمت مناقشتها هنا في MatrixAlgorithms
github.

آمل أن تكون المقالة مثيرة للاهتمام للمهتمين بـ F # وخوارزميات معالجة الصور على وجه الخصوص.