عندما نأخذ سلسلة كبيرة من اللقطات ، يكون بعضها غامضًا. واجهت شركة سيارات كبيرة نفس المشكلة. بعض الصور أثناء فحص السيارة تبين أنها ضبابية ، مما قد يؤثر سلبًا على المبيعات.
تقلل الصور منخفضة الجودة الأرباح بشكل مباشر.- كيف يتعرف التطبيق على الصور المشوشة على مستوى الخوارزمية؟
- كيف تقيس وضوح صورة RGB؟

صياغة المشكلة
أعمل كمحلل في شركة سيارات كبيرة. عند فحص سيارة ، عند فحص سيارة ، يلتقطون الكثير من الصور من خلال تطبيق خاص ، والتي يتم إرسالها على الفور إلى قاعدة البيانات. بعض الصور ضبابية ، وهو أمر سيئ للمبيعات.من هنا تبرز المشكلة: "كيف تتعرف على الصور الغامضة على مستوى الخوارزمية؟"تم تطوير خوارزمية تستند إلى عينة من 1200 صورة لعناصر مختلفة من السيارات. ميزة العينة هي أنه لم يتم تسميتها ، لأنه من الصعب تحديد الصور الواضحة والأخرى غير الواضحة.اتضح أن تعلم نموذج ML "مع المعلم" لا ينطبق على الحل.أثناء العمل ، استخدمت الأدوات:- بيثون . المكتبات: numpy، matplotlib، cv2؛
- دفتر جوبيتر .
في المقالة سأصف حل المشكلة التي أتيت إليها.وصف نهج حل المشكلة
المرحلة 1. تحديد الحدود
ما الصورة التي يمكن تسميتها واضحة؟واحد يتم فيه تحديد حدود الأشياء. في اللقطات المشوشة ، تكون حدود الكائنات غير واضحة.كيفية تحديد حدود الأشياء في الصورة؟حدود حيث نرى أكبر اختلاف اللون.اتضح أنه لتحديد وضوح الصورة ، تحتاج أولاً إلى تحديد حدود كائنات الصور الفوتوغرافية ، ثم تقييم حجمها وسمكها وعددها ، وما إلى ذلك.تتكون الصورة من مصفوفة ثلاثية الأبعاد للأرقام من 0 إلى 255: (العرض ، الارتفاع ، 3 ألوان).لقد حددت الحدود بتطبيق مرشح كما في إنشاء شبكة عصبية عميقة: بضرب صفيف ثلاثي الأبعاد بالمصفوفات (لكل لون): │ 1 -1 │
│ 1 -1 │
مع اختلاف اللون ، سينتج الصفيف الناتج رقم معامل عالي.لذلك نحدد الحدود الرأسية والأفقية. يُظهر المتوسط الحسابي الحدود المشتركة للصورة.المرحلة 2. تحليل الحدود من أجل الوضوح
يتم تحديد الحدود.كيف تميز حدود الصورة المشوشة عن حدود واضحة؟من خلال الخيارات المختلفة ، وجدت النهج التالي:- تحديد حدود الصورة الأصلية (الموضحة في الخطوة 1) ؛
- طمس الصورة الأصلية ؛
- تحديد حدود الصورة الباهتة (الموضحة في الخطوة 1) ؛
- نعتبر نسبة الوسط الحسابي للفقرة 1 والفقرة 2 ؛
- يميز المعامل الناتج وضوح الصورة.
المنطق بسيط: في الصور الواضحة ، سيحدث التغيير في الحدود بشكل أكثر أهمية من الصور المشوشة ، مما يعني أن المعامل سيكون أعلى.تنفيذ بايثون الخوارزمية
لحل المشكلة مباشرة ، نستخدم المكتبات التالية:import numpy as np
import matplotlib.pyplot as plt
import cv2
من أجل معلمات تحديد الحدود ، نحدد وظيفة تعريف المصفوفة:def edges(n, orient):
edges = np.ones((2*n, 2*n, 3))
if orient == 'vert':
for i in range(0, 2*n):
edges[i][n: 2*n] *= -1
elif orient == 'horiz':
edges[n: 2*n] *= -1
return edges
تحت المعلمة n ، نحدد عدد وحدات البكسل التي نقوم بتضمينها في تقدير الحدود. يمكن أن يكون اتجاه المصفوفة أفقيًا أو رأسيًا.وظائف أخرى تشبه طبقة الشبكة العصبية العميقة:
def conv_single_step(a_slice_prev, W):
s = W * a_slice_prev
Z = np.sum(s)
Z = np.abs(Z)
return Z
def conv_forward(A_prev, W, hparameters):
m = len(A_prev)
(f, f, n_C) = W.shape
stride = hparameters['stride']
pad = hparameters['pad']
Z = list()
flag = 0
z_max = hparameters['z_max']
if len(z_max) == 0:
z_max = list()
flag = 1
for i in range(m):
(x0, x1, x2) = A_prev[i].shape
A_prev_pad = A_prev[i][
int(x0 / 4) : int(x0 * 3 / 4),
int(x1 / 4) : int(x1 * 3 / 4),
:]
(n_H_prev, n_W_prev, n_C_prev) = A_prev_pad.shape
n_H = int((n_H_prev - f + 2*pad) / stride) + 1
n_W = int((n_W_prev - f + 2*pad) / stride) + 1
z = np.zeros((n_H, n_W))
a_prev_pad = A_prev_pad
for h in range(n_H):
vert_start = h * stride
vert_end = h * stride + f
for w in range(n_W):
horiz_start = w * stride
horiz_end = w * stride + f
a_slice_prev = a_prev_pad[vert_start: vert_end, horiz_start: horiz_end, :]
weights = W[:, :, :]
z[h, w] = conv_single_step(a_slice_prev, weights)
if flag == 1:
z_max.append(np.max(z))
Z.append(z / z_max[i])
cache = (A_prev, W, hparameters)
return Z, z_max, cache
def pool_forward(A_prev, hparameters, mode = 'max'):
m = len(A_prev)
f = hparameters['f']
stride = hparameters['stride']
A = list()
for i in range(m):
(n_H_prev, n_W_prev) = A_prev[i].shape
n_H = int(1 + (n_H_prev - f) / stride)
n_W = int(1 + (n_W_prev - f) / stride)
a = np.zeros((n_H, n_W))
for h in range(n_H):
vert_start = h * stride
vert_end = h * stride + f
for w in range(n_W):
horiz_start = w * stride
horiz_end = w * stride + f
a_prev_slice = A_prev[i][vert_start: vert_end, horiz_start: horiz_end]
if mode == 'max':
a[h, w] = np.max(a_prev_slice)
elif mode == 'avg':
a[h, w] = np.mean(a_prev_slice)
A.append(a)
cache = (A_prev, hparameters)
return A, cache
conv_single_step - ضرب واحد لألوان الصورة بواسطة المصفوفات التي تكشف الحدود.conv_forward - تعريف كامل للحدود في الصورة بأكملها.pool_forward - تقليل حجم الصفيف الناتج.بشكل منفصل ، ألاحظ قيمة السطور في الدالة conv_forward:(x0, x1, x2) = A_prev[i].shape
A_prev_pad = A_prev[i][
int(x0 / 4) : int(x0 * 3 / 4),
int(x1 / 4) : int(x1 * 3 / 4),
:]
للتحليل ، نحن لا نستخدم الصورة بأكملها ، ولكن فقط جزءها المركزي ، لأن تركز الكاميرا في كثير من الأحيان على المركز. إذا كانت الصورة واضحة ، فسيكون المركز واضحًا.تحدد الوظيفة التالية حدود الكائنات في الصورة باستخدام الوظائف السابقة:
def borders(images, filter_size = 1, stride = 1, pool_stride = 2, pool_size = 2, z_max = []):
Wv = edges(filter_size, 'vert')
hparameters = {'pad': pad, 'stride': stride, 'pool_stride': pool_stride, 'f': pool_size, 'z_max': z_max}
Z, z_max_v, _ = conv_forward(images, Wv, hparameters)
print('edge filter applied')
hparameters_pool = {'stride': pool_stride, 'f': pool_size}
Av, _ = pool_forward(Z, hparameters_pool, mode = 'max')
print('vertical filter applied')
Wh = edges(filter_size, 'horiz')
hparameters = {'pad': pad, 'stride': stride, 'pool_stride': pool_stride, 'f': pool_size, 'z_max': z_max}
Z, z_max_h, _ = conv_forward(images, Wh, hparameters)
print('edge filter applied')
hparameters_pool = {'stride': pool_stride, 'f': pool_size}
Ah, _ = pool_forward(Z, hparameters_pool, mode = 'max')
print('horizontal filter applied')
return [(Av[i] + Ah[i]) / 2 for i in range(len(Av))], list(map(np.max, zip(z_max_v, z_max_h)))
تحدد الدالة الحدود الرأسية ، ثم الحدود الأفقية ، وترجع الوسط الحسابي لكل من الصفيفين.والوظيفة الرئيسية لإصدار معلمة التعريف:
def orig_blur(images, filter_size = 1, stride = 3, pool_stride = 2, pool_size = 2, blur = 57):
z_max = []
img, z_max = borders(images,
filter_size = filter_size,
stride = stride,
pool_stride = pool_stride,
pool_size = pool_size
)
print('original image borders is calculated')
blurred_img = [cv2.GaussianBlur(x, (blur, blur), 0) for x in images]
print('images blurred')
blurred, z_max = borders(blurred_img,
filter_size = filter_size,
stride = stride,
pool_stride = pool_stride,
pool_size = pool_size,
z_max = z_max
)
print('blurred image borders is calculated')
return [np.mean(orig) / np.mean(blurred) for (orig, blurred) in zip(img, blurred)], img, blurred
أولاً ، نحدد حدود الصورة الأصلية ، ثم نطمس الصورة ، ثم نحدد حدود الصورة الباهتة ، وأخيرًا ، نعتبر نسبة حدود المتوسط الحسابي للصورة الأصلية والتشويش.تعرض الدالة قائمة بعوامل التعريف ، ومجموعة من حدود الصورة الأصلية ومجموعة من حدود التعتيم.مثال على عملية الخوارزمية
للتحليل ، أخذت صور من مخزون الصور freepik.com.


 نحدد حدود الصورة الأولى قبل وبعد التعتيم:
نحدد حدود الصورة الأولى قبل وبعد التعتيم:
 ثانيًا:
ثانيًا:
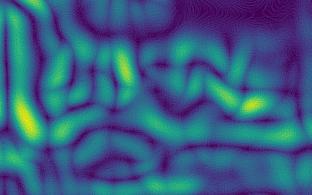 ثالثًا:
ثالثًا:
 رابعًا:
رابعًا:
 في الصور ، يتبين أن تغير الحدود للصور الواضحة (الثالثة والرابعة) أقوى من تلك المشوشة (الأول والثاني).بعد الحسابات نحصل على المعاملات:[5.92918651681958،2.672756123184502،10.695051017699232،11.901115749698139]تؤكد المعاملات الاستنتاجات: كلما كان المعامل أكبر ، كانت الصورة أكثر وضوحًا.علاوة على ذلك ، فإن الصورة الثانية أقل وضوحًا من الصورة الأولى ، والتي تنعكس في المعاملات.
في الصور ، يتبين أن تغير الحدود للصور الواضحة (الثالثة والرابعة) أقوى من تلك المشوشة (الأول والثاني).بعد الحسابات نحصل على المعاملات:[5.92918651681958،2.672756123184502،10.695051017699232،11.901115749698139]تؤكد المعاملات الاستنتاجات: كلما كان المعامل أكبر ، كانت الصورة أكثر وضوحًا.علاوة على ذلك ، فإن الصورة الثانية أقل وضوحًا من الصورة الأولى ، والتي تنعكس في المعاملات.ميزات النهج
- كلما زادت حدة الصورة ، زادت قوة الحدود ، مما يعني ارتفاع المعلمة ؛
- للاحتياجات المختلفة ، هناك حاجة إلى وضوح مختلف. لذلك ، من الضروري تحديد حدود الوضوح بنفسك: في مكان ما ، سيكون معامل الصور الواضحة الكافية أعلى من 7 ، في مكان ما فوق 10 فقط ؛
- يعتمد المعامل على سطوع الصورة. ستتغير حدود الصور المظلمة بشكل أضعف ، مما يعني أن المعامل سيكون أقل. اتضح أنه يجب تحديد حدود الوضوح مع مراعاة الإضاءة ، أي للصور القياسية ؛
يمكن إيجاد خوارزمية عاملة في حسابي على github .