يمكن أن يؤدي وضع التشغيل عن بعد على خلفية العزل الذاتي العالمي إلى عواقب سيئة للغاية. والإرهاق العاطفي - لا يزال أينما ذهب: هناك ، بعد كل شيء ، ليس بعيدًا عن السطح. في هذا الصدد ، مثل الكثيرين ، حاول "تهدئة" نفسه بتخصيص الوقت لفصول أخرى - وبدأ في ترجمة المقالات الأكثر إثارة للاهتمام من الإنجليزية إلى الروسية: "أنت تعطي التعلم الآلي للجماهير!".) يجب أن نشيد: إنه أمر مشتت للانتباه. إذا كانت لديك اقتراحات لكل من المحتوى الدلالي وترجمة هذا النص لقارئ يتحدث الروسية ، انضم إلى المناقشة. إذن ، إليك ترجمة لصفحة التنبؤ بالسلسلة الزمنية من قسم tensorflow اليدوي: الرابط . تهدف الإضافات بالإضافة إلى الرسوم التوضيحية للترجمة إلى المساعدة على فهم الأفكار الأساسية في واحدة من أكثر المجالات إثارة للاهتمام من ML و الاقتصاد القياسي بشكل عام - سلسلة زمنية للتنبؤ.مقدمة صغيرة قبل الترجمة.الدليل هو وصف للتنبؤ بدرجة حرارة الهواء على أساس سلسلة زمنية أحادية البعد ( سلسلة زمنية أحادية المتغير) وسلسلة زمنية متعددة المتغيرات ( سلسلة زمنية متعددة المتغيرات) . لكل جزء ، إدخال البياناتيجب إعدادها وفقًا لذلك. مع مراعاة مجموعة بيانات الأرصاد الجوية التي تم تناولها في هذا الدليل ، يكون الفصل كما يلي:
إذن ، إليك ترجمة لصفحة التنبؤ بالسلسلة الزمنية من قسم tensorflow اليدوي: الرابط . تهدف الإضافات بالإضافة إلى الرسوم التوضيحية للترجمة إلى المساعدة على فهم الأفكار الأساسية في واحدة من أكثر المجالات إثارة للاهتمام من ML و الاقتصاد القياسي بشكل عام - سلسلة زمنية للتنبؤ.مقدمة صغيرة قبل الترجمة.الدليل هو وصف للتنبؤ بدرجة حرارة الهواء على أساس سلسلة زمنية أحادية البعد ( سلسلة زمنية أحادية المتغير) وسلسلة زمنية متعددة المتغيرات ( سلسلة زمنية متعددة المتغيرات) . لكل جزء ، إدخال البياناتيجب إعدادها وفقًا لذلك. مع مراعاة مجموعة بيانات الأرصاد الجوية التي تم تناولها في هذا الدليل ، يكون الفصل كما يلي: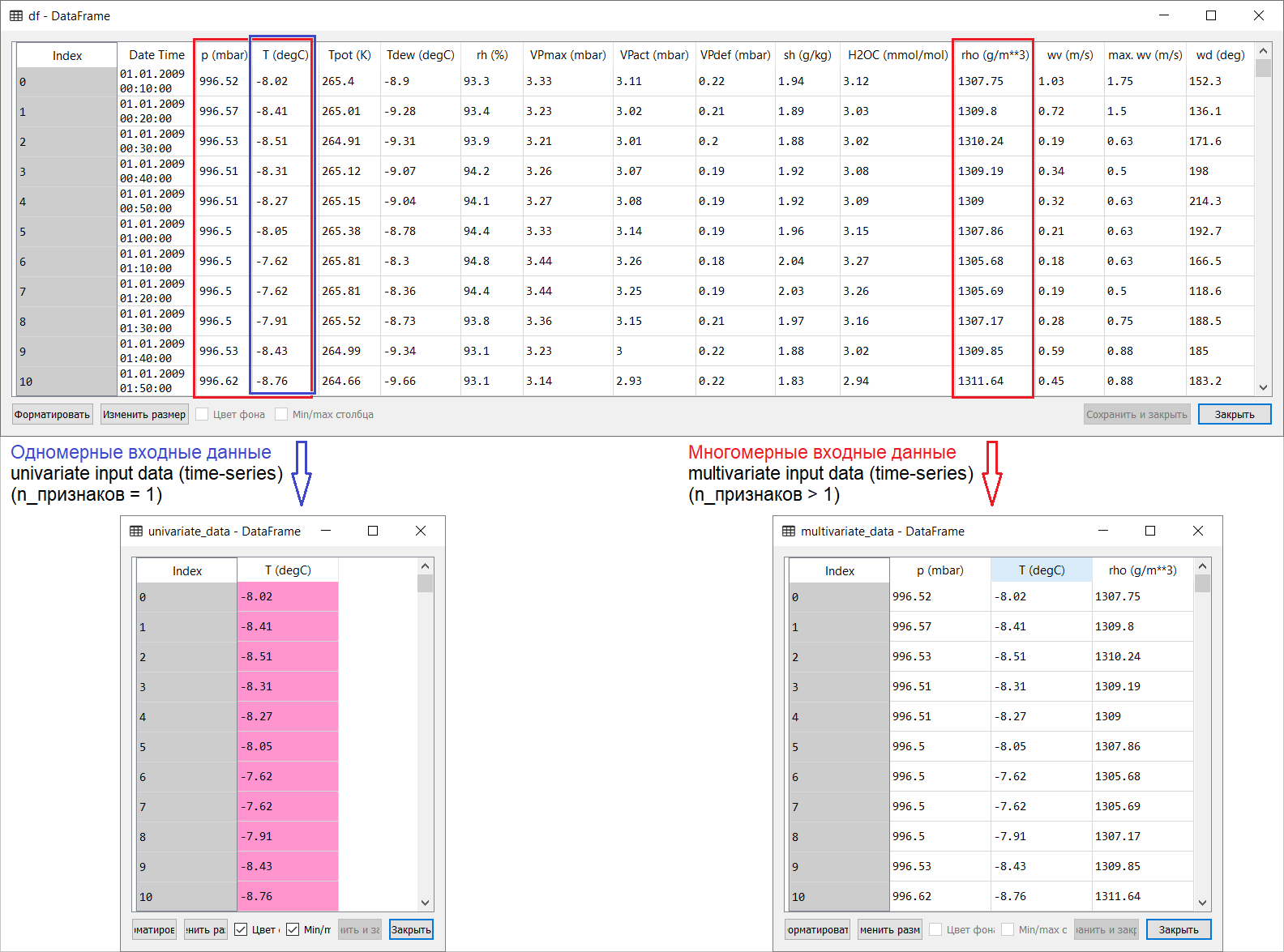 بالنسبة للأسئلة حول ما يجب اتخاذه من X وماذا بالنسبة لـ Y ، أي كيفية إعداد البيانات لفئة التدريب تحت الإشراف ، سيتضح من الرسوم التوضيحية التالية. ألاحظ فقط أن تشكيل المتجه المستهدف (Y) للعمل مع كل من السلاسل الزمنية أحادية البعد والمتعددة الأبعاد هو نفسه: يتم تجميع المتجه الهدف على أساس العلامة T (degC)(درجة حرارة الهواء). الفرق بينهما هو "مدفون" في تشكيل مجموعة من الميزات التي يتم تغذيتها لمدخلات النموذج: في حالة سلسلة زمنية أحادية البعد للتنبؤ بدرجة الحرارة في المستقبل ، يتكون ناقل الإدخال (X) من ميزة واحدة: في الواقع ، درجة حرارة الهواء ؛ ولأبعاد متعددة - أكثر من واحد: بالإضافة إلى درجة حرارة الهواء ، يتم استخدام p (mbar) (الضغط الجوي) و rho (g / m ** 3) (الرطوبة) في مثال الدليل المعني .في البداية ، تبدو نظرة ضحلة بعيدة ، مثال مع التنبؤ بدرجة الحرارة غير مقنع من وجهة نظر استخدام مدخل متعدد الأبعاد: للتنبؤ بدرجة الحرارة ، ستكون العلامة الأكثر صلة هي درجة الحرارة. ومع ذلك ، ليس هذا هو الحال تمامًا: من أجل وضع تنبؤ نوعي لدرجة حرارة الهواء ، يجب مراعاة العديد من العوامل ، حتى احتكاك الهواء على سطح الأرض ، إلخ. بالإضافة إلى ذلك ، من الناحية العملية ، بعض الأشياء بعيدة عن الوضوح ، وقد يكون ناقل الهدف في شكل ذلك المزيج (أو البرش). في هذا الصدد ، فإن تحليل البيانات الاستكشافية مع اختيار السمات الأكثر صلة للتكوين اللاحق لمدخلات متعددة الأبعاد هو القرار الصحيح الوحيد.لذلك ، يتم عرض ترجمة الدليل أدناه. سيكون النص الإضافي مائلًا .
بالنسبة للأسئلة حول ما يجب اتخاذه من X وماذا بالنسبة لـ Y ، أي كيفية إعداد البيانات لفئة التدريب تحت الإشراف ، سيتضح من الرسوم التوضيحية التالية. ألاحظ فقط أن تشكيل المتجه المستهدف (Y) للعمل مع كل من السلاسل الزمنية أحادية البعد والمتعددة الأبعاد هو نفسه: يتم تجميع المتجه الهدف على أساس العلامة T (degC)(درجة حرارة الهواء). الفرق بينهما هو "مدفون" في تشكيل مجموعة من الميزات التي يتم تغذيتها لمدخلات النموذج: في حالة سلسلة زمنية أحادية البعد للتنبؤ بدرجة الحرارة في المستقبل ، يتكون ناقل الإدخال (X) من ميزة واحدة: في الواقع ، درجة حرارة الهواء ؛ ولأبعاد متعددة - أكثر من واحد: بالإضافة إلى درجة حرارة الهواء ، يتم استخدام p (mbar) (الضغط الجوي) و rho (g / m ** 3) (الرطوبة) في مثال الدليل المعني .في البداية ، تبدو نظرة ضحلة بعيدة ، مثال مع التنبؤ بدرجة الحرارة غير مقنع من وجهة نظر استخدام مدخل متعدد الأبعاد: للتنبؤ بدرجة الحرارة ، ستكون العلامة الأكثر صلة هي درجة الحرارة. ومع ذلك ، ليس هذا هو الحال تمامًا: من أجل وضع تنبؤ نوعي لدرجة حرارة الهواء ، يجب مراعاة العديد من العوامل ، حتى احتكاك الهواء على سطح الأرض ، إلخ. بالإضافة إلى ذلك ، من الناحية العملية ، بعض الأشياء بعيدة عن الوضوح ، وقد يكون ناقل الهدف في شكل ذلك المزيج (أو البرش). في هذا الصدد ، فإن تحليل البيانات الاستكشافية مع اختيار السمات الأكثر صلة للتكوين اللاحق لمدخلات متعددة الأبعاد هو القرار الصحيح الوحيد.لذلك ، يتم عرض ترجمة الدليل أدناه. سيكون النص الإضافي مائلًا .التنبؤ بالسلسلة الزمنية
هذا الدليل مقدمة لتنبؤ السلاسل الزمنية باستخدام الشبكات العصبية المتكررة (RNS ، من الشبكة العصبية المتكررة الإنجليزية ، RNN ). يتكون من جزأين: الأول يصف التنبؤ بدرجة حرارة الهواء على أساس سلسلة زمنية أحادية البعد ، والثاني - يعتمد على سلسلة زمنية متعددة الأبعاد.import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
مجموعة من بيانات الأرصاد الجويةجميع الأمثلة على التسلسل الزمني للاستخدام اليدوي لبيانات الطقس المسجلة في محطة الأرصاد الجوية الهيدرولوجية في معهد الكيمياء الحيوية التي سميت باسم ماكس بلانك .تتضمن مجموعة البيانات هذه قياسات لـ 14 مؤشرًا مختلفًا للأرصاد الجوية (مثل درجة حرارة الهواء والضغط الجوي والرطوبة) ، يتم إجراؤها كل 10 دقائق منذ عام 2003. لتوفير الوقت واستخدام الذاكرة ، سيستخدم الدليل بيانات تغطي الفترة من 2009 إلى 2016. أعد هذا القسم من مجموعة البيانات فرانسوا شوليه عن كتابه Deep Learning with Python .zip_path = tf.keras.utils.get_file(
origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
fname='jena_climate_2009_2016.csv.zip',
extract=True)
csv_path, _ = os.path.splitext(zip_path)
df = pd.read_csv(csv_path)
دعونا نرى ما لدينا.df.head()
 يمكن التحقق من حقيقة أن فترة تسجيل الملاحظة 10 دقائق بواسطة الجدول أعلاه. وهكذا ، في ساعة واحدة سيكون لديك 6 ملاحظات. في المقابل ، يتم تجميع 144 (6 × 24) ملاحظة في اليوم.لنفترض أنك تريد التنبؤ بدرجة الحرارة ، التي ستكون في غضون 6 ساعات في المستقبل. تقوم بعمل هذه التوقعات بناءً على البيانات التي لديك لفترة معينة: على سبيل المثال ، تقرر استخدام 5 أيام من المراقبة. لذلك ، لتدريب النموذج ، يجب عليك إنشاء فاصل زمني يحتوي على آخر 720 ملاحظة (5x144) من الملاحظات (نظرًا لأن التكوينات المختلفة ممكنة ، تعد مجموعة البيانات هذه أساسًا جيدًا للتجارب).تعرض الوظيفة أدناه الفترات الزمنية أعلاه لتدريب النموذج. جدال
يمكن التحقق من حقيقة أن فترة تسجيل الملاحظة 10 دقائق بواسطة الجدول أعلاه. وهكذا ، في ساعة واحدة سيكون لديك 6 ملاحظات. في المقابل ، يتم تجميع 144 (6 × 24) ملاحظة في اليوم.لنفترض أنك تريد التنبؤ بدرجة الحرارة ، التي ستكون في غضون 6 ساعات في المستقبل. تقوم بعمل هذه التوقعات بناءً على البيانات التي لديك لفترة معينة: على سبيل المثال ، تقرر استخدام 5 أيام من المراقبة. لذلك ، لتدريب النموذج ، يجب عليك إنشاء فاصل زمني يحتوي على آخر 720 ملاحظة (5x144) من الملاحظات (نظرًا لأن التكوينات المختلفة ممكنة ، تعد مجموعة البيانات هذه أساسًا جيدًا للتجارب).تعرض الوظيفة أدناه الفترات الزمنية أعلاه لتدريب النموذج. جدالhistory_size- هذا هو حجم الفاصل الزمني الأخير ، target_size- حجة تحدد إلى أي مدى يجب أن يتعلم النموذج التنبؤ في المستقبل. بمعنى آخر ، target_sizeهو الناقل المستهدف الذي يجب توقعه.def univariate_data(dataset, start_index, end_index, history_size, target_size):
data = []
labels = []
start_index = start_index + history_size
if end_index is None:
end_index = len(dataset) - target_size
for i in range(start_index, end_index):
indices = range(i-history_size, i)
data.append(np.reshape(dataset[indices], (history_size, 1)))
labels.append(dataset[i+target_size])
return np.array(data), np.array(labels)
في جزأي الدليل ، سيتم استخدام أول 300000 صف من البيانات لتدريب النموذج ، والباقي للتحقق من صحة (التحقق). في هذه الحالة ، يكون مقدار بيانات التدريب 2100 يومًا تقريبًا.TRAIN_SPLIT = 300000
لضمان نتائج قابلة للتكرار ، يتم تعيين وظيفة البذور.tf.random.set_seed(13)
الجزء 1. التنبؤ على أساس سلسلة زمنية أحادية البعد
في الجزء الأول ، ستقوم بتدريب النموذج باستخدام سمة واحدة فقط - درجة الحرارة ؛ سيتم استخدام النموذج المدرب للتنبؤ بدرجات الحرارة المستقبلية.للبدء ، نستخرج فقط درجة الحرارة من مجموعة البيانات.uni_data = df['T (degC)']
uni_data.index = df['Date Time']
uni_data.head()
Date Time
01.01.2009 00:10:00 -8.02
01.01.2009 00:20:00 -8.41
01.01.2009 00:30:00 -8.51
01.01.2009 00:40:00 -8.31
01.01.2009 00:50:00 -8.27
Name: T (degC), dtype: float64
ودعنا نرى كيف تتغير هذه البيانات بمرور الوقت.uni_data.plot(subplots=True)

uni_data = uni_data.values
قبل تدريب شبكة عصبية اصطناعية (من الآن فصاعدًا - ANN) ، فإن خطوة مهمة هي تحجيم البيانات. يعد التوحيد القياسي ( التوحيد ) أحد الطرق الشائعة لإجراء القياس ، ويتم ذلك عن طريق طرح المتوسط والانقسام بواسطة الانحراف المعياري لكل خاصية. يمكنك أيضًا استخدام طريقة tf.keras.utils.normalizeتحجيم القيم إلى النطاق [0،1].ملاحظة : يجب أن يتم التقييس باستخدام بيانات التدريب فقط.uni_train_mean = uni_data[:TRAIN_SPLIT].mean()
uni_train_std = uni_data[:TRAIN_SPLIT].std()
نقوم بتوحيد البيانات.uni_data = (uni_data-uni_train_mean)/uni_train_std
بعد ذلك ، سنقوم بإعداد البيانات للنموذج بإدخال أحادي البعد. سيتم تغذية آخر 20 ملاحظة مسجلة لدرجة الحرارة إلى مدخل النموذج ، ويجب تدريب النموذج على التنبؤ بدرجة الحرارة في الخطوة الزمنية التالية.univariate_past_history = 20
univariate_future_target = 0
x_train_uni, y_train_uni = univariate_data(uni_data, 0, TRAIN_SPLIT,
univariate_past_history,
univariate_future_target)
x_val_uni, y_val_uni = univariate_data(uni_data, TRAIN_SPLIT, None,
univariate_past_history,
univariate_future_target)
نتائج تطبيق الوظيفة univariate_data.print ('Single window of past history')
print (x_train_uni[0])
print ('\n Target temperature to predict')
print (y_train_uni[0])
Single window of past history
[[-1.99766294]
[-2.04281897]
[-2.05439744]
[-2.0312405 ]
[-2.02660912]
[-2.00113649]
[-1.95134907]
[-1.95134907]
[-1.98492663]
[-2.04513467]
[-2.08334362]
[-2.09723778]
[-2.09376424]
[-2.09144854]
[-2.07176515]
[-2.07176515]
[-2.07639653]
[-2.08913285]
[-2.09260639]
[-2.10418486]]
Target temperature to predict
-2.1041848598100876
بالإضافة إلى ذلك: يتم عرض إعداد البيانات لنموذج مع إدخال أحادي البعد بشكل تخطيطي في الشكل التالي (للراحة ، في هذا الشكل والأشكال اللاحقة ، يتم تقديم البيانات في شكل "خام" ، قبل التوحيد القياسي ، وأيضًا بدون السمة "وقت التاريخ" كمؤشر): الآن بعد أن البيانات أعد على النحو المناسب ، والنظر في مثال ملموس. يتم تمييز المعلومات المرسلة إلى ANN باللون الأزرق ، ويشير الصليب الأحمر إلى القيمة المستقبلية التي يجب أن تتوقعها ANN.
الآن بعد أن البيانات أعد على النحو المناسب ، والنظر في مثال ملموس. يتم تمييز المعلومات المرسلة إلى ANN باللون الأزرق ، ويشير الصليب الأحمر إلى القيمة المستقبلية التي يجب أن تتوقعها ANN.def create_time_steps(length):
return list(range(-length, 0))
def show_plot(plot_data, delta, title):
labels = ['History', 'True Future', 'Model Prediction']
marker = ['.-', 'rx', 'go']
time_steps = create_time_steps(plot_data[0].shape[0])
if delta:
future = delta
else:
future = 0
plt.title(title)
for i, x in enumerate(plot_data):
if i:
plt.plot(future, plot_data[i], marker[i], markersize=10,
label=labels[i])
else:
plt.plot(time_steps, plot_data[i].flatten(), marker[i], label=labels[i])
plt.legend()
plt.xlim([time_steps[0], (future+5)*2])
plt.xlabel('Time-Step')
return plt
show_plot([x_train_uni[0], y_train_uni[0]], 0, 'Sample Example')
 الحل الأساسي (بدون إشراك التعلم الآلي)قبل بدء تدريب النموذج ، سنقوم بتثبيت حل أساسي بسيط ( خط الأساس ). وتتكون من التالي: بالنسبة لمتجه إدخال معين ، فإن طريقة الحل الأساسية "تفحص" التاريخ بأكمله وتتنبأ بالقيمة التالية كمتوسط لآخر 20 ملاحظة.
الحل الأساسي (بدون إشراك التعلم الآلي)قبل بدء تدريب النموذج ، سنقوم بتثبيت حل أساسي بسيط ( خط الأساس ). وتتكون من التالي: بالنسبة لمتجه إدخال معين ، فإن طريقة الحل الأساسية "تفحص" التاريخ بأكمله وتتنبأ بالقيمة التالية كمتوسط لآخر 20 ملاحظة.def baseline(history):
return np.mean(history)
show_plot([x_train_uni[0], y_train_uni[0], baseline(x_train_uni[0])], 0,
'Baseline Prediction Example')
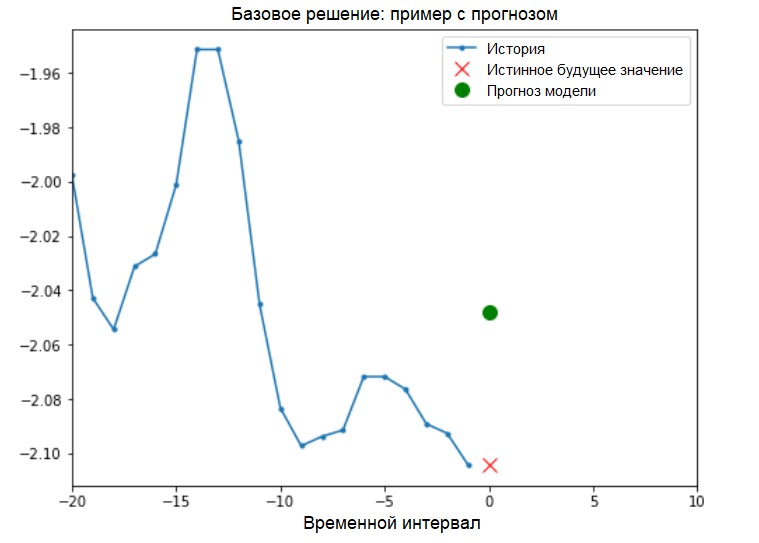 دعونا نرى ما إذا كان بإمكاننا تجاوز نتيجة "المتوسط" باستخدام شبكة عصبية متكررة.الشبكة العصبية المتكررة تعتبر الشبكة العصبيةالمتكررة (RNS) نوعًا من ANN مناسب تمامًا لحل مشكلات السلاسل الزمنية. تقوم RNS خطوة بخطوة بمعالجة التسلسل الزمني للبيانات ، وفرز عناصرها والحفاظ على الحالة الداخلية التي تم الحصول عليها عن طريق معالجة العناصر السابقة. يمكنك العثور على مزيد من المعلومات حول RNS في الدليل التالي . سيستخدم هذا الدليل طبقة متخصصة من RNC تسمى الذاكرة طويلة المدى ( LSTM ).مزيد من استخدام
دعونا نرى ما إذا كان بإمكاننا تجاوز نتيجة "المتوسط" باستخدام شبكة عصبية متكررة.الشبكة العصبية المتكررة تعتبر الشبكة العصبيةالمتكررة (RNS) نوعًا من ANN مناسب تمامًا لحل مشكلات السلاسل الزمنية. تقوم RNS خطوة بخطوة بمعالجة التسلسل الزمني للبيانات ، وفرز عناصرها والحفاظ على الحالة الداخلية التي تم الحصول عليها عن طريق معالجة العناصر السابقة. يمكنك العثور على مزيد من المعلومات حول RNS في الدليل التالي . سيستخدم هذا الدليل طبقة متخصصة من RNC تسمى الذاكرة طويلة المدى ( LSTM ).مزيد من استخدامtf.dataخلط مجموعة البيانات وتجميعها وتخزينها مؤقتًا.إضافة:
مزيد من المعلومات حول طرق الخلط والدُفعة وذاكرة التخزين المؤقت في صفحة tensorflow :BATCH_SIZE = 256
BUFFER_SIZE = 10000
train_univariate = tf.data.Dataset.from_tensor_slices((x_train_uni, y_train_uni))
train_univariate = train_univariate.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
val_univariate = tf.data.Dataset.from_tensor_slices((x_val_uni, y_val_uni))
val_univariate = val_univariate.batch(BATCH_SIZE).repeat()
من المفترض أن يساعدك التمثيل البصري التالي في فهم شكل البيانات بعد المعالجة المجمعة. يمكن ملاحظة أن LSTM يتطلب نوعًا معينًا من إدخال البيانات ، والذي يتم توفيره له.
يمكن ملاحظة أن LSTM يتطلب نوعًا معينًا من إدخال البيانات ، والذي يتم توفيره له.simple_lstm_model = tf.keras.models.Sequential([
tf.keras.layers.LSTM(8, input_shape=x_train_uni.shape[-2:]),
tf.keras.layers.Dense(1)
])
simple_lstm_model.compile(optimizer='adam', loss='mae')
تحقق من إخراج النموذج.for x, y in val_univariate.take(1):
print(simple_lstm_model.predict(x).shape)
(256, 1)
إضافة:
بشكل عام ، تعمل RNS مع التسلسل. هذا يعني أن البيانات المقدمة لمدخلات النموذج يجب أن يكون لها الشكل التالي:
[, , - ]
نموذج بيانات التدريب للنموذج مع إدخال أحادي البعد لديه الشكل التالي:print(x_train_uni.shape)
(299980, 20, 1)بعد ذلك ، سوف ندرس النموذج. نظرًا للحجم الكبير لمجموعة البيانات ومن أجل توفير الوقت ، ستمر كل حقبة بـ 200 خطوة فقط ( steps_per_epoch = 200 ) بدلاً من بيانات التدريب الكاملة ، كما يحدث عادةً.EVALUATION_INTERVAL = 200
EPOCHS = 10
simple_lstm_model.fit(train_univariate, epochs=EPOCHS,
steps_per_epoch=EVALUATION_INTERVAL,
validation_data=val_univariate, validation_steps=50)
Train for 200 steps, validate for 50 steps
Epoch 1/10
200/200 [==============================] - 2s 11ms/step - loss: 0.4075 - val_loss: 0.1351
Epoch 2/10
200/200 [==============================] - 1s 4ms/step - loss: 0.1118 - val_loss: 0.0360
Epoch 3/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0490 - val_loss: 0.0289
Epoch 4/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0444 - val_loss: 0.0257
Epoch 5/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0299 - val_loss: 0.0235
Epoch 6/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0317 - val_loss: 0.0224
Epoch 7/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0287 - val_loss: 0.0206
Epoch 8/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0263 - val_loss: 0.0200
Epoch 9/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0254 - val_loss: 0.0182
Epoch 10/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0228 - val_loss: 0.0174
التنبؤ باستخدام نموذج LSTM بسيطبعد الانتهاء من إعداد نموذج LSTM بسيط ، سنقوم بعمل العديد من التنبؤات.for x, y in val_univariate.take(3):
plot = show_plot([x[0].numpy(), y[0].numpy(),
simple_lstm_model.predict(x)[0]], 0, 'Simple LSTM model')
plot.show()
 يبدو أفضل من المستوى الأساسي.الآن بعد أن أصبحت على دراية بالأساسيات ، دعنا ننتقل إلى الجزء الثاني ، الذي يصف العمل مع سلسلة زمنية متعددة الأبعاد.
يبدو أفضل من المستوى الأساسي.الآن بعد أن أصبحت على دراية بالأساسيات ، دعنا ننتقل إلى الجزء الثاني ، الذي يصف العمل مع سلسلة زمنية متعددة الأبعاد.الجزء 2: التنبؤ بالسلسلة الزمنية متعددة الأبعاد
كما ذكر ، تحتوي مجموعة البيانات الأصلية على 14 مؤشرًا مختلفًا للأرصاد الجوية. من أجل البساطة والراحة ، في الجزء الثاني فقط ثلاثة منها - درجة حرارة الهواء والضغط الجوي وكثافة الهواء.لاستخدام المزيد من الميزات ، يجب إضافة أسمائهم إلى قائمة feature_consosed .features_considered = ['p (mbar)', 'T (degC)', 'rho (g/m**3)']
features = df[features_considered]
features.index = df['Date Time']
features.head()
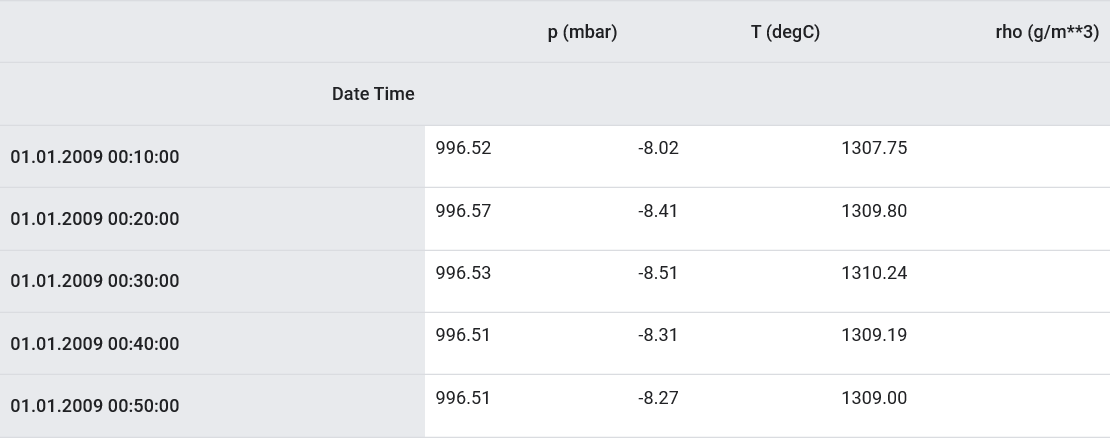 دعونا نرى كيف تتغير هذه المؤشرات بمرور الوقت.
دعونا نرى كيف تتغير هذه المؤشرات بمرور الوقت.features.plot(subplots=True)
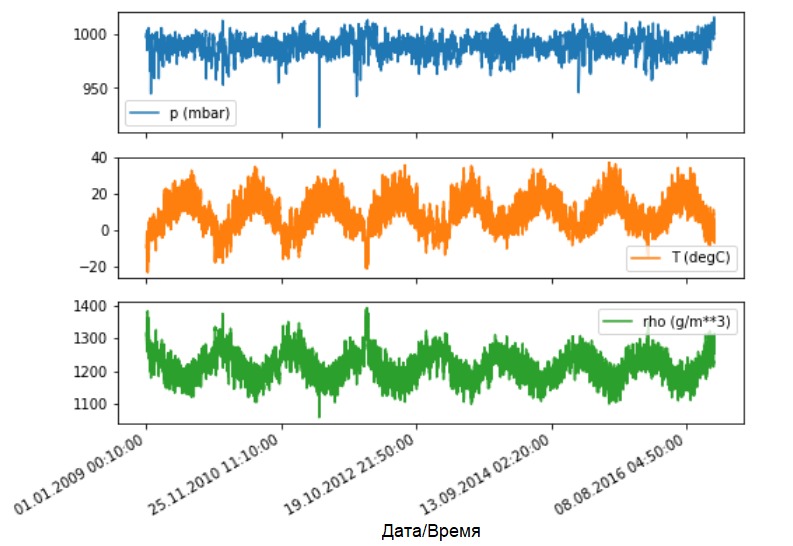 كما كان من قبل ، فإن الخطوة الأولى هي توحيد مجموعة البيانات مع حساب متوسط القيمة والانحراف المعياري لبيانات التدريب.
كما كان من قبل ، فإن الخطوة الأولى هي توحيد مجموعة البيانات مع حساب متوسط القيمة والانحراف المعياري لبيانات التدريب.dataset = features.values
data_mean = dataset[:TRAIN_SPLIT].mean(axis=0)
data_std = dataset[:TRAIN_SPLIT].std(axis=0)
dataset = (dataset-data_mean)/data_std
إضافة:
سنتحدث أكثر في الدليل عن التنبؤ بالنقاط والفواصل الزمنية.
خلاصة القول هي على النحو التالي. إذا كنت بحاجة إلى النموذج للتنبؤ بقيمة واحدة في المستقبل (على سبيل المثال ، قيمة درجة الحرارة بعد 12 ساعة) (نموذج من خطوة واحدة / خطوة واحدة) ، فيجب عليك تدريب النموذج بحيث يتنبأ بقيمة واحدة فقط في المستقبل. إذا كانت المهمة هي التنبؤ بنطاق القيم في المستقبل (على سبيل المثال ، درجات الحرارة لكل ساعة خلال الـ 12 ساعة القادمة) (نموذج متعدد الخطوات) ، فيجب تدريب النموذج أيضًا على التنبؤ بنطاق القيم في المستقبل. التنبؤ بالنقاطفي هذه الحالة ، يتم تدريب النموذج على توقع قيمة واحدة في المستقبل بناءً على بعض التاريخ المتاح.تقوم الوظيفة أدناه بتنفيذ نفس المهمة المتمثلة في تنظيم الفترات الزمنية فقط مع الاختلاف الذي تحدده هنا أحدث الملاحظات بناءً على حجم خطوة معين.
التنبؤ بالنقاطفي هذه الحالة ، يتم تدريب النموذج على توقع قيمة واحدة في المستقبل بناءً على بعض التاريخ المتاح.تقوم الوظيفة أدناه بتنفيذ نفس المهمة المتمثلة في تنظيم الفترات الزمنية فقط مع الاختلاف الذي تحدده هنا أحدث الملاحظات بناءً على حجم خطوة معين.def multivariate_data(dataset, target, start_index, end_index, history_size,
target_size, step, single_step=False):
data = []
labels = []
start_index = start_index + history_size
if end_index is None:
end_index = len(dataset) - target_size
for i in range(start_index, end_index):
indices = range(i-history_size, i, step)
data.append(dataset[indices])
if single_step:
labels.append(target[i+target_size])
else:
labels.append(target[i:i+target_size])
return np.array(data), np.array(labels)
في هذا الدليل ، يعمل ANN على بيانات لآخر خمسة (5) أيام ، أي 720 ملاحظة (6 × 24 × 5). افترض أن اختيار البيانات لا يتم كل 10 دقائق ، ولكن كل ساعة: في غضون 60 دقيقة ، لا يتوقع حدوث تغييرات حادة. لذلك ، فإن تاريخ الأيام الخمسة الأخيرة يتكون من 120 ملاحظة (720/6). بالنسبة للنموذج الذي يقوم بالتنبؤ الموضعي ، فإن الهدف هو قراءة درجة الحرارة بعد 12 ساعة في المستقبل. في هذه الحالة ، سيكون المتجه المستهدف هو درجة الحرارة بعد 72 ملاحظة (12 × 6) ( انظر الإضافة التالية - المترجم التقريبي ).past_history = 720
future_target = 72
STEP = 6
x_train_single, y_train_single = multivariate_data(dataset, dataset[:, 1], 0,
TRAIN_SPLIT, past_history,
future_target, STEP,
single_step=True)
x_val_single, y_val_single = multivariate_data(dataset, dataset[:, 1],
TRAIN_SPLIT, None, past_history,
future_target, STEP,
single_step=True)
تحقق من الفاصل الزمني.print ('Single window of past history : {}'.format(x_train_single[0].shape))
Single window of past history : (120, 3)
train_data_single = tf.data.Dataset.from_tensor_slices((x_train_single, y_train_single))
train_data_single = train_data_single.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
val_data_single = tf.data.Dataset.from_tensor_slices((x_val_single, y_val_single))
val_data_single = val_data_single.batch(BATCH_SIZE).repeat()
single_step_model = tf.keras.models.Sequential()
single_step_model.add(tf.keras.layers.LSTM(32,
input_shape=x_train_single.shape[-2:]))
single_step_model.add(tf.keras.layers.Dense(1))
single_step_model.compile(optimizer=tf.keras.optimizers.RMSprop(), loss='mae')
سوف نتحقق من العينة ونشتق منحنيات الخسارة في مراحل التدريب والتحقق.for x, y in val_data_single.take(1):
print(single_step_model.predict(x).shape)
(256, 1)
single_step_history = single_step_model.fit(train_data_single, epochs=EPOCHS,
steps_per_epoch=EVALUATION_INTERVAL,
validation_data=val_data_single,
validation_steps=50)
Train for 200 steps, validate for 50 steps
Epoch 1/10
200/200 [==============================] - 4s 18ms/step - loss: 0.3090 - val_loss: 0.2646
Epoch 2/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2624 - val_loss: 0.2435
Epoch 3/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2616 - val_loss: 0.2472
Epoch 4/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2567 - val_loss: 0.2442
Epoch 5/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2263 - val_loss: 0.2346
Epoch 6/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2416 - val_loss: 0.2643
Epoch 7/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2411 - val_loss: 0.2577
Epoch 8/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2410 - val_loss: 0.2388
Epoch 9/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2447 - val_loss: 0.2485
Epoch 10/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2388 - val_loss: 0.2422
def plot_train_history(history, title):
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(loss))
plt.figure()
plt.plot(epochs, loss, 'b', label='Training loss')
plt.plot(epochs, val_loss, 'r', label='Validation loss')
plt.title(title)
plt.legend()
plt.show()
plot_train_history(single_step_history,
'Single Step Training and validation loss')
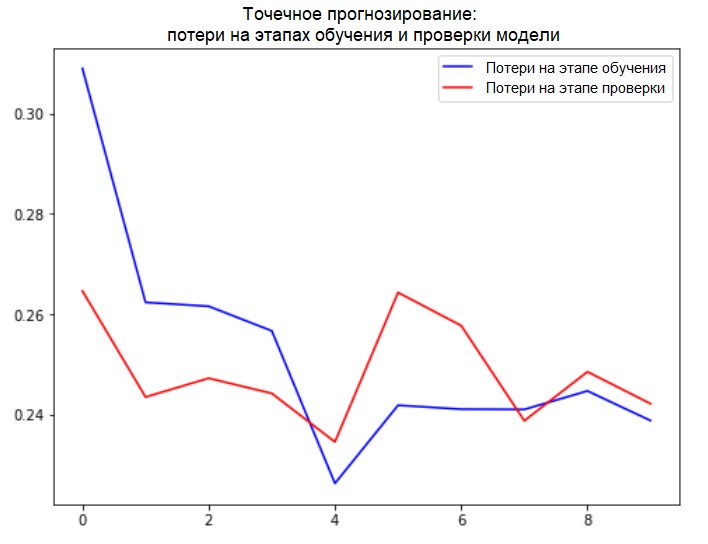 إضافة: يتم عرض
إضافة: يتم عرض
إعداد البيانات لنموذج ذي تنبؤ نقطة إدخال متعدد الأبعاد بشكل تخطيطي في الشكل التالي. من أجل الراحة وتمثيل أكثر وضوحًا لإعداد البيانات ، فإن الحجة STEPهي 1. لاحظ أنه في وظائف المولد المحددة ، فإن الحجة STEP مخصصة فقط لتشكيل التاريخ ، وليس للمتجه المستهدف.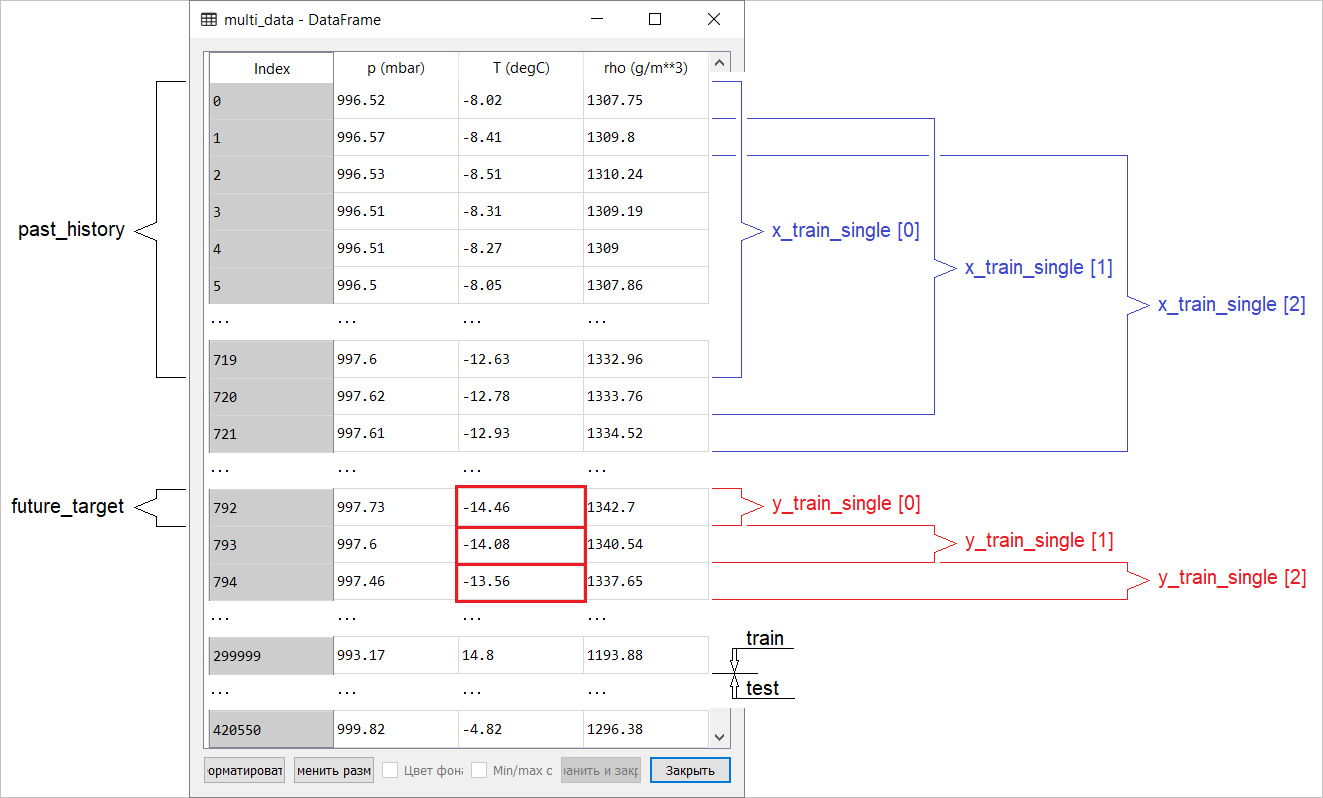 في هذه الحالة ،
في هذه الحالة ، x_train_singleلديها الشكل (299280, 720, 3).
متى STEP=6، سيأخذ النموذج الشكل التالي: (299280, 120, 3)وستزداد سرعة الوظيفة بشكل ملحوظ. بشكل عام ، تحتاج إلى منح الفضل للمبرمج: المولدات المقدمة في الدليل شديدة الشفقة من حيث استهلاك الذاكرة.إجراء تنبؤ بالنقطةالآن بعد أن تم تدريب النموذج ، سنجري العديد من تنبؤات الاختبار. يتم تغذية سجل ملاحظات 3 إشارات للأيام الخمسة الأخيرة ، التي يتم تحديدها كل ساعة (الفاصل الزمني = 120) ، بإدخال النموذج. نظرًا لأن هدفنا هو التنبؤ بدرجة الحرارة فقط ، يتم عرض قيم درجة الحرارة السابقة ( التاريخ ) باللون الأزرق على الرسم البياني . تم عمل التوقعات لمدة نصف يوم في المستقبل (وبالتالي الفجوة بين التاريخ والقيمة المتوقعة).for x, y in val_data_single.take(3):
plot = show_plot([x[0][:, 1].numpy(), y[0].numpy(),
single_step_model.predict(x)[0]], 12,
'Single Step Prediction')
plot.show()
 التنبؤ بالفاصل الزمنيفي هذه الحالة ، على أساس بعض التاريخ المتاح ، يتم تدريب النموذج على التنبؤ بفاصل القيم المستقبلية. وبالتالي ، على عكس النموذج الذي يتنبأ بقيمة واحدة فقط في المستقبل ، فإن هذا النموذج يتنبأ بسلسلة من القيم في المستقبل.لنفترض ، كما في حالة التنبؤ بنقطة أداء النموذج ، بالنسبة للتنبؤ بالفاصل الزمني للنموذج ، أن بيانات التدريب هي قياسات كل ساعة لآخر خمسة أيام (720/6). ومع ذلك ، في هذه الحالة ، يجب تدريب النموذج على التنبؤ بدرجة الحرارة خلال الـ 12 ساعة القادمة. نظرًا لأن الملاحظات يتم تسجيلها كل 10 دقائق ، يجب أن يتكون ناتج النموذج من 72 توقعًا. لإكمال هذه المهمة ، من الضروري إعداد مجموعة البيانات مرة أخرى ، ولكن بفاصل زمني هدف مختلف.
التنبؤ بالفاصل الزمنيفي هذه الحالة ، على أساس بعض التاريخ المتاح ، يتم تدريب النموذج على التنبؤ بفاصل القيم المستقبلية. وبالتالي ، على عكس النموذج الذي يتنبأ بقيمة واحدة فقط في المستقبل ، فإن هذا النموذج يتنبأ بسلسلة من القيم في المستقبل.لنفترض ، كما في حالة التنبؤ بنقطة أداء النموذج ، بالنسبة للتنبؤ بالفاصل الزمني للنموذج ، أن بيانات التدريب هي قياسات كل ساعة لآخر خمسة أيام (720/6). ومع ذلك ، في هذه الحالة ، يجب تدريب النموذج على التنبؤ بدرجة الحرارة خلال الـ 12 ساعة القادمة. نظرًا لأن الملاحظات يتم تسجيلها كل 10 دقائق ، يجب أن يتكون ناتج النموذج من 72 توقعًا. لإكمال هذه المهمة ، من الضروري إعداد مجموعة البيانات مرة أخرى ، ولكن بفاصل زمني هدف مختلف.future_target = 72
x_train_multi, y_train_multi = multivariate_data(dataset, dataset[:, 1], 0,
TRAIN_SPLIT, past_history,
future_target, STEP)
x_val_multi, y_val_multi = multivariate_data(dataset, dataset[:, 1],
TRAIN_SPLIT, None, past_history,
future_target, STEP)
تحقق من الاختيار.print ('Single window of past history : {}'.format(x_train_multi[0].shape))
print ('\n Target temperature to predict : {}'.format(y_train_multi[0].shape))
Single window of past history : (120, 3)
Target temperature to predict : (72,)
train_data_multi = tf.data.Dataset.from_tensor_slices((x_train_multi, y_train_multi))
train_data_multi = train_data_multi.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
val_data_multi = tf.data.Dataset.from_tensor_slices((x_val_multi, y_val_multi))
val_data_multi = val_data_multi.batch(BATCH_SIZE).repeat()
إضافة: يظهر الفرق في تكوين متجه الهدف لـ "النموذج الفاصل" من "النموذج النقطي" في الشكل التالي. سنقوم بإعداد التصور.
سنقوم بإعداد التصور.def multi_step_plot(history, true_future, prediction):
plt.figure(figsize=(12, 6))
num_in = create_time_steps(len(history))
num_out = len(true_future)
plt.plot(num_in, np.array(history[:, 1]), label='History')
plt.plot(np.arange(num_out)/STEP, np.array(true_future), 'bo',
label='True Future')
if prediction.any():
plt.plot(np.arange(num_out)/STEP, np.array(prediction), 'ro',
label='Predicted Future')
plt.legend(loc='upper left')
plt.show()
في هذا الرسم البياني والمخططات اللاحقة المشابهة ، يكون التاريخ والبيانات المستقبلية كل ساعة.for x, y in train_data_multi.take(1):
multi_step_plot(x[0], y[0], np.array([0]))
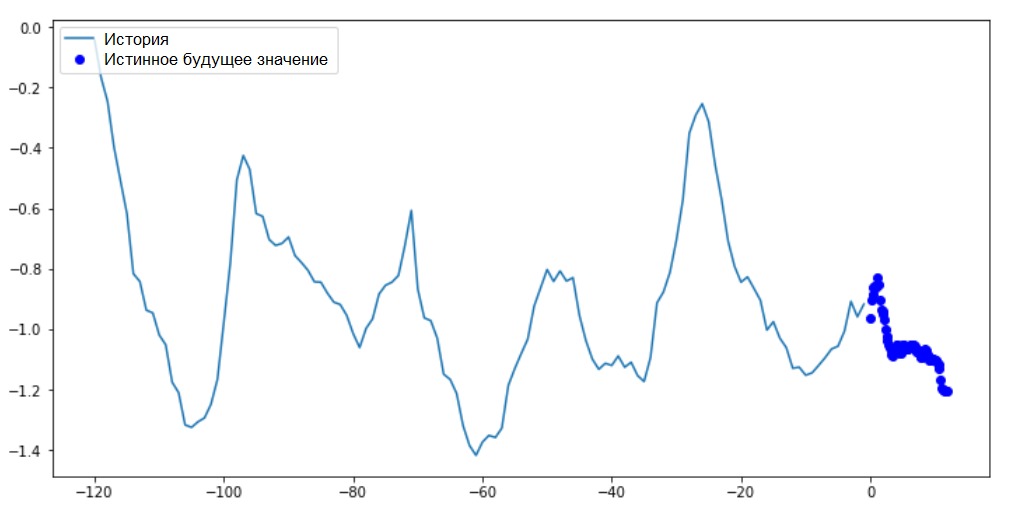 نظرًا لأن هذه المهمة أكثر تعقيدًا قليلاً من المهمة السابقة ، فإن النموذج سيتكون من طبقتين LSTM. أخيرًا ، منذ إجراء 72 التنبؤات ، تحتوي طبقة الإخراج على 72 خلية عصبية.
نظرًا لأن هذه المهمة أكثر تعقيدًا قليلاً من المهمة السابقة ، فإن النموذج سيتكون من طبقتين LSTM. أخيرًا ، منذ إجراء 72 التنبؤات ، تحتوي طبقة الإخراج على 72 خلية عصبية.multi_step_model = tf.keras.models.Sequential()
multi_step_model.add(tf.keras.layers.LSTM(32,
return_sequences=True,
input_shape=x_train_multi.shape[-2:]))
multi_step_model.add(tf.keras.layers.LSTM(16, activation='relu'))
multi_step_model.add(tf.keras.layers.Dense(72))
multi_step_model.compile(optimizer=tf.keras.optimizers.RMSprop(clipvalue=1.0), loss='mae')
سوف نتحقق من العينة ونشتق منحنيات الخسارة في مراحل التدريب والتحقق.for x, y in val_data_multi.take(1):
print (multi_step_model.predict(x).shape)
(256, 72)
multi_step_history = multi_step_model.fit(train_data_multi, epochs=EPOCHS,
steps_per_epoch=EVALUATION_INTERVAL,
validation_data=val_data_multi,
validation_steps=50)
Train for 200 steps, validate for 50 steps
Epoch 1/10
200/200 [==============================] - 21s 103ms/step - loss: 0.4952 - val_loss: 0.3008
Epoch 2/10
200/200 [==============================] - 18s 89ms/step - loss: 0.3474 - val_loss: 0.2898
Epoch 3/10
200/200 [==============================] - 18s 89ms/step - loss: 0.3325 - val_loss: 0.2541
Epoch 4/10
200/200 [==============================] - 18s 89ms/step - loss: 0.2425 - val_loss: 0.2066
Epoch 5/10
200/200 [==============================] - 18s 89ms/step - loss: 0.1963 - val_loss: 0.1995
Epoch 6/10
200/200 [==============================] - 18s 90ms/step - loss: 0.2056 - val_loss: 0.2119
Epoch 7/10
200/200 [==============================] - 18s 91ms/step - loss: 0.1978 - val_loss: 0.2079
Epoch 8/10
200/200 [==============================] - 18s 89ms/step - loss: 0.1957 - val_loss: 0.2033
Epoch 9/10
200/200 [==============================] - 18s 90ms/step - loss: 0.1977 - val_loss: 0.1860
Epoch 10/10
200/200 [==============================] - 18s 88ms/step - loss: 0.1904 - val_loss: 0.1863
plot_train_history(multi_step_history, 'Multi-Step Training and validation loss')
 إجراء تنبؤ بالفاصل الزمني، فلنكتشف مدى نجاح شبكة ANN المدربة في التعامل مع توقعات قيم درجة الحرارة المستقبلية.
إجراء تنبؤ بالفاصل الزمني، فلنكتشف مدى نجاح شبكة ANN المدربة في التعامل مع توقعات قيم درجة الحرارة المستقبلية.for x, y in val_data_multi.take(3):
multi_step_plot(x[0], y[0], multi_step_model.predict(x)[0])
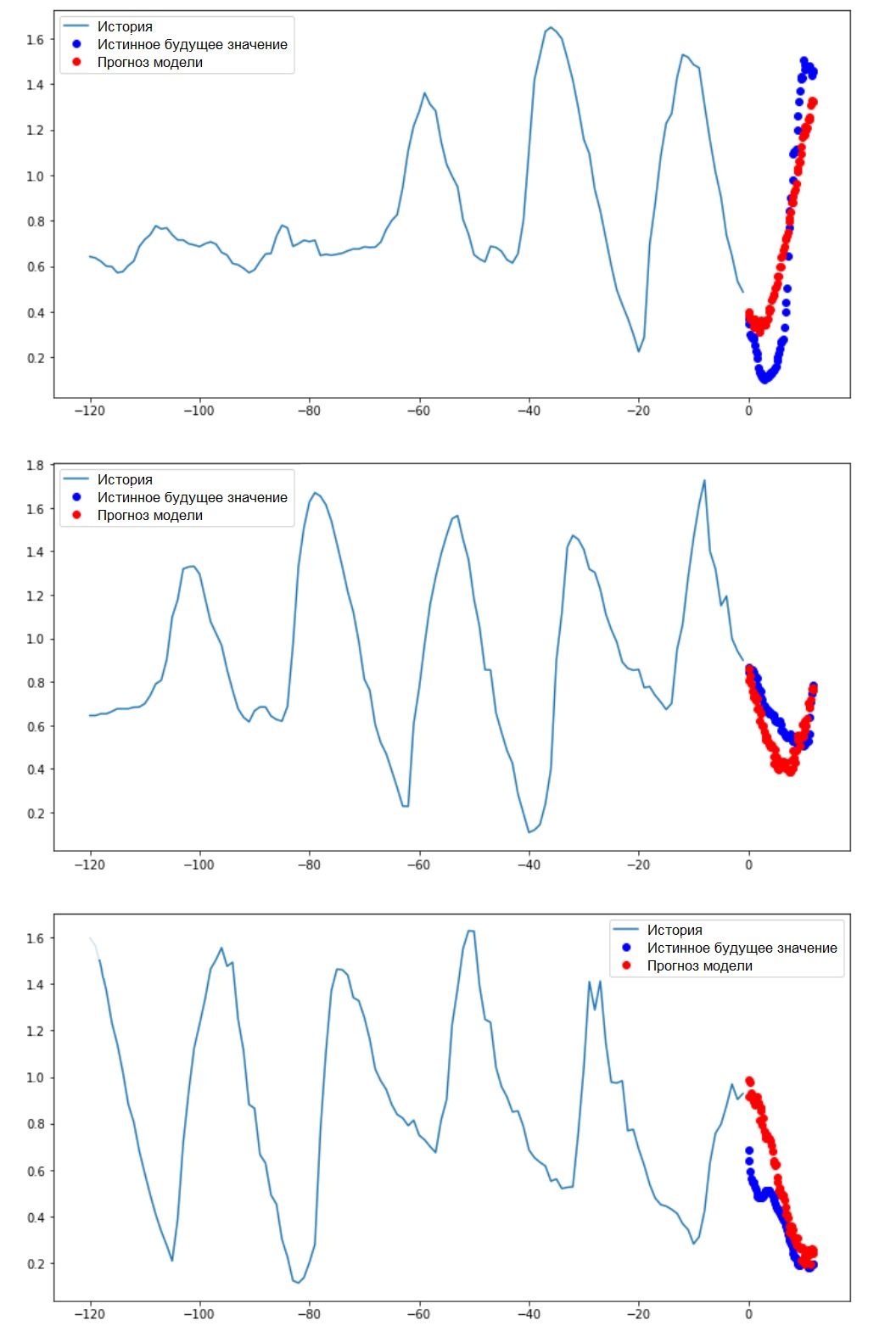
الخطوات التالية
هذا الدليل هو مقدمة موجزة لتنبؤ السلاسل الزمنية باستخدام RNS. الآن يمكنك محاولة التنبؤ بسوق الأسهم وتصبح ملياردير (في الأصل ، تمامًا مثل ذلك :). - ملحوظة مترجم) .بالإضافة إلى ذلك ، يمكنك كتابة مولدك الخاص لإعداد البيانات بدلاً من وظيفة uni / multivariate_data لاستخدام الذاكرة بشكل أكثر كفاءة. يمكنك أيضًا التعرف على عمل "إنشاء سلاسل زمنية " وتقديم أفكارها إلى هذا الدليل.لمزيد من الفهم ، يوصى بقراءة الفصل 15 من كتاب "التعلم الآلي التطبيقي باستخدام برنامج Scikit-Learn و Keras و TensorFlow" ( Aurelien Geron ، الإصدار الثاني) والفصل 6 من الكتاب"التعلم العميق في بايثون" (فرانسوا شول).الإضافة النهائية
أثناء البقاء في المنزل ، لا تهتم فقط بصحتك ، ولكن أيضًا اشفق على الكمبيوتر من خلال تنفيذ أمثلة من الدليل على مجموعة بيانات مقطوعة. على سبيل المثال ، مع مراعاة نسبة 70 × 30 (تدريب / اختبار) ، يمكنك تحديدها على النحو التالي:dataset = features[300000:].values
TRAIN_SPLIT = 85000