كودريكلاحظ مرة واحدة: "لا يوجد أبداً الكثير من مرشحات كالمان . " يمكن قول الشيء نفسه عن نظرية بايز ، لأنه من ناحية بسيط للغاية ، ولكن من ناحية أخرى يصعب فهم عمقها.

يوتيوب لديه قناة Student Dave رائعة ، ولكن تم نشر الفيديو الأخير قبل ست سنوات. تحتوي القناة على مقاطع فيديو تعليمية يروي فيها المؤلف أشياء معقدة بلغة بسيطة للغاية: نظرية بايز ، مرشح كالمان ، إلخ. الطالب ديف يكمل قصته بمثال على الحساب في matlab.

بعد أن ساعدني درس الفيديو الذي يحمل اسم "التقييم البايزي التكراري" كثيرًا (على القناة ، يتوافق مع قائمة التشغيل "التقدير البايزي التكراري: مع MATLAB") كنت أرغب في أن يتعرف الجميع على تفسيرات ديف ، ولكن للأسف لا يتم دعم المشروع. ديف نفسه لا يتصل. لا يمكنك إضافة ترجمة إلى الفيديو ، حيث يجب أن يبدأ المؤلف نفسه. لم يؤد الاتصال بـ youtube إلى نتيجة ، لذلك قررت وصف المادة في مقال باللغة الروسية ونشرها حيث يتم تقديرها للغاية. يتم تنقيح المواد واستكمالها إلى حد كبير ، لأنها مرت بتصوري الذاتي ، لذا فإن وضعها على أنها ترجمة سيكون غير مناسب. لكنني أخذت ملح التفسير نفسه من ديف. أعيدت كتابة الرمز الخاص به في python ، لأنني أعمل فيه وأعتبره بديلاً جيدًا للحزم الرياضية.

لذا ، إذا كنت تريد أن تجعل فهمًا أعمق لموضوع نظرية بايز ، مرحبًا.

صياغة المشكلة

, “ ”. .

-, . , . , . . , . . - .

إذا شاهدت الفيديو على القناة ، فستكتشف أن النينجا فشل في القفز بنجاح إلى السمان ، ولكن هذه قصة أخرى.

- $x$ . $x = 3$ . . .

( ) $N = 100$ () .

$\sigma_y^2=4$ .
, .

f_{p o s t e r i o r} (x) = \frac{f_{p r i o r} (x) \cdot f_{и з м} (x)}{\int f_{p r i o r} (x) \cdot f_{m e s} (x) d x},

$\begin{equation} f_{posterior}(x) = \frac{f_{prior}(x) \cdot f_{}(x)}{\int f_{prior}(x) \cdot f_{mes}(x) dx}, \end{equation}$

$f_{posterior}(x)$ — ;
$f_{prior}(x)$ — ;
$f_{mes}(x)$ — ( $L_x(sample)$ ).
. , ( , ):

f_{m e s} (x) = p d f (x = y, μ = x, σ = σ) = \frac{1}{2 π σ} e^{- \frac{(y - x)^{2}}{2 σ^{2}}},

$\begin{equation} f_{mes}(x) =pdf(x=y, \mu=x, \sigma=\sigma) = \frac{1}{2 \pi \sigma} e^{- \frac{(y-x)^2}{2\sigma^2}}, \end{equation}$

$pdf$ — ;
$\mu$ — ;
$\sigma$ — ;
$y$ — .
( $N$ ), , .

.
$\sigma$ , 99,7 %.

- , .

. -.
$(3, 5)$ . ( ) .

() , . .

:

f_{p o s t e r i o r} (X) = \frac{f_{p r i o r} (X) \cdot f_{и з м} (X)}{\int f_{p r i o r} (X) \cdot f_{m e s} (X) d X},

$\begin{equation} f_{posterior}(X) = \frac{f_{prior}(X) \cdot f_{}(X)}{\int f_{prior}(X) \cdot f_{mes}(X) dX}, \end{equation}$

$X$ — $\begin{pmatrix} x\\ y\end{pmatrix}$ ;
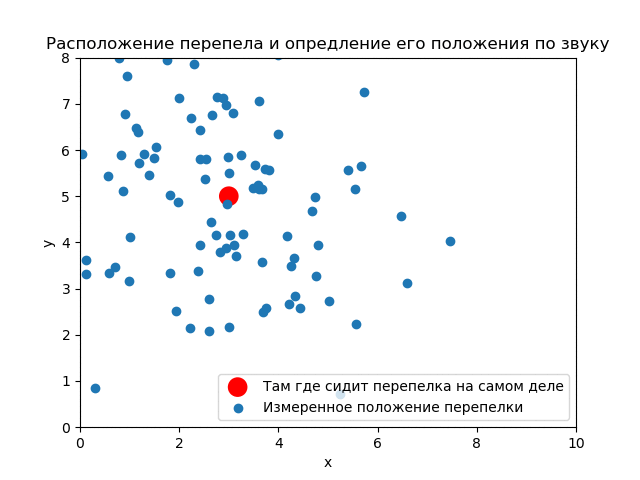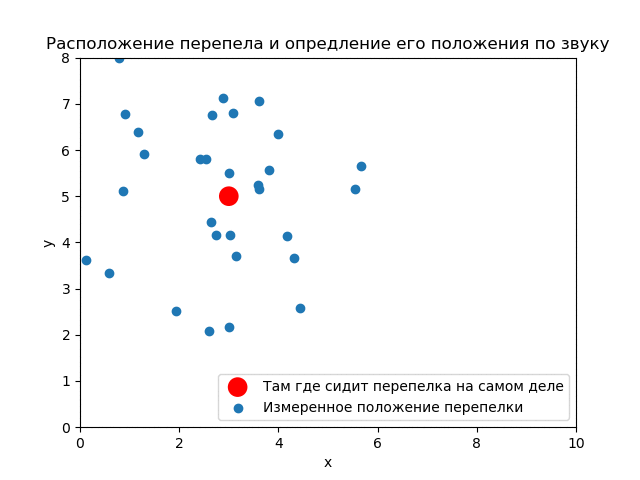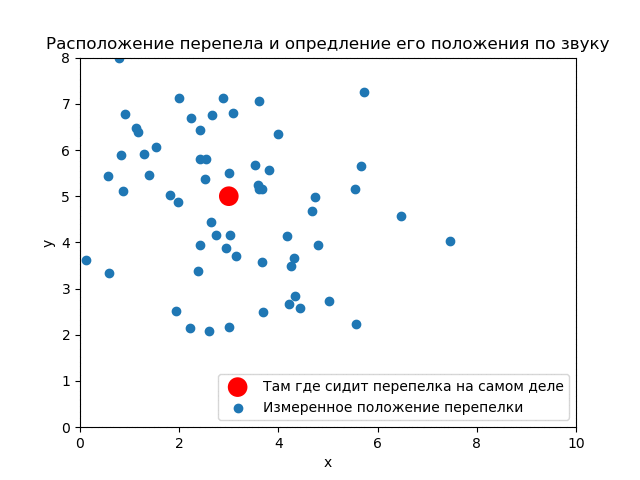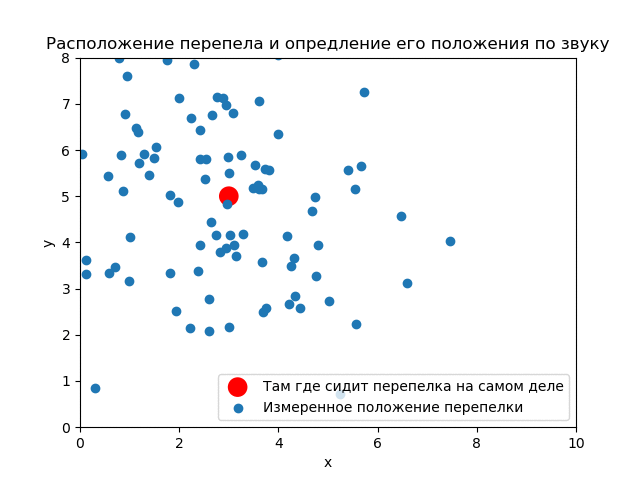
$f_{posterior}(X)$ — ;
$f_{prior}(X)$ — ;
$f_{mes}(X)$ — .
:

f_{m e s} (X) = \frac{1}{(2 π)^{2} d e t K} e^{\frac{1}{2} (Y - X)^{T} K^{- 1} (Y - X)},

$\begin{equation} f_{mes}(X) = \frac{1}{(2\pi)^2 detK} e^{ \frac {1}{2} (Y-X)^T K^{-1} (Y-X)}, \end{equation}$

$K$ — ;
$Y$ — $\begin{pmatrix} x\\ y\end{pmatrix}$ .
, .

.

, . , .
? . . , .

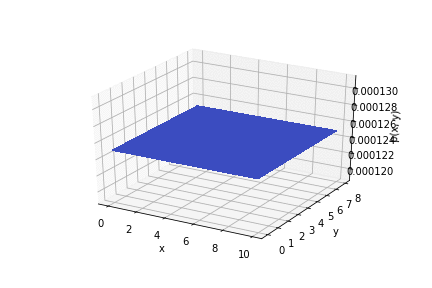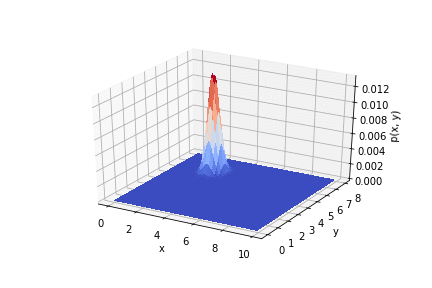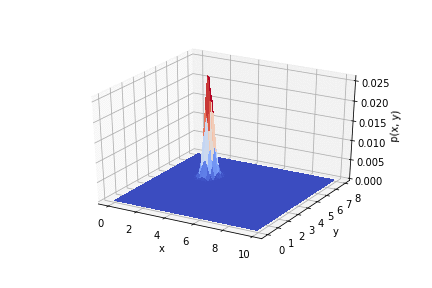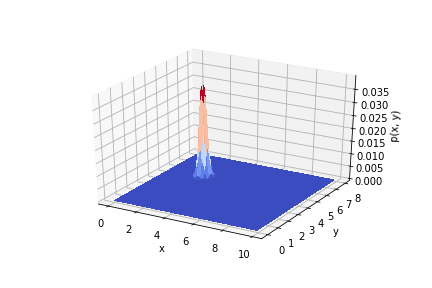
توقف عند قناة ديف خلال هذه الأسابيع من العزلة الذاتية. جيد للجميع.

Bayesian Ninja

صياغة المشكلة

More articles: