مرحبًا ، أود اليوم أن أتحدث عن تجربتي في تحليل أسهم Sberbank. في بعض الأحيان تظهر ديناميكيات مختلفة قليلاً - أصبح من المثير للاهتمام بالنسبة لي تحليل حركة اقتباساتهم.في هذا المثال ، سنقوم بتنزيل الاقتباسات من موقع Finam. رابط لتنزيل Sberbank العادي .لعمليات العمود سوف أستخدم الباندا ، لتصور matplotlib.نستورد:import pandas as pd
import matplotlib.pyplot as plt
لمنع تقلص الجداول ، يجب إزالة القيود:pd.set_option('display.max_columns', None)
pd.set_option('display.expand_frame_repr', False)
pd.set_option('max_colwidth', 80)
pd.set_option('max_rows', 6000)
قراءة بيانات المخزون
df = pd.read_csv("SBER_190101_200105.csv",sep=';', header=0, index_col='<DATE>', parse_dates=True)
(حدد الفاصل ، حيث توجد أسماء الأعمدة ، أي عمود سيكون الفهرس ، قم بتمكين تحليل التاريخ).تشير أيضًا إلى التصنيف:df = df.sort_values(by='<DATE>')
نعرض بياناتنا:print(df)
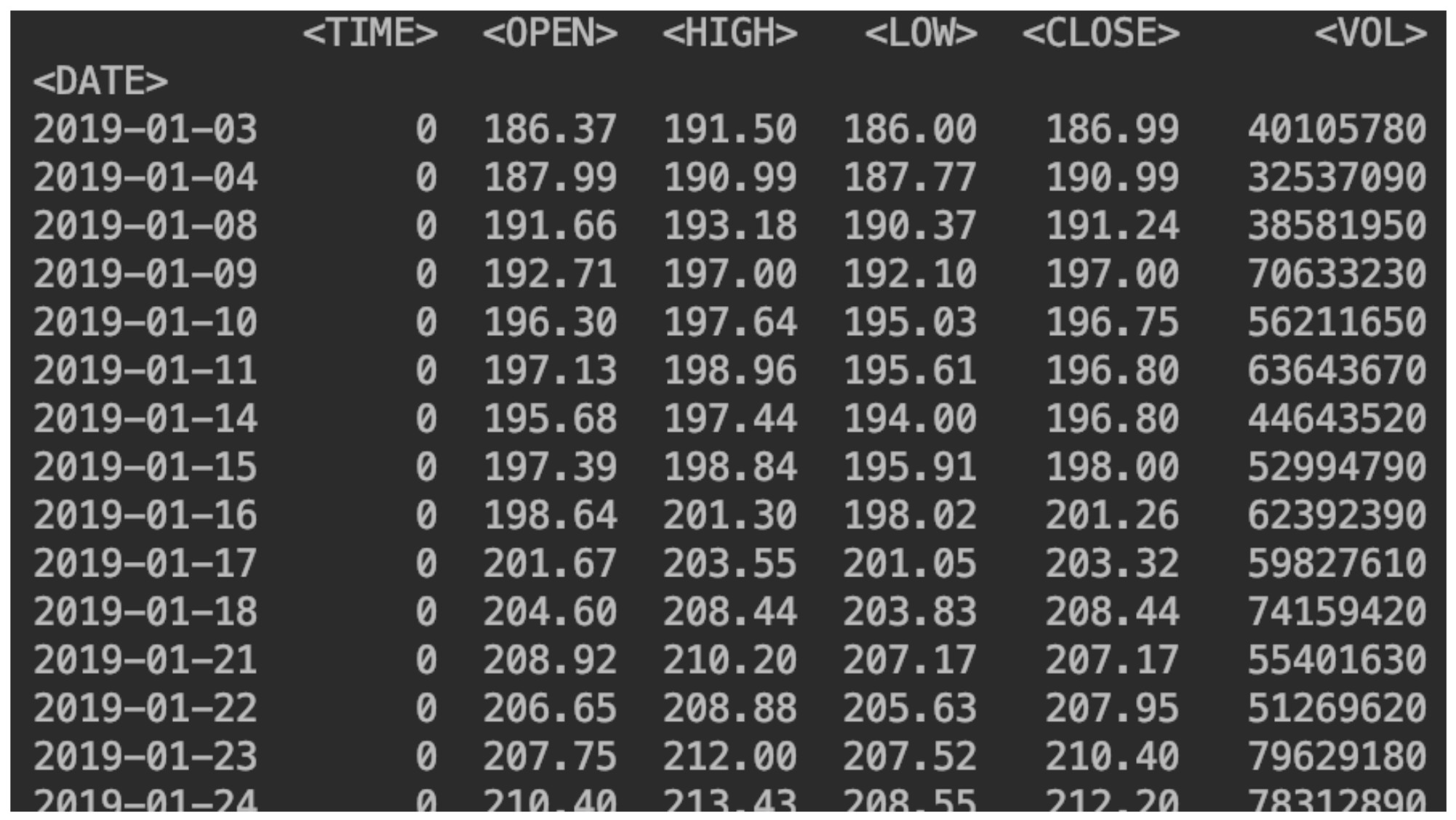 أضف عمودًا به تغيير في السعر
أضف عمودًا به تغيير في السعرdf['returns']=(df['<CLOSE>']/df['<CLOSE>'].shift(1))-1
لذا من الممكن اشتقاق النسبة بالضبط:df['returns_pers']=((df['<CLOSE>']/df['<CLOSE>'].shift(1))-1)*100

أضف حصة ثانية
افعلها بنفس الطريقة بالضبطdf2 = pd.read_csv("SBERP_190101_200105.csv",sep=';', header=0, index_col='<DATE>', parse_dates=True)
df = df.sort_values(by='<DATE>')
df2['returns_pers']=((df2['<CLOSE>']/df2['<CLOSE>'].shift(1))-1)*100
df2['returns']=(df2['<CLOSE>']/df2['<CLOSE>'].shift(1))-1
print(df2)
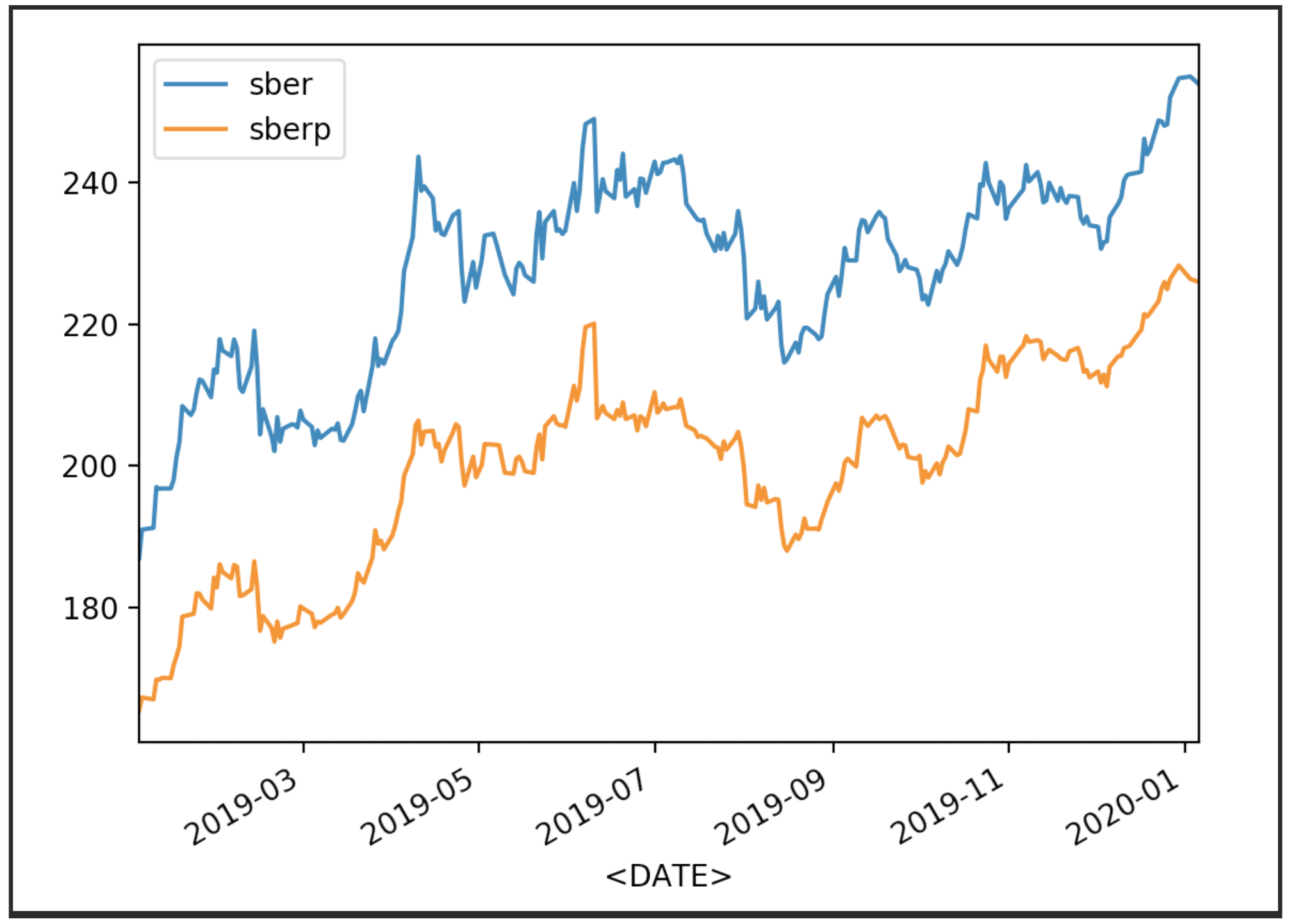
نحن نتصور أسعار الأسهم لدينا
df['<CLOSE>'].plot(label='sber')
df2['<CLOSE>'].plot(label='sberp')
plt.legend()
plt.show()
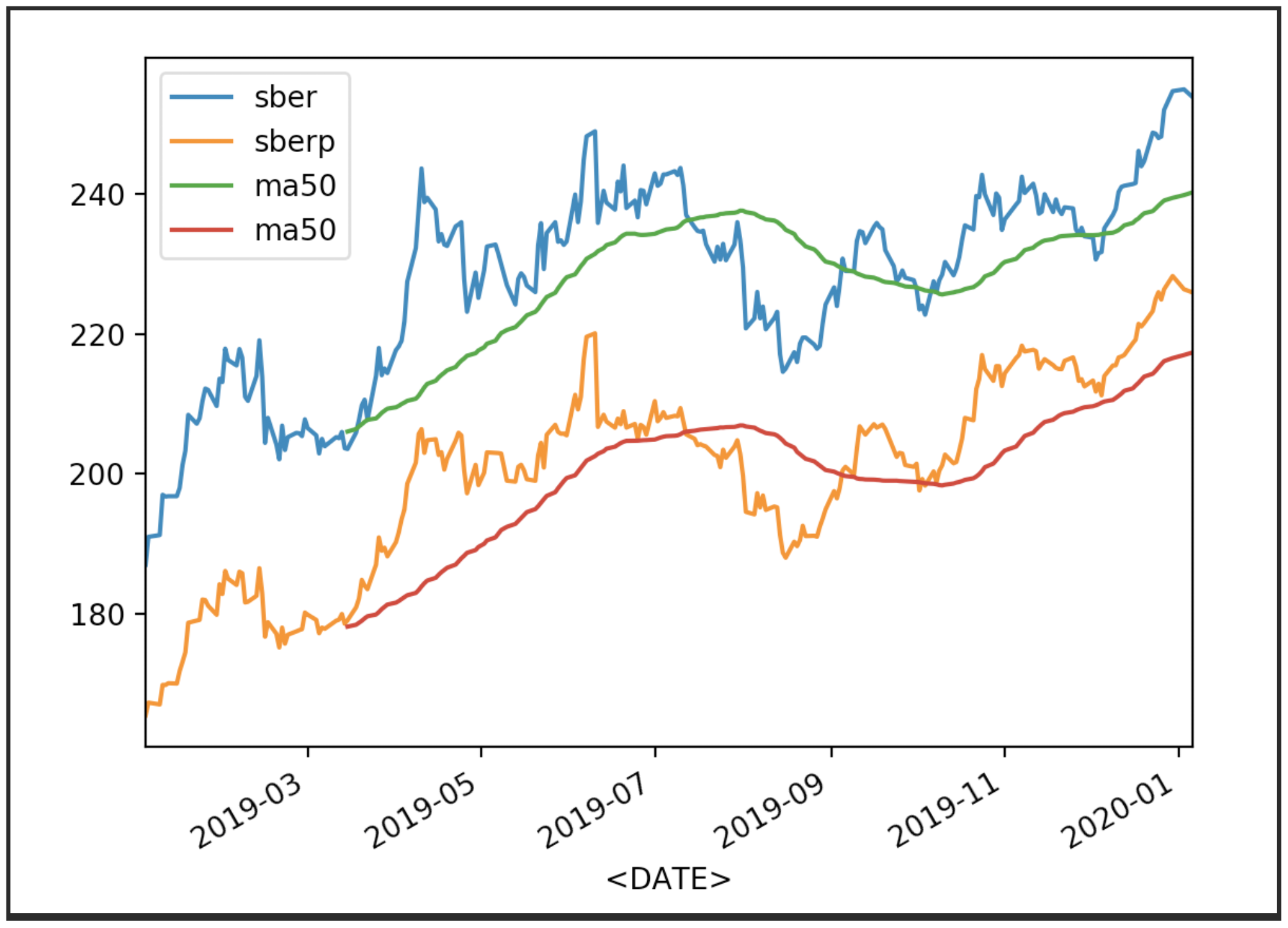
 الآن عرض الاقتباسات بمتوسطها (MA 50):
الآن عرض الاقتباسات بمتوسطها (MA 50):df['<CLOSE>'].plot(label='sber')
df2['<CLOSE>'].plot(label='sberp')
df['ma50'] = df['<OPEN>'].rolling(50).mean().plot(label='ma50')
df2['ma50'] = df2['<OPEN>'].rolling(50).mean().plot(label='ma50')
plt.legend()
plt.show()
 يمكن أيضًا عرض متوسطات أخرى.
يمكن أيضًا عرض متوسطات أخرى.df['<CLOSE>'].plot(label='sber')
df2['<CLOSE>'].plot(label='sberp')
df['ma100'] = df['<OPEN>'].rolling(100).mean().plot(label='ma100')
df2['ma100'] = df2['<OPEN>'].rolling(100).mean().plot(label='ma100')
plt.legend()
plt.show()
 سنعرض الآن حجم دوران الأسهم:أضف أيضًا اسم المحور صوحجم اللوحة
سنعرض الآن حجم دوران الأسهم:أضف أيضًا اسم المحور صوحجم اللوحةdf['total_trade'] = df['<OPEN>']*df['<VOL>']
df2['total_trade'] = df2['<OPEN>']*df2['<VOL>']
df['total_trade'].plot(label='sber',figsize=(16,8))
df2['total_trade'].plot(label='sberp',figsize=(16,8))
plt.legend()
plt.ylabel('Total Traded')
plt.show()

تحليل الارتباط
الآن دعونا نلقي نظرة فاحصة على العلاقة.سيساعدنا مخطط المصفوفة في ذلك. أنشئ جدولًا جديدًا يحتوي على أعمدة لكل من الأسهم وأعطهم أسماء.all_sber = pd.concat([df['<OPEN>'],df2['<OPEN>']],axis=1)
all_sber.columns = ['sber_open','sberp_open']
print(all_sber)
 الآن نستورد الجدول الضروري
الآن نستورد الجدول الضروريfrom pandas.plotting import scatter_matrix
وإخراجها:scatter_matrix(all_sber,figsize=(8,8),alpha=0.2,hist_kwds={'bins':100});
plt.show()
يجب أن نوضح أننا بحاجة إلى إضافة شفافية (alpha = 0.2) لرؤية تداخل النقاط.إذا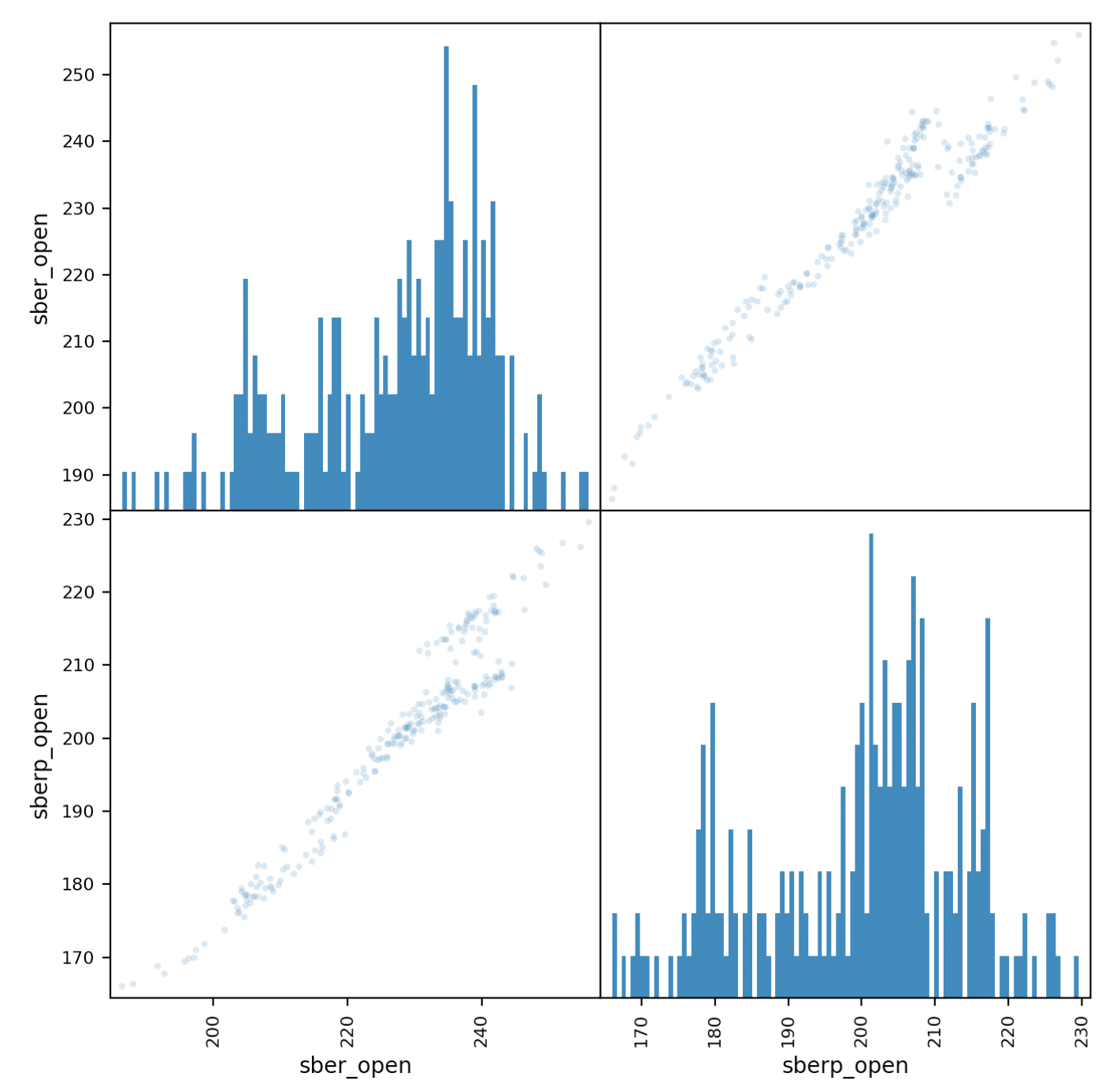 كانت "تذهب" على طول القطر ، لوحظ ارتباط.
كانت "تذهب" على طول القطر ، لوحظ ارتباط.تقييم تقلبات الأوراق المالية
df['returns_pers'].plot(label='sber')
df2['returns_pers'].plot(label='sberp')
plt.legend()
plt.show()
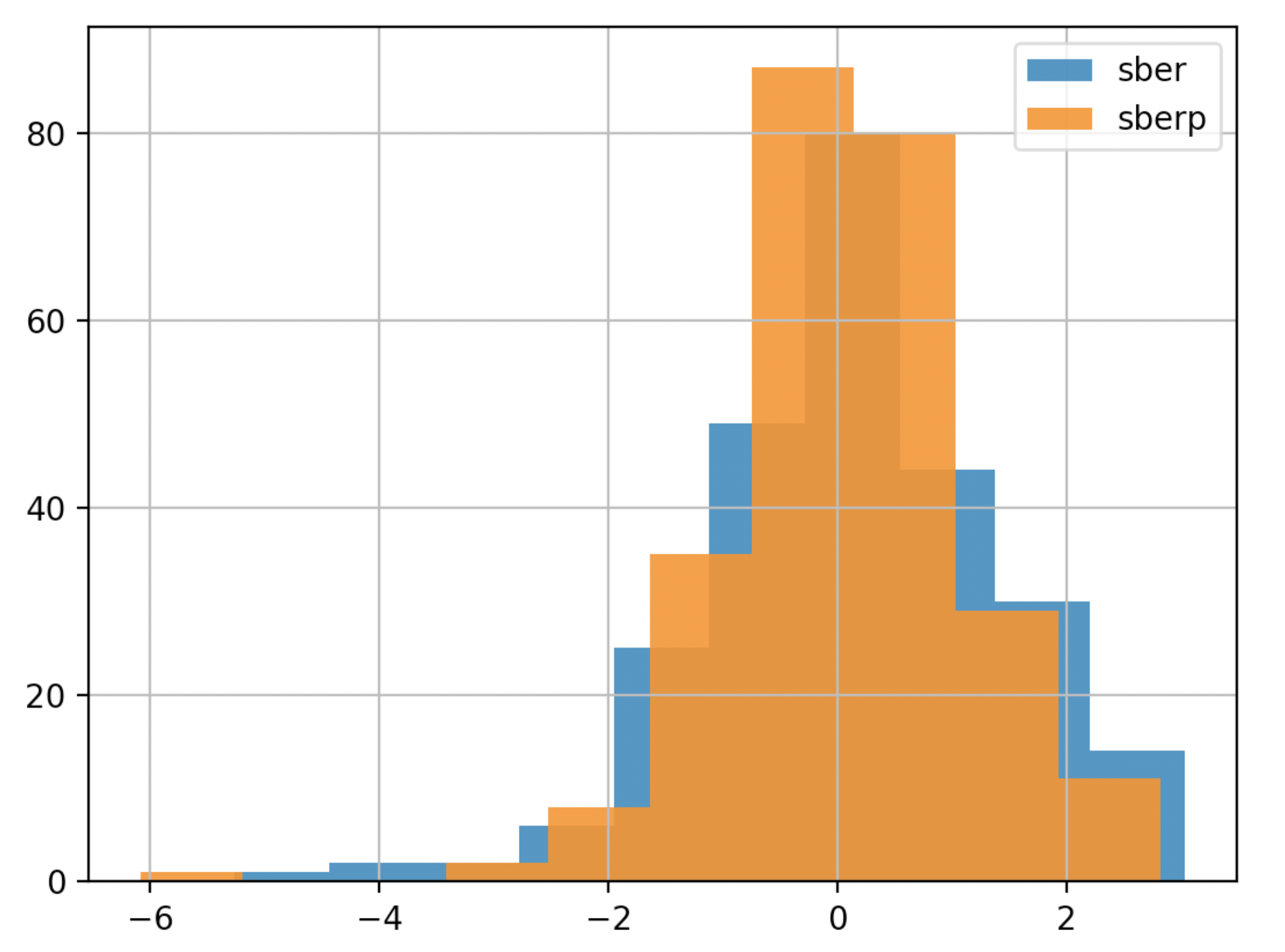
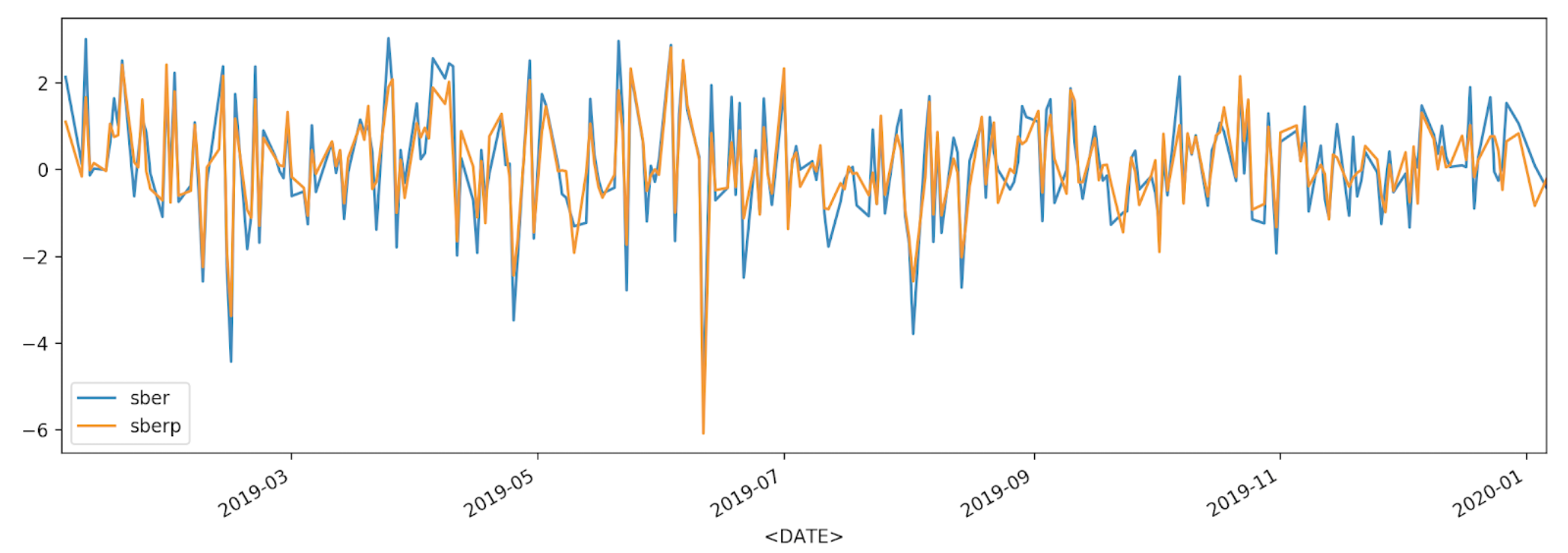 من أجل فهم أفضل ، سنعرض التقلبات على مخطط آخر - الرسم البياني
من أجل فهم أفضل ، سنعرض التقلبات على مخطط آخر - الرسم البيانيdf['returns_pers'].hist(bins=100,label='sber',alpha=0.5)
df2['returns_pers'].hist(bins=100,label='sberp',alpha=0.5)
plt.legend()
plt.show()
 لجعل الاستنتاج أسرع ، يمكنك تبسيط الجدول (سنجعل الرسم البياني أقل تفصيلاً وأقل شفافية):
لجعل الاستنتاج أسرع ، يمكنك تبسيط الجدول (سنجعل الرسم البياني أقل تفصيلاً وأقل شفافية):df['returns_pers'].hist(bins=10,label='sber',alpha=0.9)
df2['returns_pers'].hist(bins=10,label='sberp',alpha=0.9)
plt.legend()
plt.show()
تحليل الإيرادات المتراكمة
الآن إخراج النسبة المئوية للتغير في قيمة الأسهم.للقيام بذلك ، أدخل العمود مع الدخل المتراكم.df['Cumulative Return'] = (1+ df['returns']).cumprod()
df2['Cumulative Return'] = (1+ df2['returns']).cumprod()
print(df)
print(df2)
df['Cumulative Return'].plot(label='sber')
df2['Cumulative Return'].plot(label='sberp')
plt.legend()
plt.show()
 في الرسوم البيانية يمكننا أن نرى الفواصل الزمنية عندما يتم التقليل من قيمة أحد الأسهم أو إعادة تقييمه بالنسبة إلى الآخر. في الظروف الحالية (ceteris paribus ، يرجى ملاحظة) هذا سيساعدنا في اختيار سهم متوسط عند انخفاض رأس مال Sberbank.
في الرسوم البيانية يمكننا أن نرى الفواصل الزمنية عندما يتم التقليل من قيمة أحد الأسهم أو إعادة تقييمه بالنسبة إلى الآخر. في الظروف الحالية (ceteris paribus ، يرجى ملاحظة) هذا سيساعدنا في اختيار سهم متوسط عند انخفاض رأس مال Sberbank.