مرحبا يا هابر!نذكرك أننا أعلنا في وقت سابق عن كتاب " التعلم الآلي بدون كلمات إضافية " - وهو الآن معروض للبيع . على الرغم من حقيقة أنه بالنسبة للمبتدئين في MO ، يمكن أن يصبح الكتاب بالفعل سطح مكتب ، إلا أنه لم يتم لمس بعض المواضيع فيه. لذلك ، نحن نقدم لكل شخص مهتم ترجمة لمقالة كتبها Simon Kerstens حول جوهر خوارزميات MCMC مع تنفيذ مثل هذه الخوارزمية في Python.تعد طرق مونتي كارلو لسلاسل ماركوف (MCMC) فئة قوية من طرق أخذ العينات من توزيعات الاحتمالية المعروفة فقط حتى ثابت تطبيع (غير معروف) معين.ومع ذلك ، قبل الخوض في MCMC ، دعنا نناقش لماذا قد تحتاج حتى إلى إجراء مثل هذا الاختيار. الجواب: قد تكون مهتمًا إما بالعينات نفسها من العينة (على سبيل المثال ، لتحديد معلمات غير معروفة بطريقة اشتقاق بايزي) ، أو لتقريب القيم المتوقعة للوظائف المتعلقة بتوزيع الاحتمالات (على سبيل المثال ، لحساب الكميات الديناميكية الحرارية من توزيع الحالات في الفيزياء الإحصائية). في بعض الأحيان ، نحن مهتمون فقط بوضع التوزيع الاحتمالي. في هذه الحالة ، نحصل عليها بطريقة التحسين العددي ، لذلك ليس من الضروري إجراء اختيار كامل.اتضح أن أخذ العينات من أي توزيعات احتمالية باستثناء التوزيعات الأكثر بدائية هي مهمة صعبة. تعد طريقة التحويل العكسي تقنية أولية لأخذ العينات من التوزيعات الاحتمالية ، والتي تتطلب ، مع ذلك ، استخدام دالة توزيع تراكمي ، واستخدامها ، بدوره ، تحتاج إلى معرفة ثابت التطبيع ، والذي عادة ما يكون غير معروف. من حيث المبدأ ، يمكن الحصول على ثابت التطبيع من خلال التكامل العددي ، ولكن هذه الطريقة تصبح غير عملية بسرعة مع زيادة في عدد الأبعاد. أخذ عينات الانحرافلا يتطلب توزيعًا عاديًا ، ولكن من أجل تنفيذه بفعالية ، يستغرق الأمر الكثير لمعرفة توزيع الفائدة بالنسبة لنا. بالإضافة إلى ذلك ، تعاني هذه الطريقة بشدة من لعنة الأبعاد - وهذا يعني أن فعاليتها تنخفض بسرعة مع زيادة في عدد المتغيرات. هذا هو السبب في أنك تحتاج إلى تنظيم استلام العينات التمثيلية من التوزيع بذكاء - لا يتطلب معرفة ثابت التطبيع.خوارزميات MCMC هي فئة من الأساليب المصممة خصيصًا لهذا الغرض. يعودون إلى مقالة متروبوليس وغيرها . طور متروبوليس أول خوارزمية MCMC سميت باسمهومصممة لحساب حالة التوازن لنظام ثنائي الأبعاد من المجالات الصلبة. في الواقع ، كان الباحثون يبحثون عن طريقة عالمية تسمح لنا بحساب القيم المتوقعة الموجودة في الفيزياء الإحصائية.ستغطي هذه المقالة أساسيات أخذ عينات MCMC.سلاسل ماركوفالآن بعد أن فهمنا سبب حاجتنا إلى أخذ العينات ، دعنا ننتقل إلى قلب MCMC: سلاسل ماركوف. ما هي سلسلة ماركوف؟ بدون الخوض في التفاصيل التقنية ، يمكننا القول أن سلسلة ماركوف هي سلسلة عشوائية من الحالات في مساحة حالة معينة ، حيث يعتمد احتمال اختيار حالة معينة فقط على الحالة الحالية للسلسلة ، ولكن ليس على تاريخها السابق: هذه السلسلة خالية من الذاكرة. في ظل ظروف معينة ، تمتلك سلسلة ماركوف توزيعًا ثابتًا فريدًا للولايات ، تتقارب إليه ، وتتغلب على عدد معين من الحالات. بعد هذا العدد من حالات الدولة في سلسلة ماركوف ، يتم الحصول على توزيع ثابت.لأخذ عينات من التوزيع ،  تقوم خوارزمية MCMC بإنشاء ومحاكاة سلسلة ماركوف التي يكون توزيعها الثابت
تقوم خوارزمية MCMC بإنشاء ومحاكاة سلسلة ماركوف التي يكون توزيعها الثابت ؛ هذا يعني أنه بعد فترة "البذور" الأولية ، يتم توزيع حالات سلسلة ماركوف وفقًا للمبدأ
؛ هذا يعني أنه بعد فترة "البذور" الأولية ، يتم توزيع حالات سلسلة ماركوف وفقًا للمبدأ  . لذلك ، سيكون علينا فقط حفظ الحالة من أجل الحصول على عينات منها
. لذلك ، سيكون علينا فقط حفظ الحالة من أجل الحصول على عينات منها  .للأغراض التعليمية ، دعونا نفكر في كل من مساحة الدولة المنفصلة و "الوقت" المنفصل. الكمية الرئيسية التي تميز سلسلة ماركوف هي عامل انتقال
.للأغراض التعليمية ، دعونا نفكر في كل من مساحة الدولة المنفصلة و "الوقت" المنفصل. الكمية الرئيسية التي تميز سلسلة ماركوف هي عامل انتقال  يشير إلى احتمال أن تكون في حالة
يشير إلى احتمال أن تكون في حالة  في كل مرة
في كل مرة 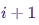 ، بشرط أن تكون السلسلة في حالة
، بشرط أن تكون السلسلة في حالة 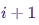 في الوقت المناسب
في الوقت المناسب i.الآن فقط للمتعة (وكمثال توضيحي) دعونا نسج بسرعة سلسلة ماركوف مع توزيع ثابت فريد. لنبدأ ببعض عمليات الاستيراد وإعدادات الرسوم البيانية:%matplotlib notebook
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10, 6]
np.random.seed(42)
سوف تدور سلسلة ماركوف حول مساحة الدولة المنفصلة التي شكلتها ثلاثة ظروف جوية:state_space = ("sunny", "cloudy", "rainy")
في فضاء حالة منفصلة ، عامل التشغيل مجرد مصفوفة. في حالتنا ، تتوافق الأعمدة والصفوف مع الطقس المشمس والغائم والممطر. دعونا نختار قيمًا معقولة نسبيًا لاحتمالات جميع التحولات:transition_matrix = np.array(((0.6, 0.3, 0.1),
(0.3, 0.4, 0.3),
(0.2, 0.3, 0.5)))
تشير الصفوف إلى الحالات التي قد توجد فيها الدائرة حاليًا ، وتشير الأعمدة إلى الحالات التي يمكن أن تنتقل إليها الدائرة. إذا اتخذنا الخطوة "المؤقتة" لسلسلة ماركوف في ساعة واحدة ، فعندئذٍ ، بشرط أن يكون الجو مشمسًا الآن ، هناك احتمال بنسبة 60٪ أن يستمر الطقس المشمس للساعة التالية. هناك أيضًا احتمال بنسبة 30٪ أن يكون الطقس غائمًا في الساعة القادمة ، واحتمال 10٪ أن تمطر فورًا بعد الطقس المشمس. هذا يعني أيضًا أن القيم في كل صف تضيف ما يصل إلى واحد.لنقود سلسلة ماركوف الخاصة بنا قليلاً:n_steps = 20000
states = [0]
for i in range(n_steps):
states.append(np.random.choice((0, 1, 2), p=transition_matrix[states[-1]]))
states = np.array(states)
يمكننا أن نلاحظ كيف تتقارب سلسلة ماركوف إلى توزيع ثابت ، مع حساب الاحتمال التجريبي لكل من الدول كدالة لطول السلسلة:def despine(ax, spines=('top', 'left', 'right')):
for spine in spines:
ax.spines[spine].set_visible(False)
fig, ax = plt.subplots()
width = 1000
offsets = range(1, n_steps, 5)
for i, label in enumerate(state_space):
ax.plot(offsets, [np.sum(states[:offset] == i) / offset
for offset in offsets], label=label)
ax.set_xlabel("number of steps")
ax.set_ylabel("likelihood")
ax.legend(frameon=False)
despine(ax, ('top', 'right'))
plt.show()
 تكريم من جميع MCMC: خوارزميات المدن الكبرىبالطبع بالطبع ، كل هذا مثير للاهتمام للغاية ، ولكن مرة أخرى إلى عملية أخذ العينات من التوزيع الاحتمالي التعسفي
تكريم من جميع MCMC: خوارزميات المدن الكبرىبالطبع بالطبع ، كل هذا مثير للاهتمام للغاية ، ولكن مرة أخرى إلى عملية أخذ العينات من التوزيع الاحتمالي التعسفي  . يمكن أن يكون إما منفصلاً ، وفي هذه الحالة سنستمر في الحديث عن مصفوفة الانتقال
. يمكن أن يكون إما منفصلاً ، وفي هذه الحالة سنستمر في الحديث عن مصفوفة الانتقال  ، أو مستمر ، وفي هذه الحالة
، أو مستمر ، وفي هذه الحالة  سيكون جوهر الانتقال. فيما يلي ، سنتحدث عن التوزيعات المستمرة ، ولكن جميع المفاهيم التي نعتبرها هنا تنطبق أيضًا على الحالات المنفصلة.إذا تمكنا من تصميم النواة الانتقالية بطريقة تم استنتاجها بالفعل من الحالة التالية
سيكون جوهر الانتقال. فيما يلي ، سنتحدث عن التوزيعات المستمرة ، ولكن جميع المفاهيم التي نعتبرها هنا تنطبق أيضًا على الحالات المنفصلة.إذا تمكنا من تصميم النواة الانتقالية بطريقة تم استنتاجها بالفعل من الحالة التالية  ، فيمكن أن يكون هذا محدودًا ، لأن سلسلة ماركوف لدينا ... ستختبر مباشرة من
، فيمكن أن يكون هذا محدودًا ، لأن سلسلة ماركوف لدينا ... ستختبر مباشرة من  . ولسوء الحظ ، لتحقيق ذلك ، نحتاج إلى القدرة على أخذ العينات منه
. ولسوء الحظ ، لتحقيق ذلك ، نحتاج إلى القدرة على أخذ العينات منه ما لا يمكننا القيام به - وإلا لن تقرأ ذلك ، أليس كذلك؟الحل هو تقسيم قلب الانتقال
ما لا يمكننا القيام به - وإلا لن تقرأ ذلك ، أليس كذلك؟الحل هو تقسيم قلب الانتقال  إلى قسمين: خطوة الاقتراح وخطوة القبول / الرفض. يظهر توزيع مساعد في خطوة العينة
إلى قسمين: خطوة الاقتراح وخطوة القبول / الرفض. يظهر توزيع مساعد في خطوة العينة يتم من خلالها تحديد الحالات التالية المحتملة للسلسلة. لا يمكننا فقط الاختيار من هذا التوزيع ، ولكن يمكننا اختيار التوزيع بشكل تعسفي. ومع ذلك ، عند التصميم ، يجب على المرء أن يسعى جاهداً للتوصل إلى تكوين تكون فيه العينات المأخوذة من هذا التوزيع مرتبطة بشكل ضئيل بالحالة الحالية وفي نفس الوقت لديها فرص جيدة للذهاب خلال مرحلة الاستلام. خطوة الاستلام / التجاوز المذكورة أعلاه هي الجزء الثاني من النواة الانتقالية ؛ في هذه المرحلة ، يتم تصحيح الأخطاء الواردة في حالات التجربة المختارة من
يتم من خلالها تحديد الحالات التالية المحتملة للسلسلة. لا يمكننا فقط الاختيار من هذا التوزيع ، ولكن يمكننا اختيار التوزيع بشكل تعسفي. ومع ذلك ، عند التصميم ، يجب على المرء أن يسعى جاهداً للتوصل إلى تكوين تكون فيه العينات المأخوذة من هذا التوزيع مرتبطة بشكل ضئيل بالحالة الحالية وفي نفس الوقت لديها فرص جيدة للذهاب خلال مرحلة الاستلام. خطوة الاستلام / التجاوز المذكورة أعلاه هي الجزء الثاني من النواة الانتقالية ؛ في هذه المرحلة ، يتم تصحيح الأخطاء الواردة في حالات التجربة المختارة من  . هنا ، يتم حساب احتمالية الاستقبال الناجح
. هنا ، يتم حساب احتمالية الاستقبال الناجح  ويتم أخذ عينة
ويتم أخذ عينة  باحتمال مثل الحالة التالية في السلسلة. الحصول على الدولة التالية
باحتمال مثل الحالة التالية في السلسلة. الحصول على الدولة التالية  من
من ثم يتم تنفيذها على النحو التالي: أولاً ،
ثم يتم تنفيذها على النحو التالي: أولاً ،  يتم أخذ حالة التجربة من
يتم أخذ حالة التجربة من  . ثم تؤخذ على أنها الحالة التالية باحتمالية
. ثم تؤخذ على أنها الحالة التالية باحتمالية  أو يتم تجاهلها باحتمال
أو يتم تجاهلها باحتمال  ، وفي الحالة الأخيرة ، يتم نسخ الحالة الحالية واستخدامها كحالة تالية.وبناء على ذلك، لدينا
، وفي الحالة الأخيرة ، يتم نسخ الحالة الحالية واستخدامها كحالة تالية.وبناء على ذلك، لدينا شرطا كافيا لسلسلة ماركوف كان
شرطا كافيا لسلسلة ماركوف كان  بمثابة توزيع ثابتة هو ما يلي: جوهر الانتقالي يجب أن يقدم التوازن مفصل أو الكتابة في الأدب البدني، الانعكاسية المجهرية :
بمثابة توزيع ثابتة هو ما يلي: جوهر الانتقالي يجب أن يقدم التوازن مفصل أو الكتابة في الأدب البدني، الانعكاسية المجهرية : .وهذا يعني أن احتمالية أن تكون في حالة
.وهذا يعني أن احتمالية أن تكون في حالة  وأن تنتقل من هناك إلى
وأن تنتقل من هناك إلى يجب أن تكون مساوية لاحتمال العملية العكسية ، أي أن تكون قادرة على
يجب أن تكون مساوية لاحتمال العملية العكسية ، أي أن تكون قادرة على  الدخول في حالة
الدخول في حالة  . تلبي نوى الانتقال لمعظم خوارزميات MCMC هذا الشرط.من أجل أن ينتقل النواة الانتقالية المكونة من جزئين إلى التوازن التفصيلي ، من الضروري الاختيار بشكل صحيح
. تلبي نوى الانتقال لمعظم خوارزميات MCMC هذا الشرط.من أجل أن ينتقل النواة الانتقالية المكونة من جزئين إلى التوازن التفصيلي ، من الضروري الاختيار بشكل صحيح  ، أي للتأكد من أنه يسمح لك بتصحيح أي اختلالات في تيار الاحتمال من / إلى
، أي للتأكد من أنه يسمح لك بتصحيح أي اختلالات في تيار الاحتمال من / إلى  أو
أو  . يستخدم حاضرة، هاستينغز خوارزمية معيار قبول متروبوليس:
. يستخدم حاضرة، هاستينغز خوارزمية معيار قبول متروبوليس: .وهنا يبدأ السحر:
.وهنا يبدأ السحر:  نحن نعرف فقط الثابت ، ولكن لا يهم ، لأن هذا الثابت غير المعروف يبطل التعبير عن
نحن نعرف فقط الثابت ، ولكن لا يهم ، لأن هذا الثابت غير المعروف يبطل التعبير عن ! إنها خاصية paccpacc هي التي تضمن تشغيل الخوارزميات بناءً على خوارزمية Metropolis-Hastings على التوزيعات غير الطبيعية. غالبًا ما يتم استخدام التوزيعات المساعدة المتماثلة ج
! إنها خاصية paccpacc هي التي تضمن تشغيل الخوارزميات بناءً على خوارزمية Metropolis-Hastings على التوزيعات غير الطبيعية. غالبًا ما يتم استخدام التوزيعات المساعدة المتماثلة ج  ، وفي هذه الحالة يتم تقليل خوارزمية متروبوليس-هاستينغز إلى خوارزمية متروبوليس الأصلية (الأقل عمومية) التي تم تطويرها في عام 1953. في الخوارزمية الأصلية
، وفي هذه الحالة يتم تقليل خوارزمية متروبوليس-هاستينغز إلى خوارزمية متروبوليس الأصلية (الأقل عمومية) التي تم تطويرها في عام 1953. في الخوارزمية الأصلية .في هذه الحالة ، يمكن كتابة النواة الانتقالية الكاملة لمتروبوليس-هاستينغز باسم
.في هذه الحالة ، يمكن كتابة النواة الانتقالية الكاملة لمتروبوليس-هاستينغز باسم .نحن ننفذ خوارزميات العواصف الحضرية في بيثونحسنًا ، الآن بعد أن اكتشفنا كيف تعمل خوارزمية Metropolis-Hastings ، دعنا ننتقل إلى تنفيذها. أولاً ، نحدد الاحتمال اللوغاريتمي للتوزيع الذي سنقوم بالاختيار منه - بدون ثوابت التطبيع ؛ من المفترض أننا لا نعرفهم. بعد ذلك ، نعمل مع التوزيع العادي القياسي:
.نحن ننفذ خوارزميات العواصف الحضرية في بيثونحسنًا ، الآن بعد أن اكتشفنا كيف تعمل خوارزمية Metropolis-Hastings ، دعنا ننتقل إلى تنفيذها. أولاً ، نحدد الاحتمال اللوغاريتمي للتوزيع الذي سنقوم بالاختيار منه - بدون ثوابت التطبيع ؛ من المفترض أننا لا نعرفهم. بعد ذلك ، نعمل مع التوزيع العادي القياسي:def log_prob(x):
return -0.5 * np.sum(x ** 2)
بعد ذلك ، نختار توزيعًا مساعدًا متماثلًا. بشكل عام ، يمكن تحسين أداء خوارزمية Metropolis-Hastings إذا قمت بتضمين معلومات معروفة لك بالفعل عن التوزيع الذي ترغب في تحديد منه في التوزيع الإضافي. يبدو النهج المبسط كما يلي: نأخذ الحالة الحالية xونختار عينة من  ، أي تعيين حجم خطوة معين
، أي تعيين حجم خطوة معين Δوننتقل يسارًا أو يمينًا من حالتنا الحالية بما لا يزيد عن  :
:def proposal(x, stepsize):
return np.random.uniform(low=x - 0.5 * stepsize,
high=x + 0.5 * stepsize,
size=x.shape)
أخيرًا ، نحسب احتمالية قبول الاقتراح:def p_acc_MH(x_new, x_old, log_prob):
return min(1, np.exp(log_prob(x_new) - log_prob(x_old)))
الآن نضع كل هذا معًا في تنفيذ موجز حقًا لمرحلة أخذ العينات لخوارزمية Metropolis-Hastings:def sample_MH(x_old, log_prob, stepsize):
x_new = proposal(x_old, stepsize)
accept = np.random.random() < p_acc(x_new, x_old, log_prob)
if accept:
return accept, x_new
else:
return accept, x_old
بالإضافة إلى الحالة التالية في سلسلة ماركوف ، x_newأو x_oldنعيد أيضًا معلومات حول ما إذا تم اعتماد خطوة MCMC. سيسمح لنا هذا بتتبع ديناميكيات جمع العينات. في ختام هذا التنفيذ ، نكتب وظيفة ستستدعي تكرارًا sample_MHوبناء سلسلة ماركوف:def build_MH_chain(init, stepsize, n_total, log_prob):
n_accepted = 0
chain = [init]
for _ in range(n_total):
accept, state = sample_MH(chain[-1], log_prob, stepsize)
chain.append(state)
n_accepted += accept
acceptance_rate = n_accepted / float(n_total)
return chain, acceptance_rate
اختبار خوارزمياتنا في المترو متروبوليس والبحث عن سلوكهاربما ، الآن لا يمكنك الانتظار لرؤية كل هذا في العمل. سنفعل ذلك ، وسنتخذ بعض القرارات المستنيرة حول الحجج stepsizeو n_total:chain, acceptance_rate = build_MH_chain(np.array([2.0]), 3.0, 10000, log_prob)
chain = [state for state, in chain]
print("Acceptance rate: {:.3f}".format(acceptance_rate))
last_states = ", ".join("{:.5f}".format(state)
for state in chain[-10:])
print("Last ten states of chain: " + last_states)
Acceptance rate: 0.722
Last ten states of chain: -0.84962, -0.84962, -0.84962, -0.08692, 0.92728, -0.46215, 0.08655, -0.33841, -0.33841, -0.33841
الأمور جيدة. لذا ، هل نجحت؟ نجحنا في أخذ عينات في حوالي 71٪ من الحالات ، ولدينا سلسلة من الحالات. يجب تجاهل الحالات القليلة الأولى التي لم تتقارب فيها السلسلة بعد إلى توزيعها الثابت. دعنا نتحقق مما إذا كانت الشروط التي اخترناها تحتوي بالفعل على توزيع طبيعي:def plot_samples(chain, log_prob, ax, orientation='vertical', normalize=True,
xlims=(-5, 5), legend=True):
from scipy.integrate import quad
ax.hist(chain, bins=50, density=True, label="MCMC samples",
orientation=orientation)
if normalize:
Z, _ = quad(lambda x: np.exp(log_prob(x)), -np.inf, np.inf)
else:
Z = 1.0
xses = np.linspace(xlims[0], xlims[1], 1000)
yses = [np.exp(log_prob(x)) / Z for x in xses]
if orientation == 'horizontal':
(yses, xses) = (xses, yses)
ax.plot(xses, yses, label="true distribution")
if legend:
ax.legend(frameon=False)
fig, ax = plt.subplots()
plot_samples(chain[500:], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()
 تبدو جيدة!ماذا عن المعلمات
تبدو جيدة!ماذا عن المعلمات stepsizeو n_total؟ نناقش أولاً حجم الخطوة: فهو يحدد إلى أي مدى يمكن إزالة حالة التجربة من الحالة الحالية للدائرة. لذلك ، هذه معلمة توزيع مساعدة qتتحكم في حجم الخطوات العشوائية التي تتخذها سلسلة ماركوف. إذا كان حجم الخطوة كبيرًا جدًا ، فغالبًا ما تنتهي حالات التجربة في ذيل التوزيع ، حيث تكون قيم الاحتمال منخفضة. تتجاهل آلية أخذ العينات متروبوليس-هاستينغز معظم هذه الخطوات ، ونتيجة لذلك يتم تخفيض معدلات الاستقبال ويتباطأ التقارب بشكل ملحوظ. انظر بنفسك:def sample_and_display(init_state, stepsize, n_total, n_burnin, log_prob):
chain, acceptance_rate = build_MH_chain(init_state, stepsize, n_total, log_prob)
print("Acceptance rate: {:.3f}".format(acceptance_rate))
fig, ax = plt.subplots()
plot_samples([state for state, in chain[n_burnin:]], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()
sample_and_display(np.array([2.0]), 30, 10000, 500, log_prob)
Acceptance rate: 0.116
 ليس رائعًا ، أليس كذلك؟ الآن يبدو أنه من الأفضل تعيين حجم خطوة صغير. اتضح أن هذا ليس قرارًا ذكيًا أيضًا ، لأن سلسلة ماركوف ستحقق في التوزيع الاحتمالي ببطء شديد ، وبالتالي لن تتقارب بالسرعة نفسها كما هو الحال مع حجم الخطوة المختار جيدًا:
ليس رائعًا ، أليس كذلك؟ الآن يبدو أنه من الأفضل تعيين حجم خطوة صغير. اتضح أن هذا ليس قرارًا ذكيًا أيضًا ، لأن سلسلة ماركوف ستحقق في التوزيع الاحتمالي ببطء شديد ، وبالتالي لن تتقارب بالسرعة نفسها كما هو الحال مع حجم الخطوة المختار جيدًا:sample_and_display(np.array([2.0]), 0.1, 10000, 500, log_prob)
Acceptance rate: 0.992
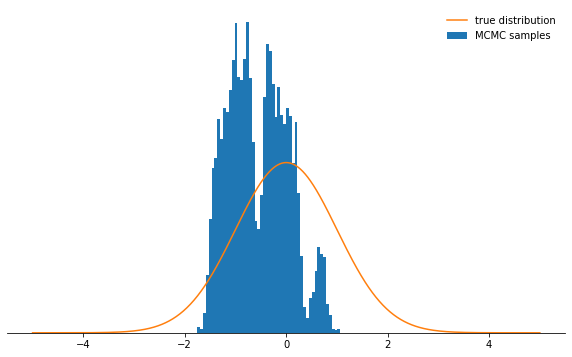 بغض النظر عن كيفية اختيار معلمة حجم الخطوة ، تتحول سلسلة ماركوف في النهاية إلى توزيع ثابت. لكن هذا قد يستغرق الكثير من الوقت. يتم تحديد الوقت الذي سنقوم فيه بمحاكاة سلسلة ماركوف بواسطة المعلمة
بغض النظر عن كيفية اختيار معلمة حجم الخطوة ، تتحول سلسلة ماركوف في النهاية إلى توزيع ثابت. لكن هذا قد يستغرق الكثير من الوقت. يتم تحديد الوقت الذي سنقوم فيه بمحاكاة سلسلة ماركوف بواسطة المعلمة n_total- فهو ببساطة يحدد عدد حالات سلسلة ماركوف (وبالتالي العينات المحددة) التي سنحصل عليها في النهاية. إذا كانت السلسلة تتقارب ببطء ، فيجب زيادتها n_totalبحيث يكون لدى سلسلة ماركوف الوقت "لننسى" الحالة الأولية. لذلك ، سنترك حجم الخطوة صغيرًا ونزيد عدد العينات عن طريق زيادة المعلمة n_total:sample_and_display(np.array([2.0]), 0.1, 500000, 25000, log_prob)
Acceptance rate: 0.990
 Meeeedenly نحن نتحرك نحو الهدف ...الاستنتاجاتبالنظر إلى كل ما سبق ، آمل أن تكون قد فهمت الآن حدسيًا خوارزمية متروبوليس-هاستينغز ، ومعلماتها ، وفهم لماذا هذه أداة مفيدة للغاية للاختيار من توزيعات الاحتمالية غير القياسية التي قد تواجهها في الممارسة.أوصي بشدة بتجربة الشفرة الواردة هنا.- حتى تعتاد على سلوك الخوارزمية في مختلف الظروف وتفهمها بشكل أعمق. جرب التوزيع المساعد غير المتماثل! ماذا سيحدث إذا لم تقم بتكوين معيار القبول بشكل صحيح؟ ماذا يحدث إذا حاولت أخذ عينة من التوزيع الثنائي؟ هل يمكنك التوصل إلى طريقة لضبط حجم الخطوة تلقائيًا؟ ما هي المزالق هنا؟ أجب على هذه الأسئلة بنفسك!
Meeeedenly نحن نتحرك نحو الهدف ...الاستنتاجاتبالنظر إلى كل ما سبق ، آمل أن تكون قد فهمت الآن حدسيًا خوارزمية متروبوليس-هاستينغز ، ومعلماتها ، وفهم لماذا هذه أداة مفيدة للغاية للاختيار من توزيعات الاحتمالية غير القياسية التي قد تواجهها في الممارسة.أوصي بشدة بتجربة الشفرة الواردة هنا.- حتى تعتاد على سلوك الخوارزمية في مختلف الظروف وتفهمها بشكل أعمق. جرب التوزيع المساعد غير المتماثل! ماذا سيحدث إذا لم تقم بتكوين معيار القبول بشكل صحيح؟ ماذا يحدث إذا حاولت أخذ عينة من التوزيع الثنائي؟ هل يمكنك التوصل إلى طريقة لضبط حجم الخطوة تلقائيًا؟ ما هي المزالق هنا؟ أجب على هذه الأسئلة بنفسك!