بدأت الرغبة المفرطة في الدقة لها تأثير يبطل نظرية التحكم ونظرية النظم ، لأنها تؤدي إلى حقيقة أن البحث في هذا المجال يركز على تلك المشاكل فقط والتي يمكن حلها بدقة. العديد من فئات المشاكل المهمة التي تكون فيها البيانات والأهداف والقيود معقدة للغاية أو غير محددة بشكل جيد للسماح بالتحليل الرياضي الدقيق ، وقد بقيت على الهامش فقط لأنه لا يمكن تفسيرها رياضيًا. زادي
التعريف والخصائص
في العالم ، لا ينقسم الكثير فقط إلى الأبيض والأسود ، إلى الحقيقة والحقيقة ... يستخدم الشخص العديد من المفاهيم الغامضة لتقييم ومقارنة الكميات المادية ، وحالات الأشياء والأنظمة على المستوى النوعي التقريبي. لذا ، فإن أيًا منا قادر على تقدير درجة الحرارة خارج النافذة ، دون اللجوء إلى مقياس الحرارة ، ولا يسترشد إلا بمشاعرنا الخاصة ومقياس التقديرات التقريبية ("ملبد بالغيوم بما يكفي لأخذ مظلة").
لكن التقييم النوعي لا يمتلك خاصية الإضافة المتأصلة في أعدادنا المعتادة ؛ أي أنه لا يمكننا تحديد نتيجة العمليات لتقديرات تقريبية ("مبلغ صغير من المال" + "مبلغ صغير من المال") ، على النقيض من ، على سبيل المثال ، الأرقام الطبيعية (2 + 2). لا يمكننا التحديد لأن التقييم النوعي يعتمد بشدة على صانع القرار والسياق والمعنى المستثمر في حالة معينة.
ومع ذلك ، في العالم هناك كميات كافية لا يمكننا تقييمها بدقة لسبب أو لآخر: درجة النظام في الغرفة ، "هيبة" السيارة ، جمال الشخص ، "تشابه" الأشياء ... لكني أريد العمل معهم كما هو الحال مع الأرقام المعتادة على الرغم من سيكون لمهام الأتمتة.
يمكن أن يعتمد إضفاء الطابع الرسمي على هذه التقديرات على نظرية المجموعات الضبابية. ظهر مفهوم المجموعات الضبابية في عام 1964 بفضل عالم أمريكي من أصل أذربيجاني لطفي زاده .
نبدأ النظر في نظريته مع المفاهيم الأساسية.
مجموعة ضبابية ( غامض مجموعة)  في المجموعة العالمية (الكون) U هي مجموعة من الأزواج
في المجموعة العالمية (الكون) U هي مجموعة من الأزواج )%20) ، حيث
، حيث  و
و
%20) - وظيفة عضوية مجموعة غامض
- وظيفة عضوية مجموعة غامض  ،
، ![\ mu_A (u): U → [0؛ 1]](https://tex.s2cms.ru/svg/%20%5Cmu_A%20(u)%3AU%20%E2%86%92%5B0%3B1%5D%20) . يمكن أيضًا كتابة مجموعات غامضة كـ
. يمكن أيضًا كتابة مجموعات غامضة كـ %7D(%5Cmu_A%20(u)%20%2F%20u)%20%3D%20%5Cleft%5C%7B%20%20(%5Cmu_A(u)%20%2F%20u)%20%5Cright%5C%7D%20%20) .
.
U %20) ( ) u (-)
( ) u (-)  . , . - .
. , . - .
%20) ( . ), – . – U
( . ), – . – U  . , , .
. , , .
, %20%3D%20%5Cbegin%7Bcases%7D1%20%26%20u%20%5Csubseteq%20A%20%5C%5C0%20%26%20u%20%5Cnsubseteq%20A%20%5Cend%7Bcases%7D%20) , .
, .
, %20) :
:
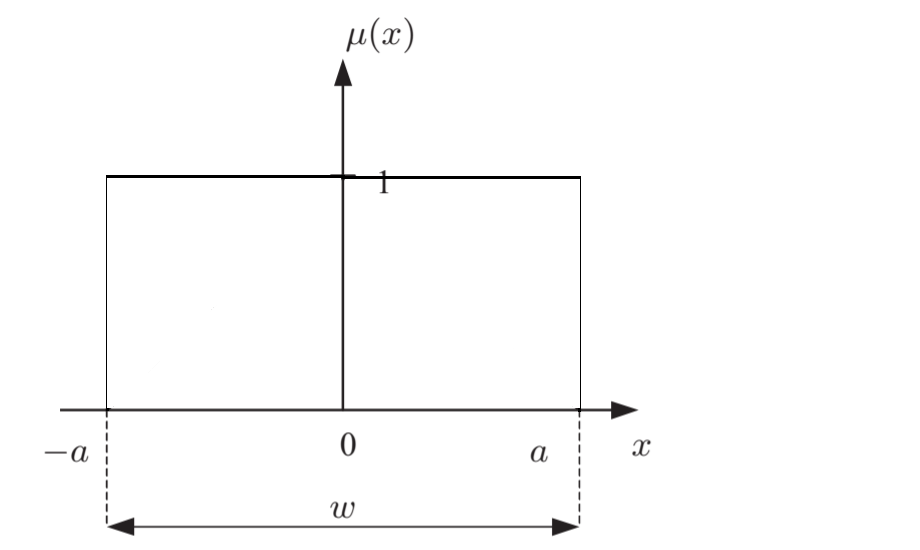
-a≤x≤a.
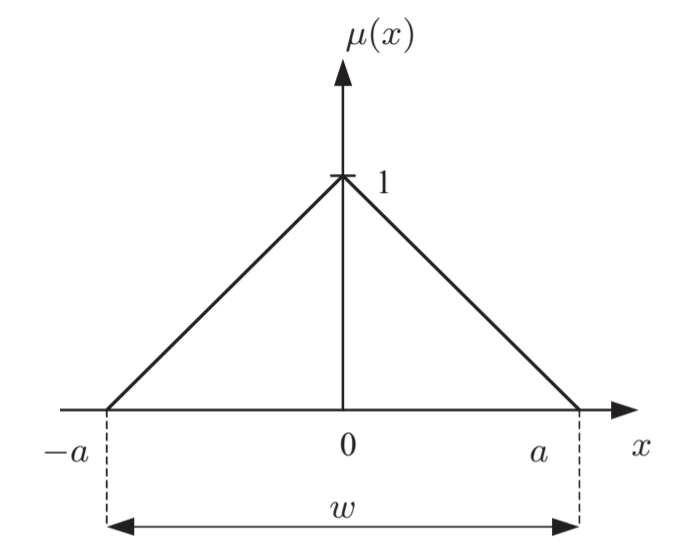
“ ”.
%3D%20%5Cfrac%7B(a-%7Cx%7C)%7D%7Ba%7D%2C%20%20-a%20%5Cleq%20x%20%5Cleq%20a%20)
 .
.
.
– , 1. 0.
, %20) 0.5, . -a/2 a/2.
0.5, . -a/2 a/2.
)%2Cu%20%5Csubseteq%20U%20) .
.
, 1, . – .
, , 0, .
, 1 .
2 %20)
%3E0%2C%20%20x%20%5Csubseteq%20X%20%5Cright%5C%7D%20) –
–  .
. 
 .
.
, x, %3D0%20) ; –
; – %7D%3D0%20) .
.
, , . :
- , ;
- , ;
- , , .
:  — U,
— U,  . , .
. , .
 ,
, %3D%20%5Cmu_B(x)%20) .
.
 ,
, %20%5Cleq%20%0A%20%5Cmu_B%20(x)%20) x.
x.
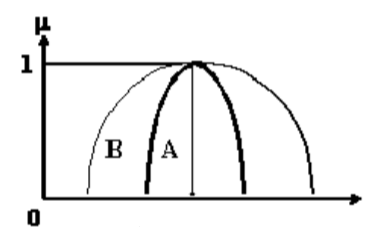
 ,
, %20%3D%20max%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20) . ,
. , %20%3D%20%5Cmu_A(x)%20%5Cvee%20%5Cmu_B%20(x)%20) . (t– s–)
. (t– s–)
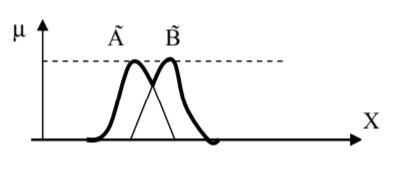
 ,
, %20%3D%20min%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20) . ,
. , %20%3D%20%5Cmu_A(x)%20%5Cwedge%20%5Cmu_B%20(x)%20) . (t-)
. (t-)
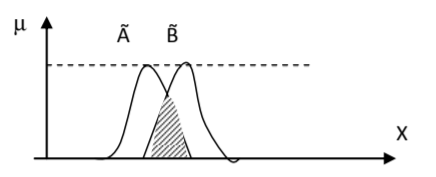
:
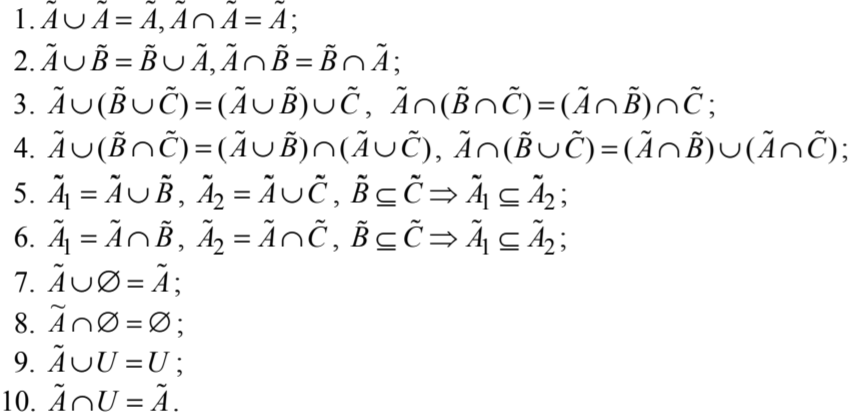
. , , . , min max .
 ,
, %20%3D%20%5Cmu_A(x)%20-%20%5Cmu_%7BA%20%5Ccap%20B%7D(x)%20%3D%20%5Cmu_A(x)%20-%20min%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20%3D%20max(0%3B%20%5Cmu_A(x)%20-%20%5Cmu_B(x))%20) .
.

 . ,
. , %20%3D%201-%20%5Cmu_%7B%5Coverline%7BA%7D%7D(x)%20) .
.
. , , , (,  ). :
). :
α- . α-  ,
, %20%5Cgeq%20%5Calpha%20) .
.
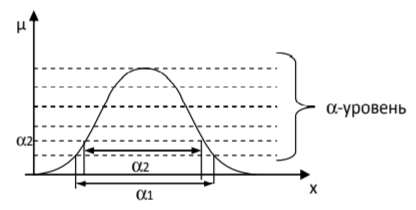
.  , M — .
, M — .
 ,
, %3D%20%5Cmu_A%5E%7B%5Cbeta%7D(x)%20) . :
. :
- β = 2 ( CON(A) ). , . , “ ” ;
- β = 0.5 ( DIL(A) ). , . “ ”.
.
%20%3D%20%5Cmu_A(x)%20*%20%5Cmu_B%20(x)%20) .
.
%20%3D%20(%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%201)%20%5Cvee%200%20) .
.
%20%3D%20%5Cbegin%7Bcases%7D%5Cmu_B(x)%20%26%20%5Cmu_A(x)%20%3D%201%5C%5C%5Cmu_A(x)%20%26%20%5Cmu_B(x)%20%3D%201%5C%5C0%20%26%20%5Cend%7Bcases%7D%20) .
.
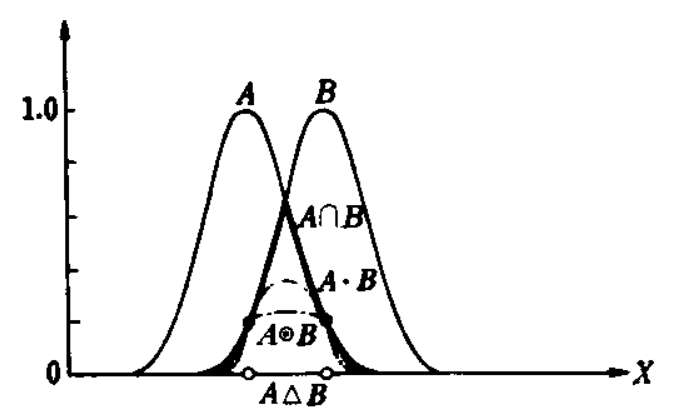
%20%3D%20%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%20%5Cmu_A(x)*%5Cmu_B(x)) .
.
%20%3D%20(%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%201)%20%5Cwedge%201%20) .
.
%20%3D%20%5Cbegin%7Bcases%7D%5Cmu_B(x)%20%26%20%5Cmu_A(x)%20%3D%200%5C%5C%5Cmu_A(x)%20%26%20%5Cmu_B(x)%20%3D%200%5C%5C1%20%26%20%5Cend%7Bcases%7D%20) .
.
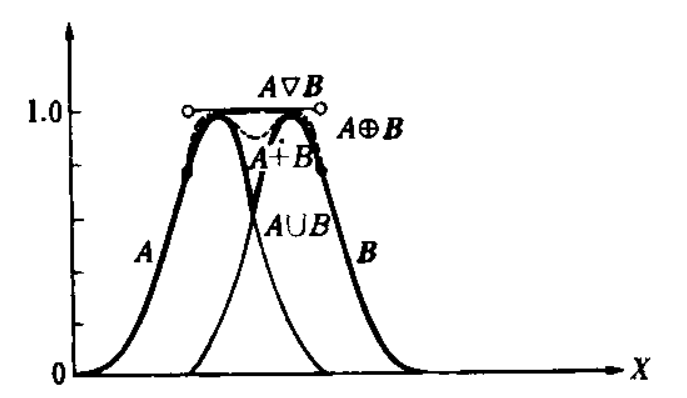
- – A B λ (1 — λ) ( A B). %20%3D%20%5Clambda%20*%20%5Cmu_A(x)%20%2B%20(1%20-%20%5Clambda)%20*%20%5Cmu_B(x)%20) .
.
, λ- :

?
, , . . , ( , ). 2 – .
, . , , , . : , .
, , . , .
, , , , , :
- 0 <= μ(x) <= 1;
- ( );
- يجب أن تحتوي الوظيفة ومجموعة الوظائف المحددة على تمييز طبيعي للمفاهيم التي تمثلها المجموعات المجاورة ؛
- يجب ألا تكون هناك فجوات في مجموعة عالمية (أو محدودة للنظر) لا ترتبط بها مجموعة ؛
- بالنسبة للمجموعات المجاورة ، يجب أن يتطابق الحد الأقصى لأحدهما مع الحد الأدنى للآخر ، ويجب أن تتوافق نقطة تقاطع الرسوم البيانية الخاصة بهم مع نقاط الانتقال ؛
- وبعض المهام الأخرى الخاصة بالمهمة.
على الرغم من وجود حالات استثنائية يجب فيها تحديد الوظيفة بناءً على السياق. بناء مثل هذه الوظائف هو موضوع منفصل ومعقد إلى حد ما.
وهذا كل شيء لهذا اليوم.