تجارة المراجحة (خوارزمية Bellman-Ford)

عادة ما يرتبط التداول في البورصة بالمخاطر. هذا صحيح تمامًا لمعظم استراتيجيات التداول. يتم تحديد نجاح التجارة في هذه الحالات فقط من خلال القدرة على تقييم المخاطر بشكل صحيح وإدارتها. ولكن ليست كل استراتيجيات التداول. هناك استراتيجيات خالية من المخاطر ، والتي تشمل ، على وجه الخصوص ، التحكيم. تشرح هذه المقالة ماهية التحكيم وكيفية تنفيذه باستخدام خوارزمية الرسم البياني الكلاسيكية مثل خوارزمية بلمان-فورد.

ما هو التحكيم؟

التحكيم هو عدد قليل من المعاملات ذات الصلة المنطقية التي تهدف إلى الربح من الفرق في أسعار نفس الأصول أو الأصول ذات الصلة في نفس الوقت في أسواق مختلفة (التحكيم المكاني) ، أو في نفس السوق في نقاط زمنية مختلفة (التحكيم المؤقت) .

كمثال بسيط ، خذ بعين الاعتبار المراجحة المكانية. في نيويورك ولندن ، يمكن إبرام صفقات لشراء الدولار مقابل اليورو واليورو مقابل الدولار. في نيويورك ، يمكن القيام بذلك بمعدل 4 دولارات مقابل 3 يورو ، وفي لندن - بمعدل 5 دولارات مقابل 3 يورو. يفتح هذا الاختلاف في المعدلات إمكانية التحكيم المكاني.



مع 4 دولارات ، يمكنك شراء 3 يورو في نيويورك. بعد ذلك ، في لندن ، قم بشراء هذه 3 يورو 5 دولارات. كما ترون ، فإن هذا التسلسل البسيط للمعاملات يجلب ربحًا واحدًا للدولار لكل 4 دولارات يتم استثمارها. وفقا لذلك ، إذا كان هناك في البداية 4 ملايين دولار ، فإن الربح سيكون بالفعل في مليون.

عندما تختلف أسعار الصرف (لا نعتبر السبريد) لنفس زوج العملات ، فإن تسلسل المعاملات المطلوبة لتنفيذ استراتيجية المراجحة يكون بسيطًا للغاية. إذا كان سعر الصرف لزوج عملات واحد ثابتًا ، ولكن يتم تداول العديد من أزواج العملات بالتوازي ، فإن التحكيم ممكن أيضًا ، ولكن تسلسل المعاملات سيكون غير بديهي بالفعل. على سبيل المثال ، يمكنك شراء 4 يورو مقابل 5 دولارات ، و 3 جنيهات مقابل 4 يورو ، ثم 6 دولارات مقابل 3 جنيهات. الربح من هذا التسلسل من المعاملات سيكون 1 دولار لكل 5 دولارات مستثمرة.



يمكن تداول مئات أزواج العملات في البورصة ، وتتغير أسعار الصرف باستمرار. من المستحيل بالفعل فهم تسلسل المعاملات الذي سيحقق الربح بدون حل خوارزمي.

الانتقال إلى مشكلة الخوارزمية

تخيل معاملات صرف العملات المحتملة في شكل خوارزمية ، أي في شكل رسم بياني. تمثل القمم في هذا الرسم البياني العملات ، والحواف هي عمليات تداول محتملة. يتوافق طول الضلع مع سعر الصرف الذي يمكن إتمام المعاملة به.


السؤال التالي هو كيفية العثور على سلسلة من المعاملات في مثل هذا العمود الذي سيحقق الربح. من الواضح ، لأنه في بداية التسلسل وفي نهايته يجب أن يكون نفس العملة ، يجب أن يتوافق التسلسل مع الدورة في الرسم البياني المعطى. بعد ذلك ، تحتاج إلى تحديد كيفية حساب سعر الصرف بين العملتين إذا لم يتم تبادلهما مباشرة ، ولكن من خلال عملة ثالثة معينة (أو عدد عشوائي من العمليات الوسيطة). كل شيء هنا بسيط للغاية. سيتم احتساب سعر الصرف هذا على أنه نتاج أسعار الصرف للمعاملات الوسيطة. يصبح التسلسل المربح للمعاملات إذا كان هذا المنتج يأخذ قيمة أقل من واحد. بمعنى آخر ، إذا كان من الممكن شراء وحدة من العملات أقل من وحدة من نفس العملة.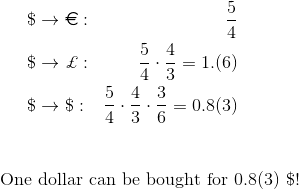


خوارزميات الرسم البياني الكلاسيكي غير مناسبة للعمل مع منتج بأطوال الحواف. هذه الخوارزميات موجهة أساسًا نحو إيجاد مسار يتم تعريفه على أنه مجموع هذه الأطوال. ومع ذلك ، للتغلب على هذا القيد ، هناك طريقة رياضية للانتقال من منتج إلى مبلغ. هذه الطريقة هي اللوغاريتم. إذا ظهر المنتج تحت اللوغاريتم ، فيمكن تحويل هذا اللوغاريتم إلى مجموع اللوغاريتمات. على الجانب الأيمن من هذه المعادلة ، الرقم المطلوب أقل من واحد ، مما يعني أن لوغاريتم هذا الرقم يجب أن يكون أقل من صفر.




تتيح لك هذه الحيلة الرياضية البسيطة الانتقال من البحث عن دورة يكون ناتج أطوال الحواف أقل من واحد إلى إيجاد دورة يقل مجموع أطوال الحواف فيها عن الصفر. تبدو مثل هذه المهمة قابلة للحل بالفعل من خلال خوارزميات الرسم البياني الكلاسيكية ، وبشكل أكثر دقة خوارزمية بلمان-فورد.

Bellman - Ford Algorithm

عادة ما يتم استخدام خوارزمية Bellman-Ford لإيجاد المسافة من قمة معينة إلى جميع القمم الأخرى للرسم البياني ، ولكن تعديلها يسمح بإيجاد دورات ذات طول سالب.

العملية الأساسية لهذه الخوارزمية هي استرخاء الحافة. جوهر هذه العملية على النحو التالي. افترض أن هناك حافة$$$a \rightarrow b$ ، والقيم الأولية المحسوبة سابقًا للمسافات إلى القمم معروفة أيضًا$$$a$ و$$$b$ . لأداء استرخاء الحافة ، من الضروري حساب المسافة إلى القمة$$$b$ إذا كان المسار يمر عبر القمة$$$a$ والضلع$$$a \rightarrow b$ . يتم حساب هذه المسافة كمجموع المسافة إلى القمة.$$$a$ وضلع أطوال$$$a \rightarrow b$ . علاوة على ذلك ، إذا كانت هذه المسافة أقل من المسافة الأولية الحالية إلى$$$a$ ، هذه هي المسافة ذاتها$$$a$ ينمق ويأخذ على القيمة الجديدة تحسب فقط.

بقية الخوارزمية غير معقدة أيضًا. ضروري$$$N$ مرات ($$$N$ هو عدد رؤوس الرسم البياني) تجاوز قائمة الحواف ، وتطبيق عملية استرخاء لكل جولة. يتم الحصول على تعقيد الخوارزمية$$$N*M$ (أين$$$N$ هو عدد القمم و$$$M$ هو عدد الحواف). بالنسبة للرسم البياني بدون دورات سلبية ، لن يؤدي المزيد من استرخاء الحواف إلى تغيير في المسافة إلى القمم. في الوقت نفسه ، بالنسبة للرسم البياني الذي يحتوي على دورة سلبية ، سيقلل الاسترخاء المسافة من القمم وبعدها$$$N$الحلول N. يمكن استخدام هذه الخاصية للعثور على الدورة المطلوبة.

يجب أن يساعد التنفيذ الصغير التالي للخوارزمية الموضحة أعلاه في Kotlin أولئك الذين هم أكثر دراية بفرز التعليمات البرمجية.

fun findNegativeCycle(nodes: Int, edges: Array<Edge>, source: Int): List<Int>? {
    // Initialize distances and prev arrays. All distances but the distance to
    // the source node are infinite, distance to the source node is zero.
    val distances = DoubleArray(nodes) { if (it == source) 0.0 else INFINITY }
    val prev = IntArray(nodes) { -1 }

    // Relax all edges N times where N is the number of nodes.
    repeat(nodes) {
        edges.forEach { it.relax(distances, prev) }
    }

    // Try to relax at least one more edge. If it's possible memorize the node,
    // otherwise return from the method.
    val firstRelaxedEdge = edges.firstOrNull { it.relax(distances, prev) }
    var node = firstRelaxedEdge?.to ?: return null

    // Step back N times where N is the number of nodes. As a result, the node will
    // be in the loop for sure.
    repeat(nodes) {
        node = prev[node]
    }

    // Recover the loop by the node that is inside it and prev links.
    val lastNode = node
    return buildList {
        do {
            add(node)
            node = prev[node]
        } while (node != lastNode)

        reverse()
    }
}

// Edge DTO with implemented relaxation operation.
data class Edge(val from: Int, val to: Int, val length: Double) {

    fun relax(distances: DoubleArray, prev: IntArray): Boolean {
        if (distances[from] + length >= distances[to]) {
            return false
        }

        distances[to] = distances[from] + length
        prev[to] = from
        return true
    }
}

دعونا نفحص مثالاً برسم بياني صغير يتضمن دورة ذات طول سالب. لكي تعمل الخوارزمية ، من الضروري أن تحافظ كل قمة على المسافة الحالية المعروفة لها ، بالإضافة إلى ارتباط إلى القمة السابقة. يتم تحديد الإشارة إلى القمة السابقة في هذه الحالة من خلال الاسترخاء الناجح للضلع. إذا كانت عملية الاسترخاء ناجحة ، وتم تحديث المسافة إلى القمة ، فسيتم أيضًا تحديث الرابط إلى القمة السابقة لهذا الرأس ويأخذ قيمة قمة المصدر للحافة المعطاة.

لذا ، تحتاج أولاً إلى تهيئة القمم من خلال تعيين المسافة إلى جميع القمم باستثناء اللانهاية المتساوية الأولية. بالنسبة للرأس الأولي ، يتم تعيين مسافة صفر.


يتبع الجولة الأولى من جميع الأضلاع ويتم الاسترخاء. لا يعطي كل الاسترخاء تقريبًا أي نتيجة ، باستثناء الاسترخاء في الأضلاع$$$a \rightarrow b$ . استرخاء هذا الضلع يسمح لك بتحديث المسافة إلى$$$b$ .


ويتبع ذلك الجولة الثانية من جميع حواف الرسم البياني والاسترخاء المقابل. هذه المرة ، النتيجة هي استرخاء الأضلاع.$$$b \rightarrow c$ ، وكذلك$$$b \rightarrow d$ . يتم تحديث المسافات إلى القمم.$$$c$ و$$$d$ . وتجدر الإشارة هنا إلى أن النتيجة تعتمد على الترتيب الذي يتم فيه اجتياز الحواف.


في الجولة الثالثة من الأضلاع ، من الممكن الاسترخاء بنجاح بالفعل ثلاثة أضلاع ، وهي الأضلاع $$$\rightarrow d$،$$$d \rightarrow e$ ،$$$d \rightarrow b$ . في هذه الحالة ، عندما تكون الأضلاع مسترخية$$$\rightarrow d$ و$$$d \rightarrow b$ المسافات المسجلة سابقا$$$d$ و$$$b$ ، وكذلك الروابط المقابلة لرؤوس سابقة.


في الجولة الرابعة ، تم الانتهاء من عمليات استرخاء الأضلاع بنجاح. $$$b \rightarrow c$و$$$b \rightarrow a$ . في هذه الحالة ، يتم تحديث قيم المسافات التي تم تسجيلها بالفعل إلى القمم مرة أخرى.$$$a$ و$$$c$ ، بالإضافة إلى الروابط المقابلة للقمم السابقة.


الجولة الخامسة هي الأخيرة. الاسترخاء في الأضلاع خلال هذا المشي$$$\rightarrow d$ ،$$$d \rightarrow b$ ،$$$d \rightarrow e$ . هنا يمكنك أن ترى أن وجود دورة ذات طول سالب يقوم بالفعل بإجراء تعديلات معينة على قيم المسافات إلى القمم.


بعد هذه الجولة ، إذا لم يحتوي الرسم البياني على دورة ذات طول سالب ، فستكتمل الخوارزمية ، لأن استرخاء أي حافة لم يكن ليحدث أي تغييرات. ومع ذلك ، بالنسبة إلى هذا الرسم البياني ، نظرًا لوجود دورة ذات طول سالب ، لا يزال بإمكان المرء العثور على حافة يقوم استرخاءها بتحديث المسافة إلى إحدى القمم.


تم العثور على حافة بتحديث استرخائها المسافة إلى القمة. هذا يؤكد وجود دورة الطول السلبي. الآن أنت بحاجة إلى العثور على هذه الدورة نفسها. من المهم أن تكون القمة ، التي يتم تحديث المسافة إليها الآن ، داخل الدورة وخارجها. في المثال ، هذا هو الجزء العلوي$$$e$ وهي خارج الدورة. بعد ذلك ، تحتاج إلى الرجوع إلى الروابط إلى القمم السابقة ، والتي تم تحديثها بعناية في جميع خطوات الخوارزمية. لضمان الدخول في الدورة ، يجب أن تتراجع$$$N$ رؤوس باستخدام هذه الروابط.

في هذا المثال ، ستكون الانتقالات على النحو التالي:$$$e \rightarrow d \rightarrow c \rightarrow b \rightarrow d \rightarrow c$ . لذلك يقع الجزء العلوي$$$c$ ، وهو مكفول في دورة بطول سلبي.


مزيد من مسألة التكنولوجيا. لإرجاع الدورة المطلوبة ، تحتاج إلى التكرار مرة أخرى باستخدام الروابط إلى القمم السابقة حتى يلتقي الرأس مرة أخرى$$$c$ . هذا يعني أن الدورة قد أغلقت. كل ما تبقى هو عكس الترتيب ، حيث تم عكس التكرار أثناء التكرار على الروابط إلى القمم السابقة.

تفترض الخوارزمية أعلاه وجود بعض الذروة الأولية التي يتم حساب المسافات منها. إن وجود مثل هذا الرأس ليس ضروريًا لكي تعمل الخوارزمية ، ولكن تم تقديمها إلى حد أكبر لتتناسب مع خوارزمية Bellman - Ford الأصلية. إذا كان موضوع الاهتمام عبارة عن دورة ذات طول سالب ، فيمكننا أن نفترض أن جميع رؤوس رسم بياني معين أولية. وبعبارة أخرى ، فإن المسافة إلى جميع القمم هي في البداية صفر.

استنتاج

يعد استخدام خوارزمية Bellman-Ford في مشكلة تجارة المراجحة مثالًا ممتازًا على الكيفية التي يمكن بها للخوارزميات الكلاسيكية حل مشاكل العمل الحقيقية ، على وجه الخصوص ، في المجال المالي. التعقيد المقارب للخوارزمية ، يساوي$$$N^3$قد يتبين أن N 3 للرسم البياني المتصل بالكامل كبير جدًا. هذا حقا يجب تذكره. ومع ذلك ، في العديد من الحالات ، مثل صرف العملات ، لا يخلق هذا التعقيد أي مشاكل بسببالعددالصغير نسبيًامن العقدفي الرسم البياني.