👩🏼‍🚒 👩🏽‍🤝‍👨🏻 👆🏾 تصور خطوط التوتر وحركات الشحنات الكهربائية ومحاكاة الحركة الكوكبية للنظام الشمسي 🧙🏻 👩🏽‍🚀 ✋🏽

مرحبًا ، أريد اليوم أن أقدم لك مساعدة بصرية لنمذجة بعض العمليات البدنية وإظهار كيفية الحصول على صور ورسوم متحركة جميلة. احذر الكثير من الصور.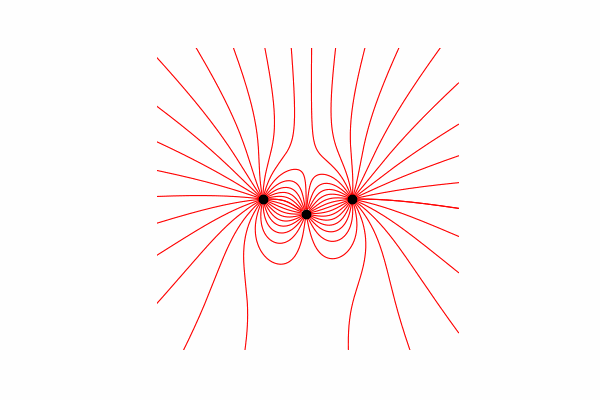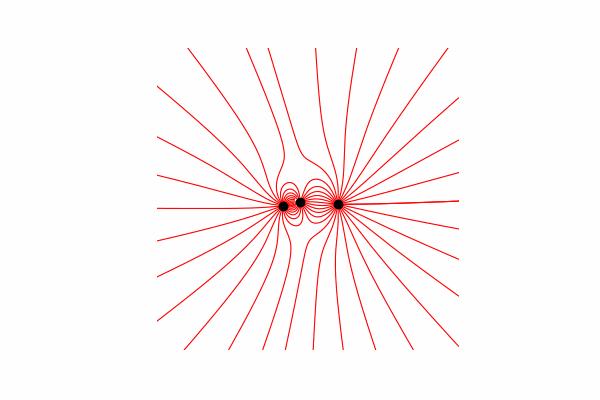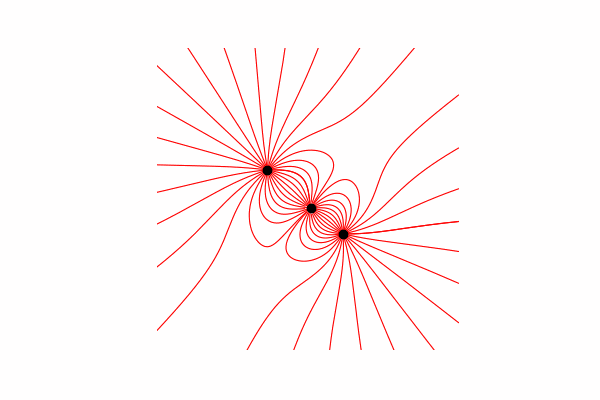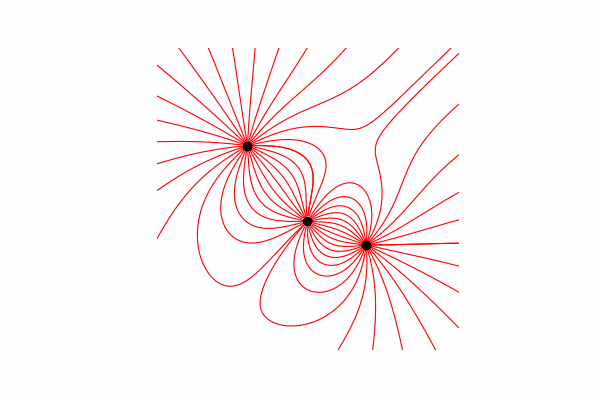

يمكن العثور على جميع التعليمات البرمجية في جوجل كولاب .

نظرية

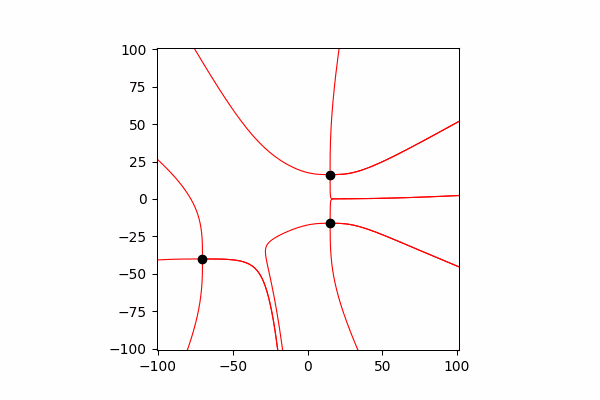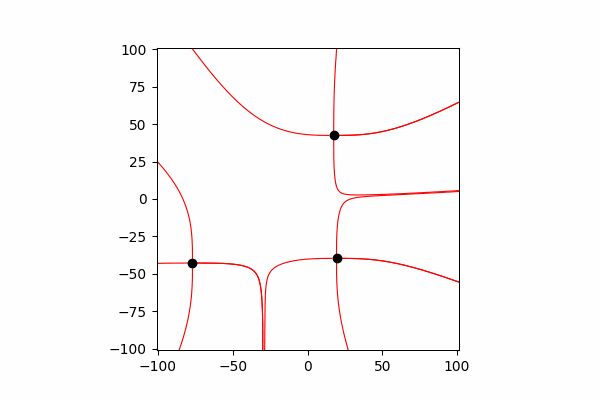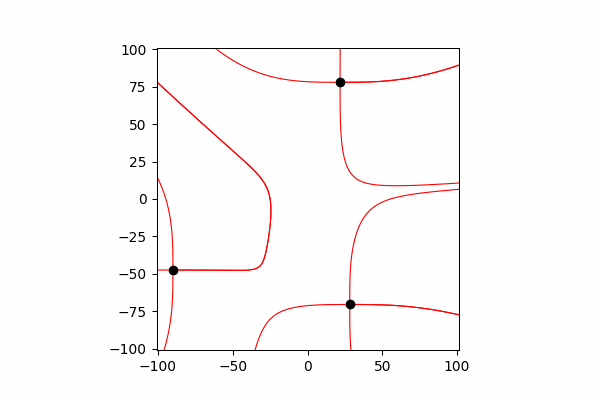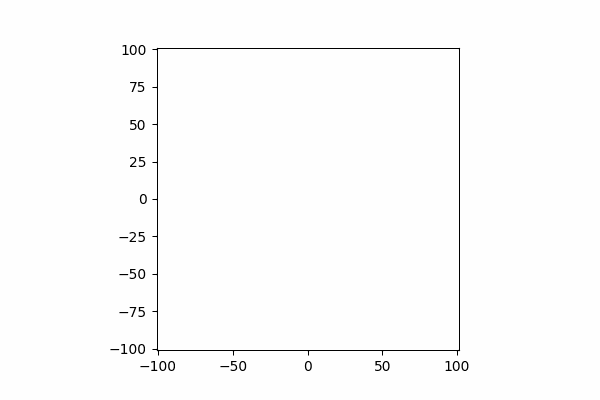
أولاً ، نحتاج إلى حد أدنى نظريًا صغيرًا حول هذا الموضوع. لنبدأ بفهم خطوط التوتر وكيفية حسابها. في الواقع ، هذه الخطوط هي دمج العديد من نواقل التوتر ، والتي يمكن حسابها على النحو التالي: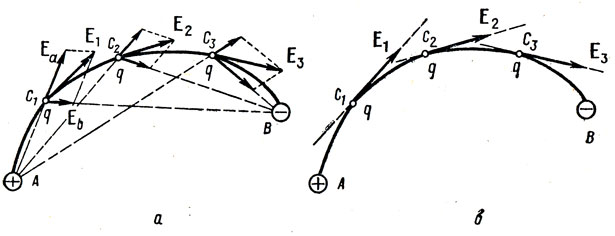

E = \frac{k * | q |}{r^{2}}

$E=\frac{k*|q|}{r^2}$ .

طريقة الحساب E

قمت بحساب متجه التوتر من خلال تشابه المثلثات ، وبالتالي الحصول على إسقاطات على محوري x و y dx و dy ، على التوالي.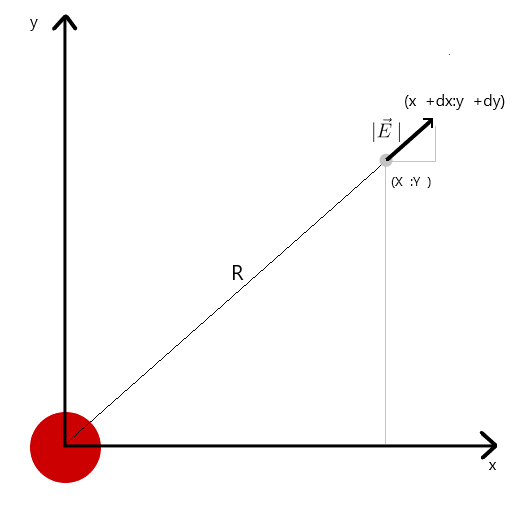

من التشابه يستتبع ذلك أن نصف قطر المتجه من الشحنة إلى النقطة في الفضاء r وطول متجه الشدة E يساوي نسبة إسقاطات هذه المتجهات (x1 و dx ، على التوالي)

\frac{R}{E} = \frac{x}{d x} = \frac{y}{d y}

$\frac{R}{E}=\frac{x}{dx}=\frac{y}{dy}$ . صيغة المتجه الناتج

\vec{E} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{E}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{E}}_{i} |}{R_{i}} \end{matrix})

$\vec{E}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{E}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{E}_i|}{R_i} \end{array}\right) \qquad$
مع هذه المعرفة نحصل على النتيجة الأولى.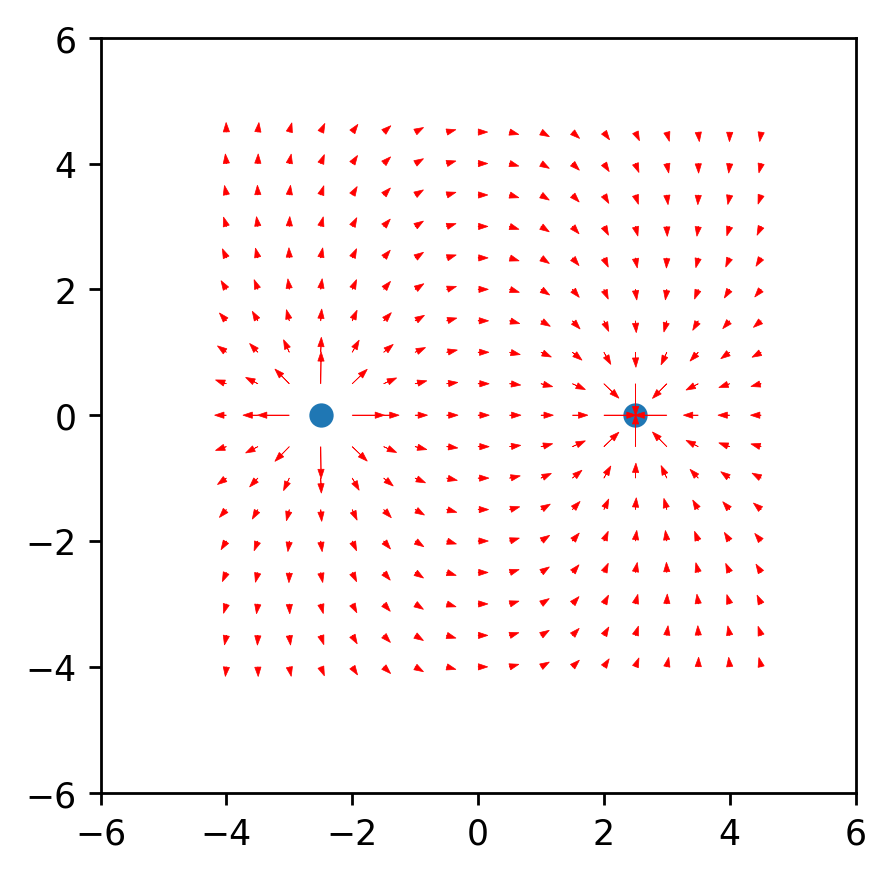

دالة حساب الإسقاط

def E(q_prop, xs, ys, nq): #q_prop=[[xq1, yq1, q1, mq1, vxq1, vyq1], [xq2, yq2, q2, mq2, vxq2, vyq2] ... ] 
    l=1
    k=9*10**9
    Ex=0
    Ey=0
    c=0
    for c in range(len(q_prop)):#                
        q=q_prop[c]
        r=((xs-q[0])**2+(ys-q[1])**2)**0.5
        dEv=(k*q[2])/r**2
        dEx=(xs-q[0])*(dEv/r)*l
        dEy=(ys-q[1])*(dEv/r)*l

        Ex+=dEx
        Ey+=dEy
    return Ex, Ey

طريقة بناء الخط

تحتاج أولاً إلى تحديد نقطة البداية والنهاية من أين سيذهب الخط والمستند. البداية هي نقاط على دائرة نصف قطرها r حول الشحنة ، ونقاط النهاية لا تزيد عن r بصرف النظر عن الشحنات.

رمز لنقاط البداية

theta = np.linspace(0, 2*np.pi, n)
mask=q_prop[ q_prop[:,2]>0 ]#    
for cq in range(len(mask)):
    qmask=mask[cq]
    xr = r_q*np.cos(theta)+qmask[0]# -    
    yr = r_q*np.sin(theta)+qmask[1]#

لذا يجدر القول أن الخطوط مبنية فقط من الشحنات الإيجابية.

وأخيرا ، بناء الخطوط. للقيام بذلك ، نقوم ببناء خط متجه التوتر فيه من نقطة البداية ، وتحديث نقطة البداية في نهاية الخط المبني وتكرارها حتى يتم الوصول إلى شروط النهاية المذكورة أعلاه.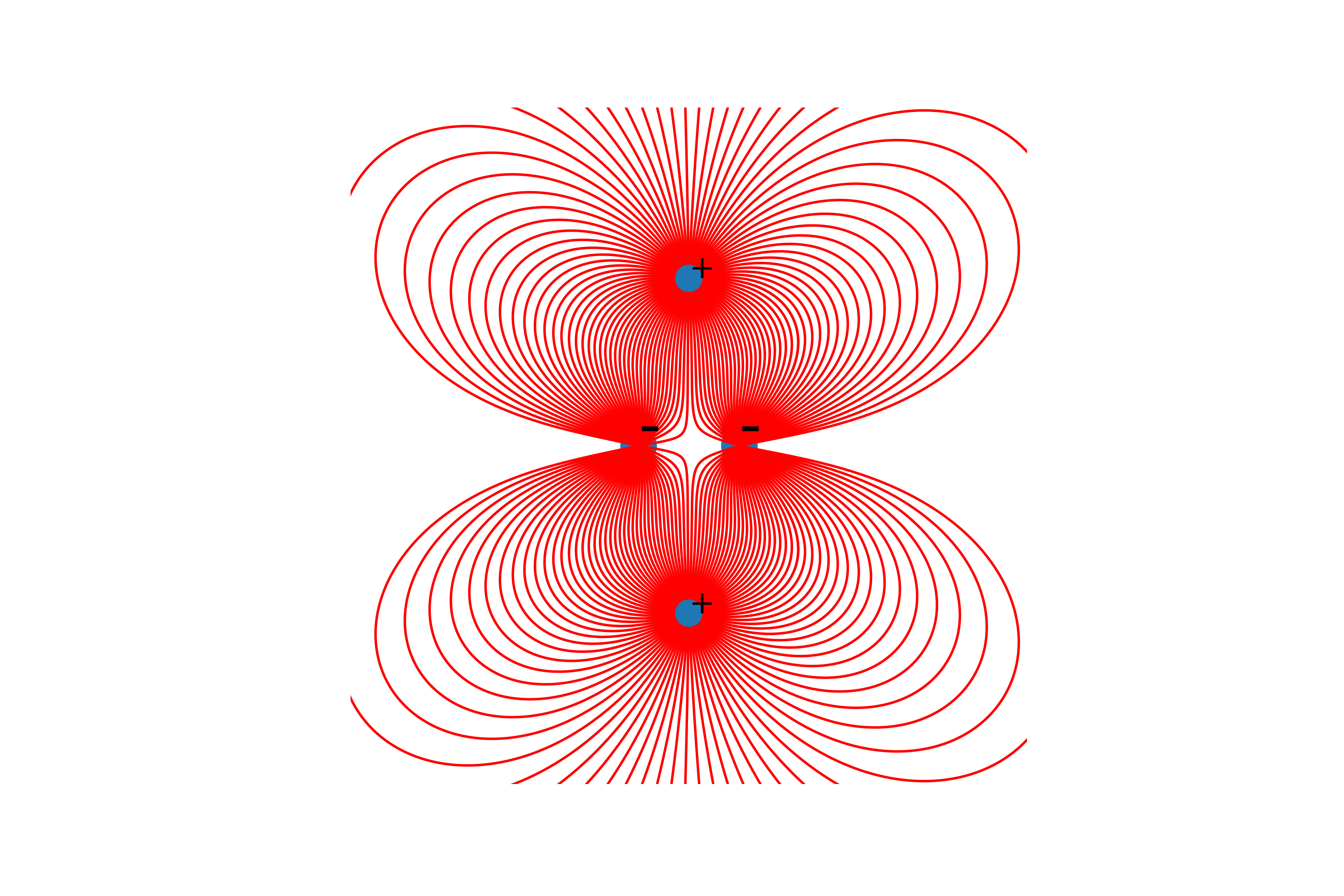

وظيفة حساب تنسيق خط

def Draw(size, q_prop,r_q, n):
  
  linen=np.empty((np.count_nonzero(q_prop[:,2]>0),n, 2000000), dtype=np.float64)
  linen[:] = np.nan
  theta = np.linspace(0, 2*np.pi, n)
  mask=q_prop[ q_prop[:,2]>0 ][ q_prop[q_prop[:,2]>0][:,3]==1 ]
  for cq in range(len(mask)):
    qmask=mask[cq]
    x11 = r_q*np.cos(theta)+qmask[0]
    x22 = r_q*np.sin(theta)+qmask[1]
    for c in range(len(x11)):

      xs=x11[c]
      ys=x22[c]

      lines=np.empty((2,1000000), dtype=np.float64)
      lines[:]=np.nan
      stop=0
      nnn=0
      
      lines[0][nnn]=xs
      lines[1][nnn]=ys
      while  abs(xs)<size+2 and abs(ys)<size+2: 
        nnn+=1

        for cq1 in range(len(q_prop)):
          q=q_prop[cq1]
          if ((ys-q[1])**2+(xs-q[0])**2)**0.5<r_q/2 :
            stop=1
            break
        if stop==1:
          break
        dx, dy = E1(q_prop,xs,ys)

        xs+=dx
        ys+=dy
        lines[0][nnn]=xs
        lines[1][nnn]=ys
       
      linen[cq,c,:]=lines.reshape(-1)

  return linen

التفاعل بين الشحنات

لتعكس تفاعلها ، من الضروري تغيير إحداثياتها وسرعتها بعد كل وقت صغير dt.

x + = \frac{E_{x} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{x} \cdot d t

$x+=\frac{E_x \cdot q \cdot dt^2}{2\cdot m} + v_x\cdot dt$

y + = \frac{E_{y} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{y} \cdot d t

$y+=\frac{E_y \cdot q \cdot dt^2}{2\cdot m} + v_y \cdot dt$

v_{x} + = \frac{E_{x} \cdot q \cdot d t}{m}

$v_x+= \frac{E_x \cdot q \cdot dt}{ m}$

v_{y} + = \frac{E_{y} \cdot q \cdot d t}{m}

$v_y+= \frac{E_y \cdot q \cdot dt}{ m}$

وظيفة لتحديث الإحداثيات وتوقعات سرعات الشحن

def Update_all(q_prop):
  vx=0
  vy=0
  x=0
  y=0
  q_prop_1=np.copy(q_prop)
  for c in range(len(q_prop)):#         
    xs=q_prop[c][0]
    ys=q_prop[c][1]
    q =q_prop[c][2]
    m =q_prop[c][3]
    vx=q_prop[c][4]
    vy=q_prop[c][5]
    Ex, Ey= E(q_prop, xs, ys, c)

    x=(((Ex*q)/m)*dt**2)/2+vx*dt+xs
    y=(((Ey*q)/m)*dt**2)/2+vy*dt+ys
    vx+=((Ex*q)/m)*dt
    vy+=((Ey*q)/m)*dt
    #print(q_prop[c]-[x,y,q,m,vx,vy])
    q_prop_1[c]=[x,y,q,m,vx,vy]
  
  return q_prop_1#

الجاذبية

بناءً على الكود الحالي ، كتبت محاكيًا يعكس تحركات الأجسام تحت تأثير الجاذبية. التغييرات في الكود هي أساسا لوظيفة التوتر منذ ذلك الحين سيتم النظر في التسارع الآن باستخدام صيغة مماثلة.

g = \frac{G * m}{r^{2}}

$g=\frac{G*m}{r^2}$

\vec{g} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{g}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{g}}_{i} |}{R_{i}} \end{matrix})

$\vec{g}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{g}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{g}_i|}{R_i} \end{array}\right) \qquad$

تبدأ الكواكب من المحور x على مسافة الحضيض وبسرعة الحضيض. جميع قيم الكواكب والشمس (الكتلة والمسافة والأطراف) من الدليل.

رسوم متحركة لأول 4 كواكب + شمس.

في انتظار النقد والاقتراحات. وداعا.

تصور خطوط التوتر وحركات الشحنات الكهربائية ومحاكاة الحركة الكوكبية للنظام الشمسي

نظرية

طريقة الحساب E

طريقة بناء الخط

التفاعل بين الشحنات

الجاذبية

More articles: